n元非齐次线性方程组及其解法
【主要内容】
1.n元非齐次线性方程组的概念
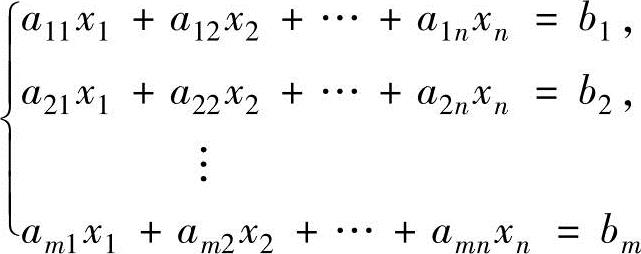
(其中,b1,b2,…,bm是不全为零的常数,称为该方程组的常数项)称为n元非齐次线性方程组,记

则上述方程组可简记为Ax=b.(Ⅰ)
称满足式(Ⅰ)的x为该方程组的解或解向量.称与式(Ⅰ)对应的齐次线性方程组Ax=0(Ⅱ)
(其中,0是m维零(列)向量)为方程组(Ⅰ)的导出组.
非齐次线性方程组解的性质:
(1)设η1,η2都是方程组(Ⅰ)的解,则η1-η2是方程组(Ⅱ)的解.
(2)设ξ是方程组(Ⅰ)的特解,η是方程组(Ⅱ)的解,则ξ+η是方程组(Ⅰ)的解.
2.n元非齐次线性方程组有解的充分必要条件
方程组(Ⅰ)有无穷多解的充分必要条件为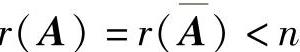 (其中,
(其中,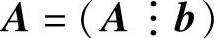 称为方程
称为方程
组(Ⅰ)的增广矩阵).
方程组(Ⅰ)有唯一解的充分必要条件为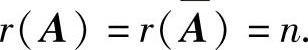
方程组(Ⅰ)无解的充分必要条件为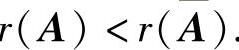
3.非齐次线性方程组的通解
当r(A)=r(A)<n时,方程组(Ⅰ)有无穷多解,这时它的通解为
x=c1ξ1+c2ξ2+…+cn-rξn-r+η,其中,ξ1,ξ2,…,ξn-r(r=r(A))是导出组(Ⅱ)的一个基础解系,η是方程组(Ⅰ)的一个特解.
注 设A是n阶可逆矩阵,记其行列式为D,则方程组Ax=b有唯一解,x=A-1b,
即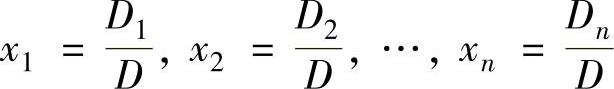 ,
,
其中,Di是D的第i列用b代替后的行列式(i=1,2,…,n)(以上称为克莱姆法则).
【典型例题】
例6.2.1 (单项选择题)设非齐次线性方程组Ax=b(其中,A是m×n矩阵),记r(A)=r,则( ).
A.r=m时,Ax=b有解 B.r=n时,Ax=b有唯一解
C.m=n时,Ax=b有唯一解 D.r<n时,Ax=b有无穷多解
精解 考虑非齐次线性方程组Ax=b的有解问题时,首先应考虑r(A)=r(A)是否成立.当r=m时,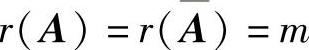 ,所以Ax=b有解.
,所以Ax=b有解.
因此本题选A.
例6.2.2 (单项选择题)设α1,α2,α3是四元非齐次线性方程组Ax=b的三个解向量,且r(A)=3,α1=(1,2,3,4)T,α2+α3=(0,1,2,5)T,k为任意常数,则Ax=b的通解x=( ).
A.α1+k(1,1,1,1)T B.α1+k(α2+α3)
C.α1+k(2,3,4,3)T D.α1+k(3,4,5,6)T
精解 由r(A)=3知,Ax=b的导出组Ax=0的基础解系只含有一个解向量,可以取为
2α1-(α2+α3)=(2,3,4,3)T,所以,Ax=b的通解为
x=α1+k(2,3,4,3)T.
因此本题选C.
例6.2.3 已知β1,β2是非齐次线性方程组Ax=b的两个不同的解,α1,α2是对应的导出组Ax=0的一个基础解系,k1,k2是任意常数,则方程组Ax=b的通解是().A.
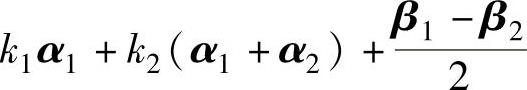 B.
B.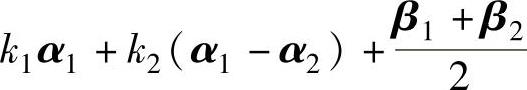
C.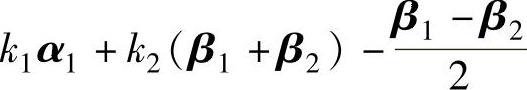 D.
D.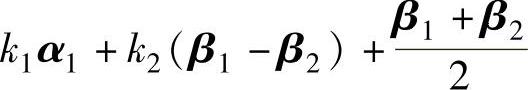
精解 首先指出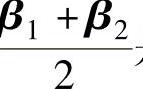 是Ax=b的一个特解,此外,α1,α1-α2都是Ax=0的解,且
是Ax=b的一个特解,此外,α1,α1-α2都是Ax=0的解,且
它们线性无关,所以也是Ax=0的一个基础解系.从而Ax=b的通解为
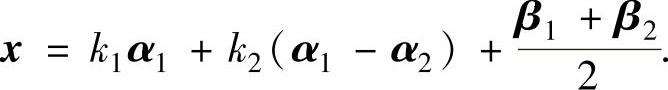
因此本题选B.(https://www.daowen.com)
例6.2.4 设非齐次线性方程组
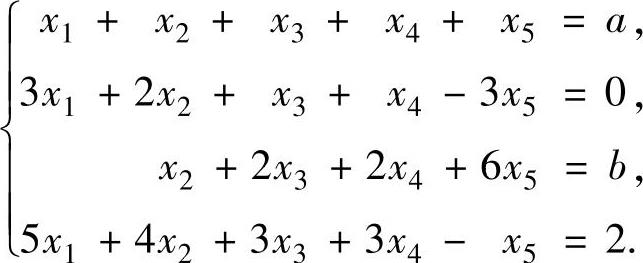
(1)问a,b为何值时,方程组有解;
(2)方程组有解时,求出它的通解.
精解 (1)所给方程组的增广矩阵为

由此可知,当a,b满足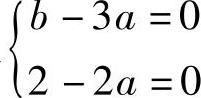
,
{,即a=1,b=3时,所给方程组的增广矩阵与系数矩阵有
相同的秩2,此时此方程组有解(有无穷多解).
(2)当a=1,b=3时,所给方程组的增广矩阵

所以,此时原方程组与方程组
同解.
方程组(1)的导出组
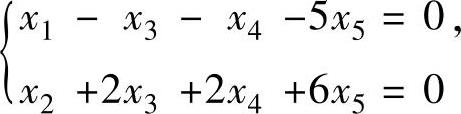
有3个自由未知数,取为x3,x4,x5,对它们赋值为1,0,0;0,1,0;0,0,1得该导出组的基础解系为
(1,-2,1,0,0)T,(1,-2,0,1,0)T,(5,-6,0,0,1)T.
此外方程组(1)有特解(-2,3,0,0,0)T.所以原方程组的通解为
(x1,x2,x3,x4,x5)T=(-2,3,0,0,0)T+c1(1,-2,1,0,0)T+
c2(1,-2,0,1,0)T+c3(5,-6,0,0,1)T.
例6.2.5 已知非齐次线性方程组
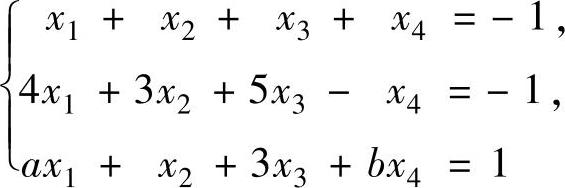
有3个线性无关的解.
(1)证明:方程组系数矩阵A的秩r(A)=2;
(2)求常数a,b的值及方程组的通解.
精解 (1)设三个线性无关的解为α1,α2,α3,则α1-α2,α1-α3是所给方程组的导出组Ax=0的两个线性无关解,所以Ax=0的基础解系中至少包含两个解向量,由此得到
4-r(A)≥2,即 r(A)≤2.(1)
另外,由所给方程组r(A)≥2.(2)
由式(1)与式(2)得 r(A)=2.
(2)由于
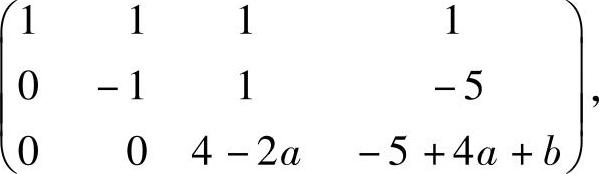
所以,由r(A)=2得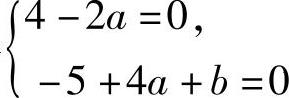 {, 即a=2,b=-3.将它们代入所给方程组的增广矩阵得
{, 即a=2,b=-3.将它们代入所给方程组的增广矩阵得
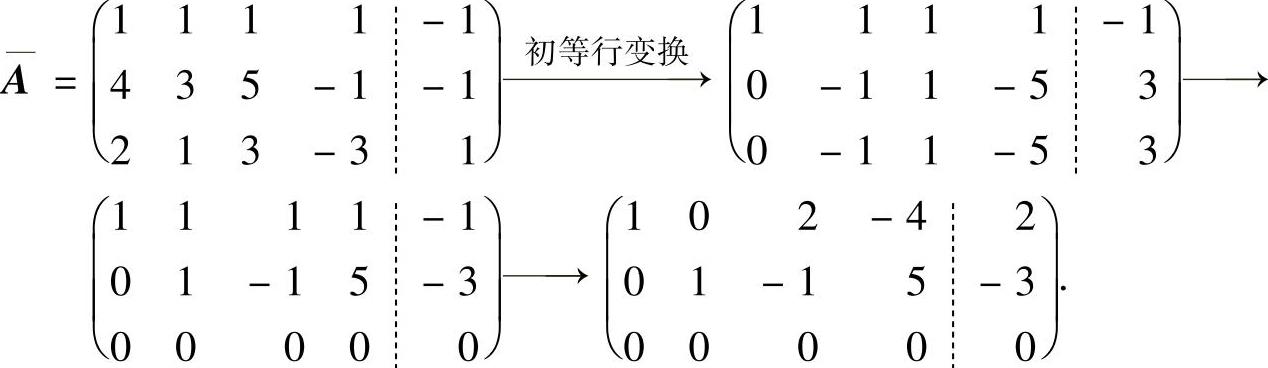
由此可知,当a=2,b=-3时,所给方程组与方程组

同解.
方程组(3)的导出组
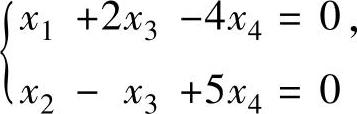
有两个自由未知数,取为x3,x4,并赋值为1,0与0,1,于是该导出组的基础解系为
(-2,1,1,0)T,(4,-5,0,1)T.此外方程组(3)有特解(2,-3,0,0)T.所以原方程组的通解为
x=c1(-2,1,1,0)T+c2(4,-5,0,1)T+(2,-3,0,0)T.
