二元函数极限与连续的概念、偏导数及二阶偏导数的计算
【主要内容】
1.二元函数极限与连续的概念
设二元函数f（x，y）在点（x0，y0）的某个去心邻域{（x，y）|0<（x-x0）2+（y-y0）2<δ2}（其中，δ是某正数）内有定义.如果动点（x，y）以任何方式无限趋于点（x0，y0）时，f（x，y）总是无限趋于常数A，则称A是点（x，y）趋于点（x0，y0）（记为（x，y）→（x0，y0））时f（x，y）的极限，记为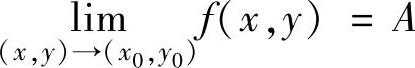
或
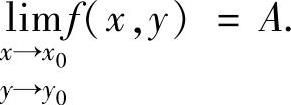
注 根据定义，可以按以下方法判定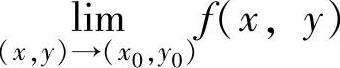
是否存在：
（ⅰ）如果点（x，y）按某种方式趋于点（x0，y0）时，f（x，y）不趋于任一值，则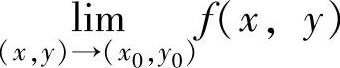
不存在；
（ⅱ）如果点（x，y）按某两种方式趋于点（x0，y0）时，f（x，y）趋于两个不同值，则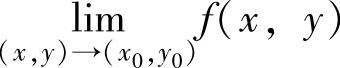
不存在.
设二元函数f（x，y）在点（x0，y0）的某个邻域内有定义.如果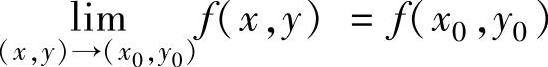
，则称f（x，y）在点（x0，y0）处连续.
如果f（x，y）在区域D的每一点处都连续，则称f（x，y）在区域D上连续.
注 当f（x，y）是有界闭区域D上的连续函数时，它有以下性质：
（ⅰ）f（x，y）在D上必有最大值和最小值，即在D上存在点（x0，y0）和（x1，y1），使得
f（x0，y0）=M（f（x，y）在D上的最大值），f（x1，y1）=m（f（x，y）在D上的最小值）
（ⅱ）f（x，y）可以取到其在D上的最小值m和最大值M之间的任何值C，即存在（ξ，η）∈D，使得f（ξ，η）=C.
2.二元函数偏导数的定义与计算
设二元函数f（x，y）在点（x0，y0）的某个邻域内有定义.如果极限
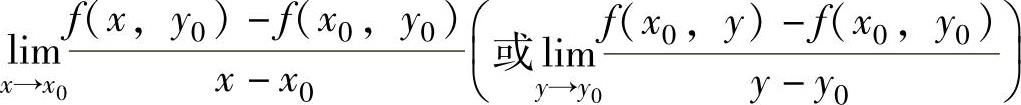
存在，则称这个极限值为f（x，y）对x（或y）的偏导数，记为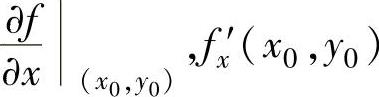
（或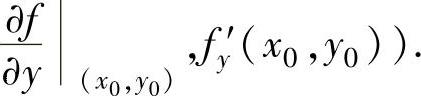
根据定义，fx′（x0，y0）与fy′（x0，y0）可分别通过计算函数f（x，y0）在点x0处的导数与函数f（x0，y）在点y0处的导数得到.
注 当（x，y）是区域D上的任一点时，f（x，y）在该点对x（或对y）的偏导数为fx′（x，y）简记fx′，或
称为偏导函数（简称偏导数），它们往往是关于x，y的二元函数.
3.二元函数二阶偏导数的定义与计算
设二元函数f（x，y）的偏导函数fx′（x，y），fy′（x，y）在点（x0，y0）仍有偏导数，则称这些偏导数为f（x，y）在点（x0，y0）的二阶偏导数，记为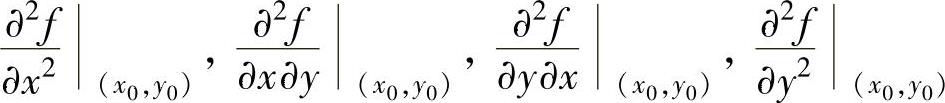
，或对应地记为fx″x（x0，y0），fx″y（x0，y0），fy″x（x0，y0），fy″y（x0，y0）.
根据定义，fx″x（x0，y0）可以通过计算f（x，y0）在点x0处的二阶导数得到，fy″y（x0，y0）可以通过计算f（x0，y）在点y0处的二阶导数得到，而fx″y（x0，y0）可以通过计算fx′（x0，y）在点y0处的导数得到，fy″x（x0，y0）可以通过计算fy′（x，y0）在点x0处的导数得到.
如果函数f（x，y）在区域D的任一点（x，y）处都有二阶偏导数，则记为
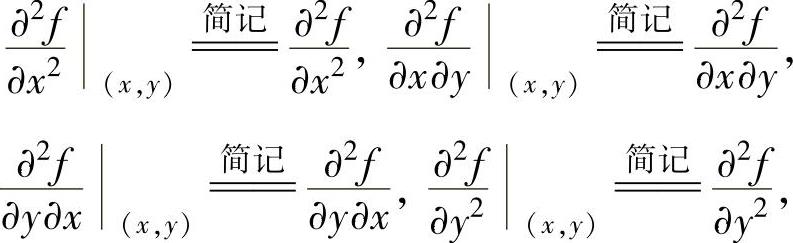
或相应地记为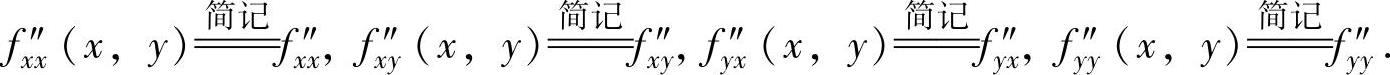
显然，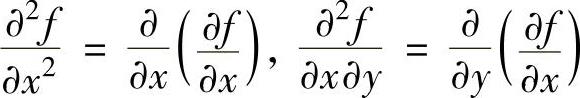
，
，
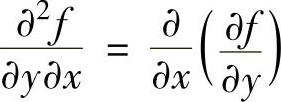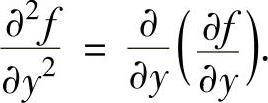
注 （ⅰ）设函数f（x，y）的两个二阶混合偏导数fx″y，fy″x在点（x0，y0）处（在区域D）连续，则在点（x0，y0）（在区域D）有fx″y=fy″x.
（ⅱ）f（x，y）的三阶、四阶偏导数也可用类似方法定义.(https://www.daowen.com)
【典型例题】
例3.1.1 设二元函数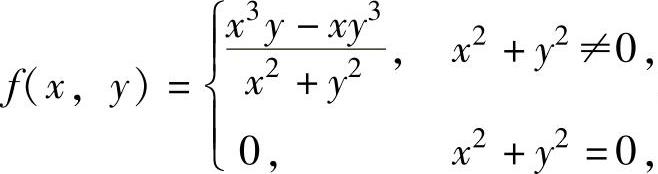
求fx′（0，0）和fx″y（0，0）.
精解 先由偏导数定义计算出fx′（0，0）和fx′（0，y）（y≠0），然后再由偏导数定义计算fx″y（0，0）.
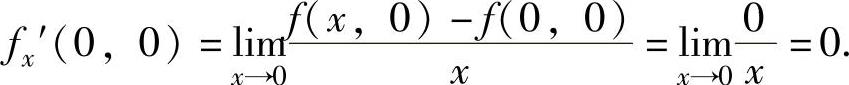
此外，由于y≠0时，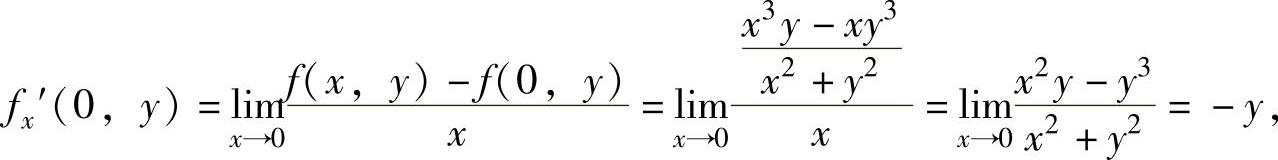
所以，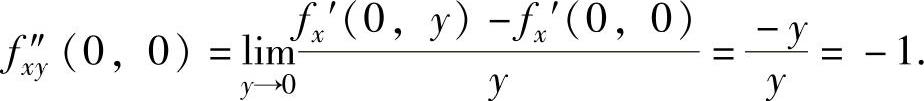
例3.1.2 设二元函数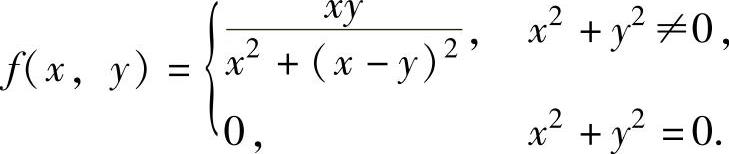
（1）求fx′（0，0），fy′（0，0）；
（2）讨论fx′（x，y）在点（0，0）处的连续性.
精解 （1）按定义计算fx′（0，0）和fy′（0，0）.
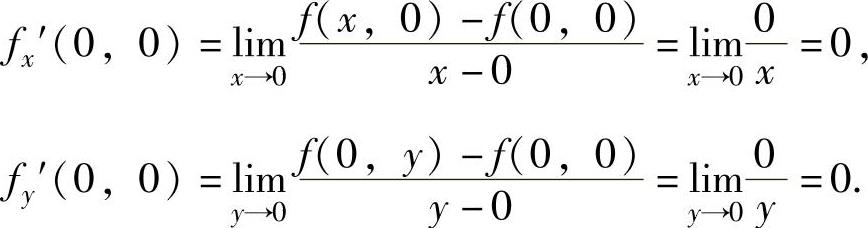
（2）当x2+y2≠0时，
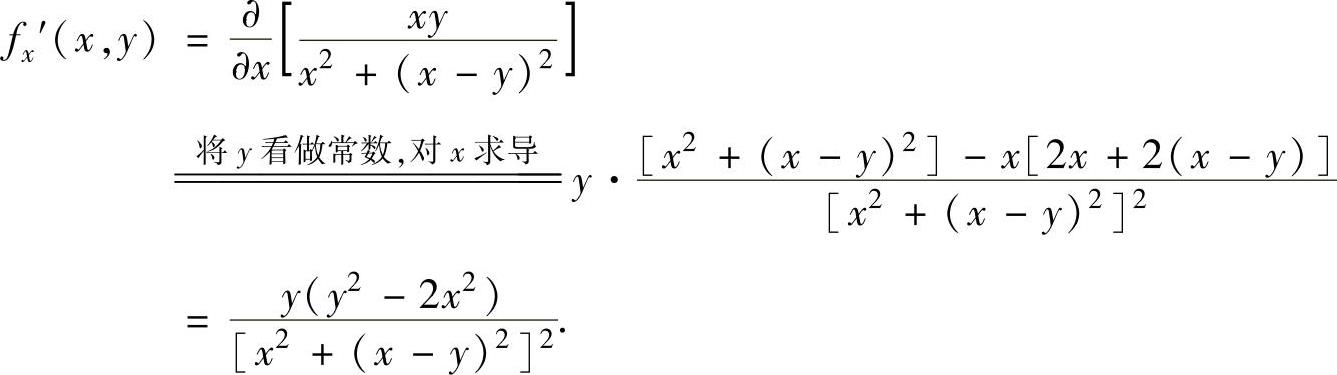
所以，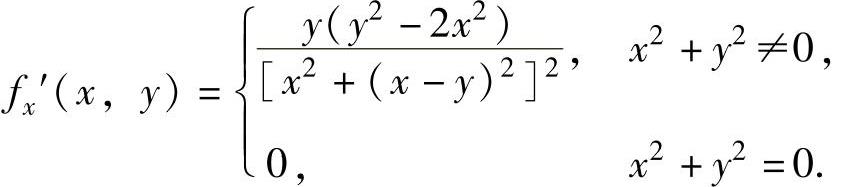
由于，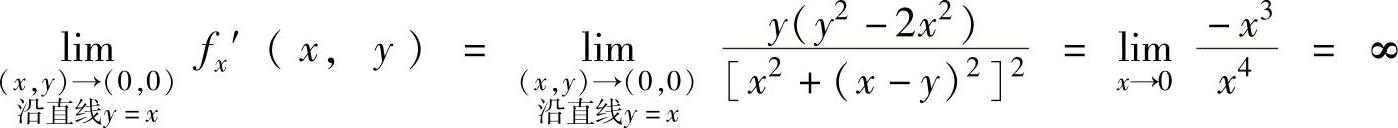
，即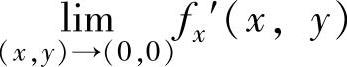
不存在，所以fx′（x，y）在点（0，0）处不连续.
例3.1.3 设z=yx+xy.求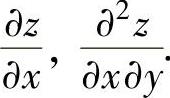
精解 先分别计算z1=yx，z2=xy的一阶和二阶偏导数：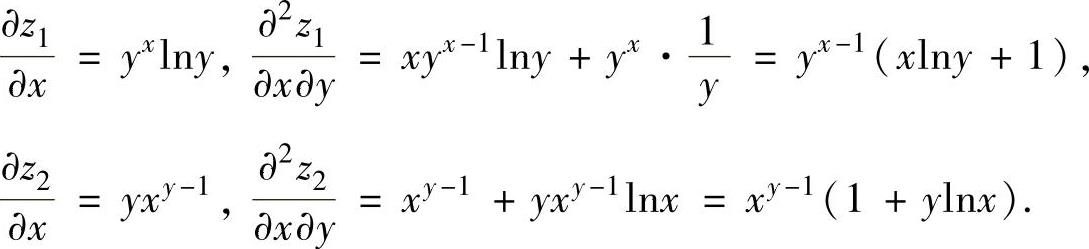
所以，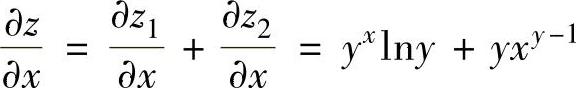
，
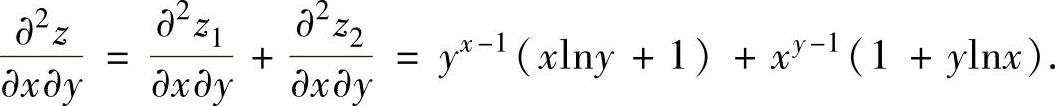
例3.1.4 设二元函数f（x，y）满足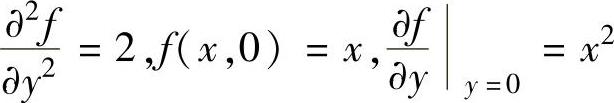
，求f（x，y）的表达式.
精解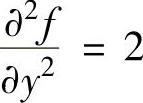
的两边对y积分（此时将x看做常数）得
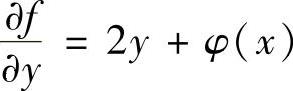（其中，φ（x）是关于x的待定函数）.（1）
在式（1）中，令y=0，则由题设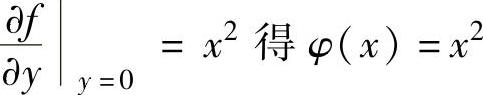
，将它代入式（1）得
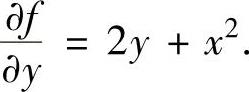
上式两边对y积分（此时将x看做常数）得
f（x，y）=y2+x2y+ψ（x）（其中，ψ（x）是关于x的待定函数）.（2）在式（2）中令y=0，则由题设f（x，0）=x得ψ（x）=x.将它代入式（2）得
f（x，y）=y2+x2y+x.
注 对一元函数f（y）来说，由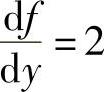
得f（y）=2y+C（其中，C是任意常数），但对二元
函数f（x，y）来说，由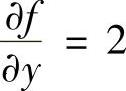
得f（x，y）=2y+φ（x）（其中，φ（x）是关于x的任意函数）.