练习题五解答

练习题五解答

1.单项选择题

（1）D （2）C （3）B （4）C （5）D （6）C

（7）A （8）C （9）C （10）A （11）B （12）C

（13）B （14）D （15）B （16）D （17）D （18）A

（19）A （20）A （21）C （22）D （23）B （24）D

（25）B （26）C （27）B （28）B （29）C （30）D

2.解答题

（2）

（3）

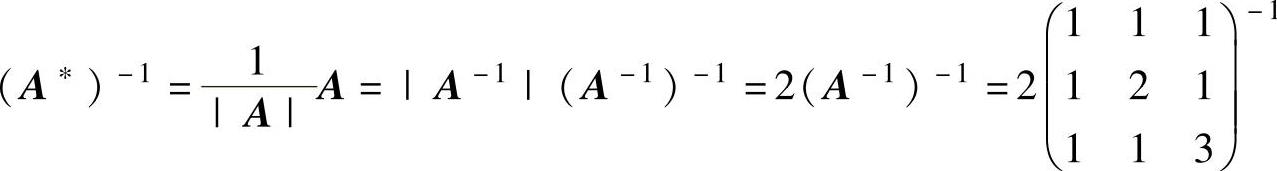
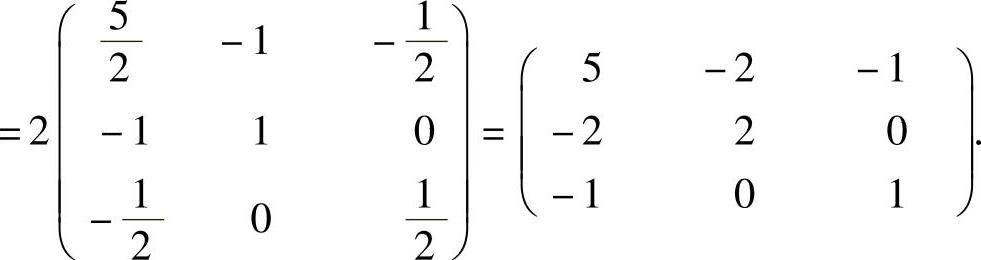
（4）由ABA^-1=BA^-1+3E₄得A∗ABA^-1A=A∗BA^-1A+3A∗A，即|A|B=A∗B+3|A|E_4.由|A|³=|A∗|=8得|A|=2.所以上式成为

（2E₄-A∗）B=6E₄，即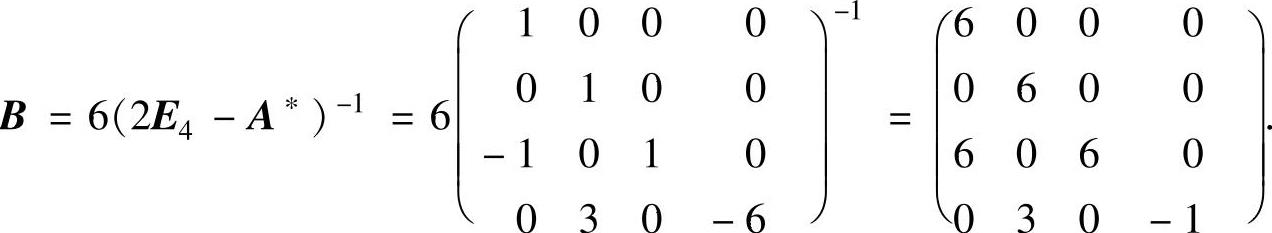

（5）由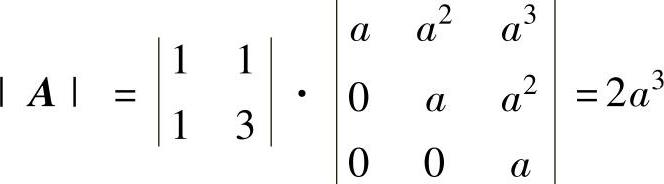知，A可逆的充分必要条件是a≠0.当a≠0时，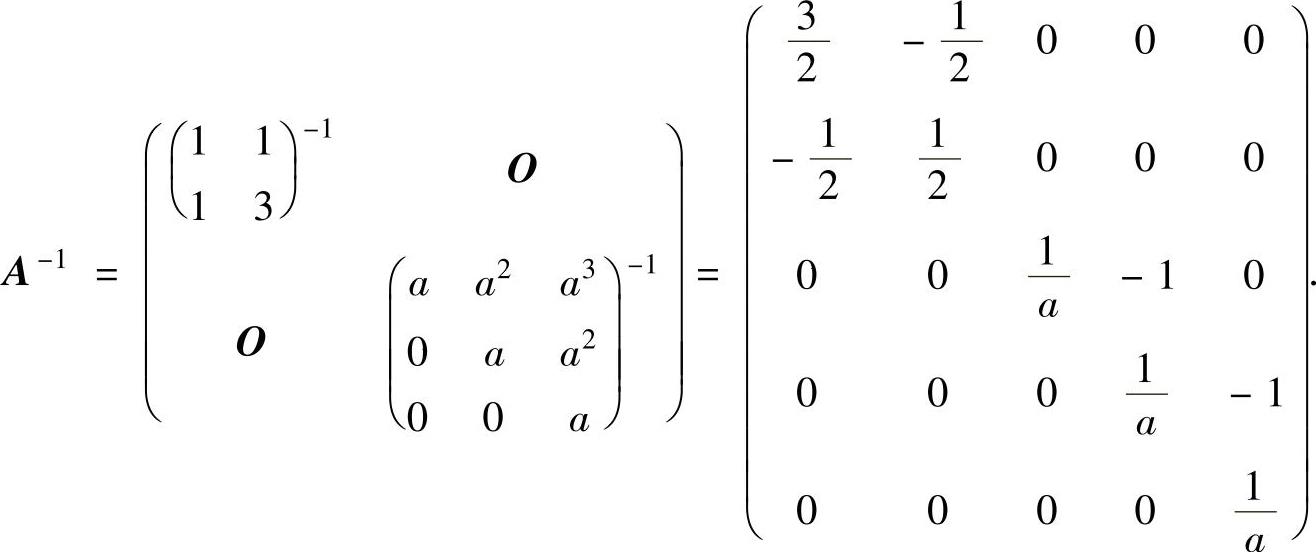

（6）由ABA∗=2BA∗+E₃得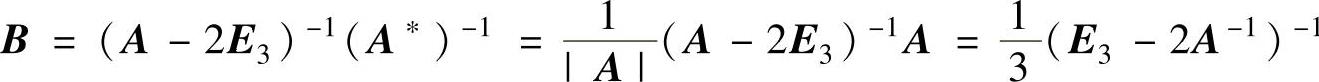（由于|A|=3），

即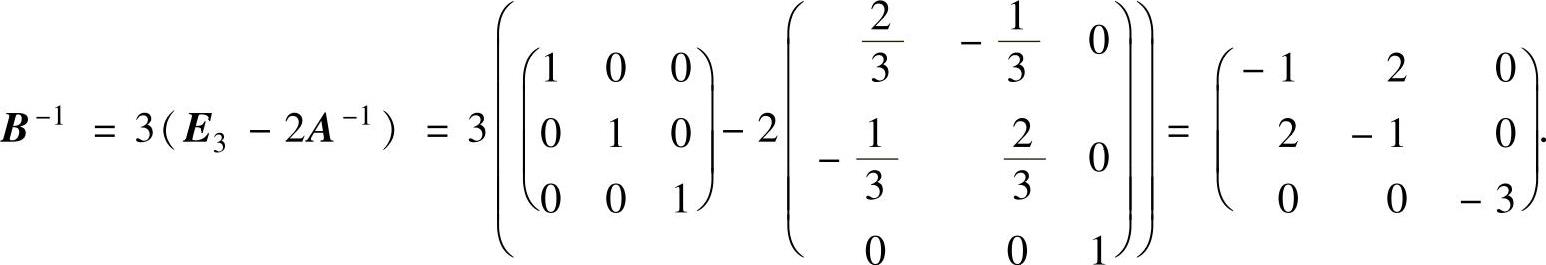

从而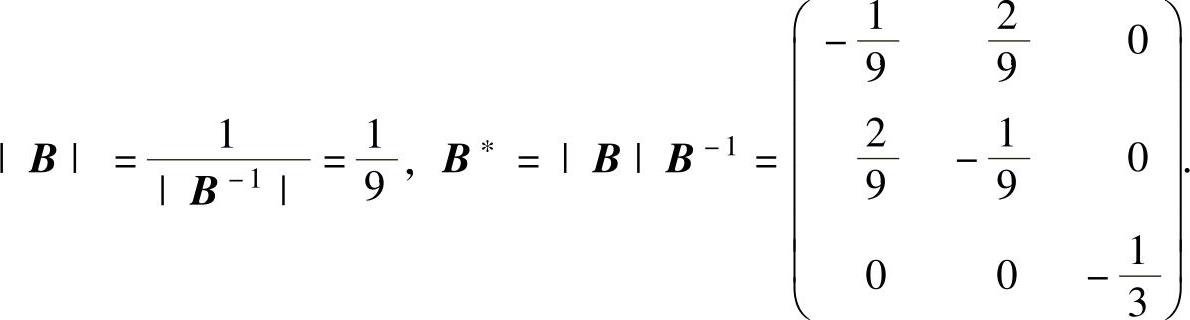

（7）Aⁿ-2A^n-1=A^n-2·A（A-2E₃）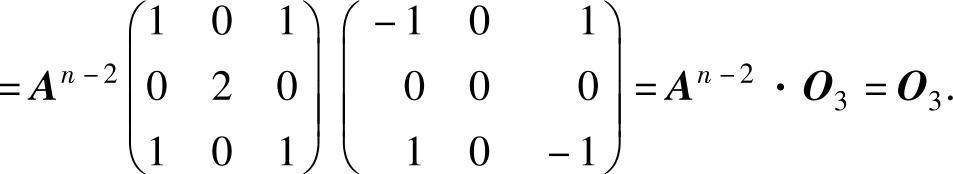

（8）由AB=E_n，即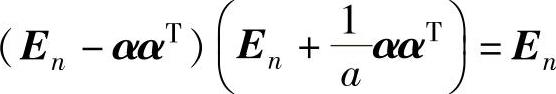得（2a²+a-1）αα^T=O_n由αα^T≠On

得2a²+a-1=0，由此得a=-1.

（9）（ⅰ）由2A^-1B=B-4E₃得AB-2B-4A=O₃，即（AB-2B）-（4A-8E₃）=8E_3.于是有

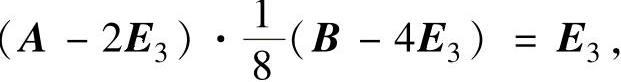
所以，A-2E₃可逆.

（ⅱ）由（ⅰ）得

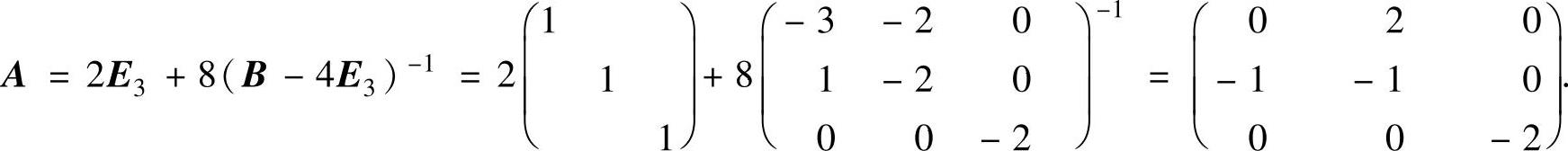
（10）由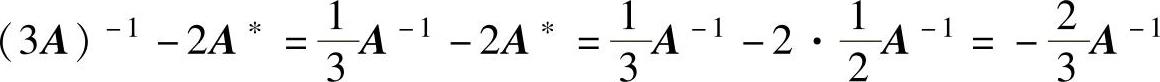得

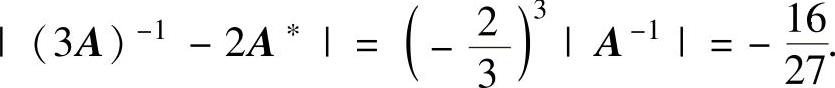
（11）由于|B|=10，即B可逆，所以r（AB）=r（A）=2.

（12）（ⅰ）由AB=O₃得r（A）+r（B）-3≤r（AB）=0，即r（A）+r（B）≤3.由r（B）>1知r（A）≤1.于是由A的表达式得r（A）=1，从而有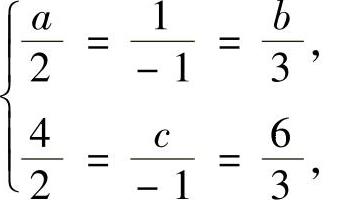即a=-2，b=-3，c=-2.

（ⅱ）将（ⅰ）中算得的a，b，c代入A得

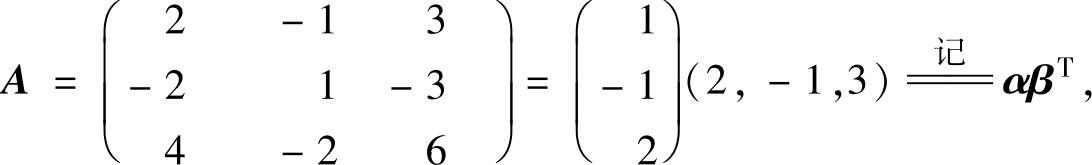
则

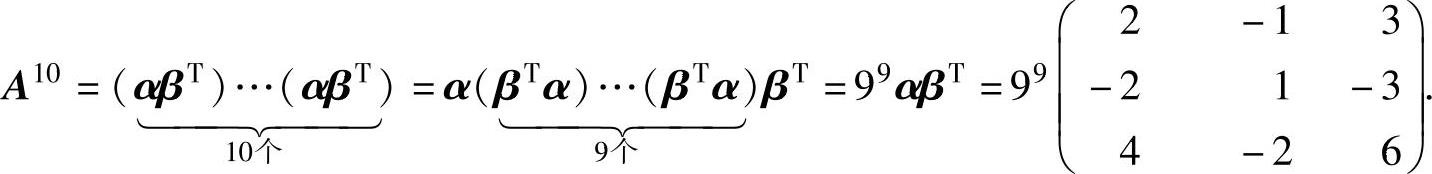
（13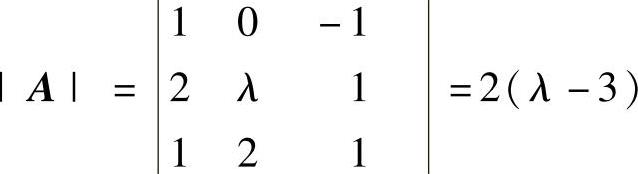），若λ≠3，则A可逆，从而r（AB）=r（B）=

2.与题设矛盾.从而λ=3.

（14）记A的三阶子行列式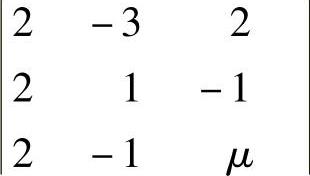为D₃，令D₃=0得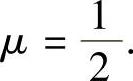所以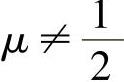

时r（A）=3.

当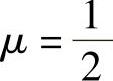时，对A施行初等行变换.(https://www.daowen.com)

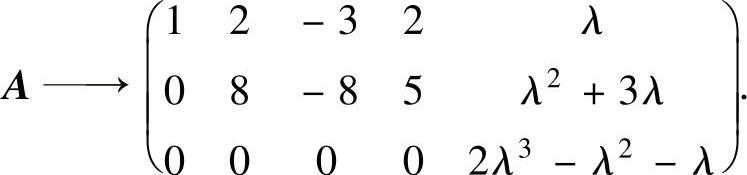
由此可知，当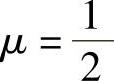，且2λ³-λ²-λ≠0时，即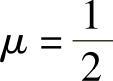，且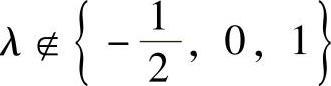时，r（A）=3；

当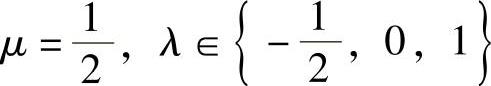时，r（A）=2.

（15）由于B=E_n-2A-A²=A³-A²-2A=A（A+E_n）（A-2E_n），

其中，由A³=E_n，即A·A²=E_n知A可逆，且A^-1=A²；由A³=E_n，即A³+E_n=2E_n或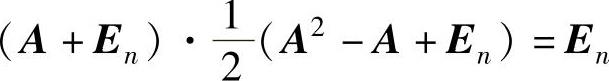知A+E_n可逆，且

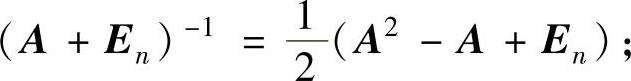
由A³=E_n，即A³-（2E_n）3=-7E_n或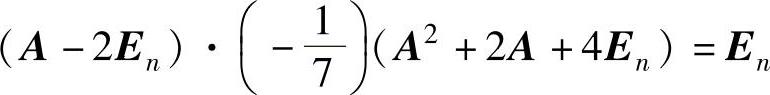知A-

2E_n可逆，且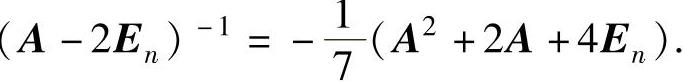

由此可知B可逆，且

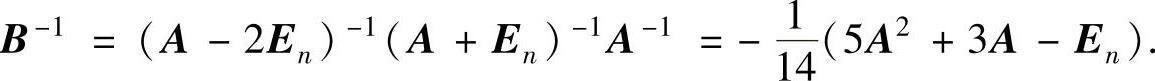
（16）由

知r（A）=2，所有的极大线性无关组为α₁，α₃与α₂，α₃.

（17）记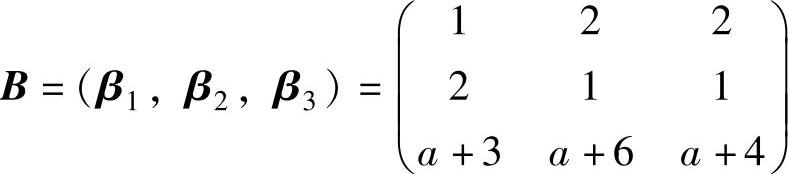，则|B|=6≠0.所以β₁，β₂，β3

线性无关，从而（Ⅰ）可由（Ⅱ）线性表示.记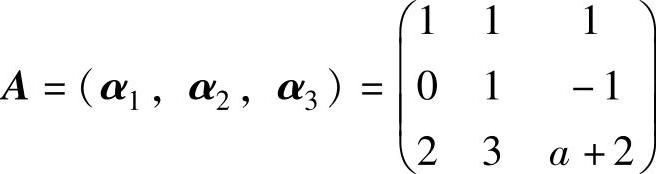，则|A|=a+1.由此可知，当a≠-1时，α₁，

α₂，α₃线性无关，此时（Ⅱ）可由（Ⅰ）线性表示，即（Ⅰ）与（Ⅱ）等价（当a=-1时由r（α₁，α₂，α₃）<r（β₁，β₂，β₃）知，（Ⅰ）与（Ⅱ）不等价）.

（18）正交化：

β₁=α₁=（1，1，0，0），

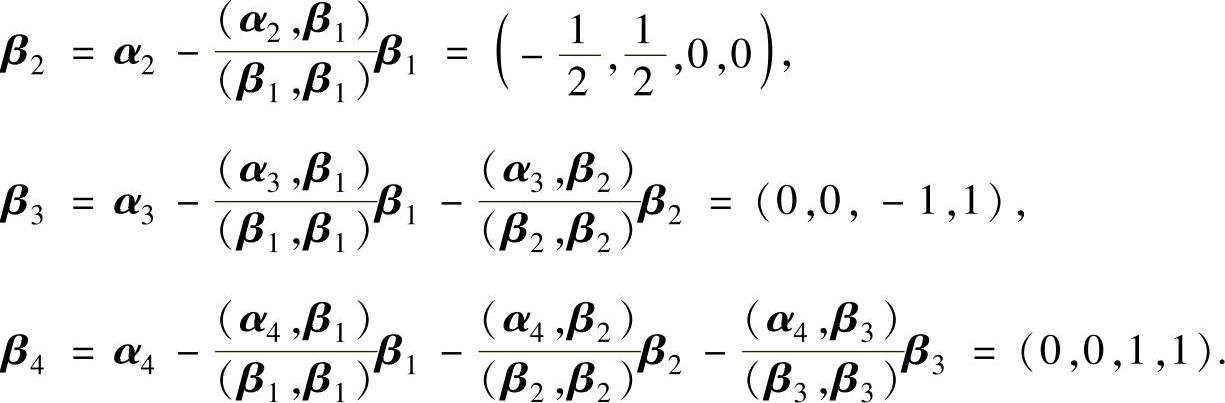
单位化：

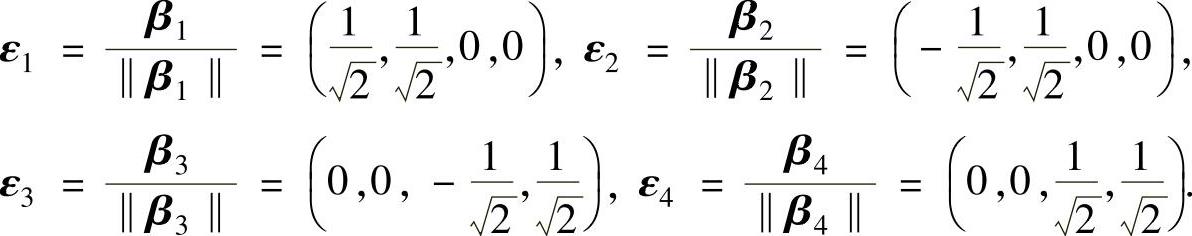
α₁，α₂，α₃，α₄的正交单位向量组为ε₁，ε₂，ε₃，ε_4.

（19）假设存在数k₁，k₂，…，k_s使得k₁α₁+k₂α₂+…+k_s-1α_s-1+k_sα_s=0.此外由题设知

（A-E）α₁=0，

（A-E）α₂=α₁，即（A-E）2α₂=0，

（A-E）α₃=α₂，即（A-E）2α₃=α₁，（A-E）3α₃=0，

︙

（A-E）α_s-1=α_s-2，即（A-E）s-2α_s-1=α₁，（A-E）s-1α_s-1=0，

（A-E）α_s=α_s-1，（A-E）s-1α_s=α₁，

所以

k₁（A-E）s-1α₁+k₂（A-E）s-1α₂+…+k_s-1（A-E）s-1α_s-1+k_s（A-E）s-1α_s=0，

即 k_sα₁=0.由此得k_s=0.从而有

k₁α₁+k₂α₂+…+k_s-1α_s-1=0.

于是同样可证 k_s-1=k_s-2=…=k₁=0.因此α₁，α₂，…，α_s线性无关.

（20）由r（B）≥r（AB）=m，r（B）≤n≤m知r（B）=m=B的列数，所以B的列向量组线性无关.

（21）由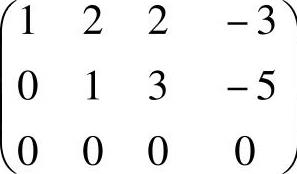知，β₁=-4α₁+3α₂，β₂=7α₁-5α₂.所以，对于不全为零的k₁，k₂，非零

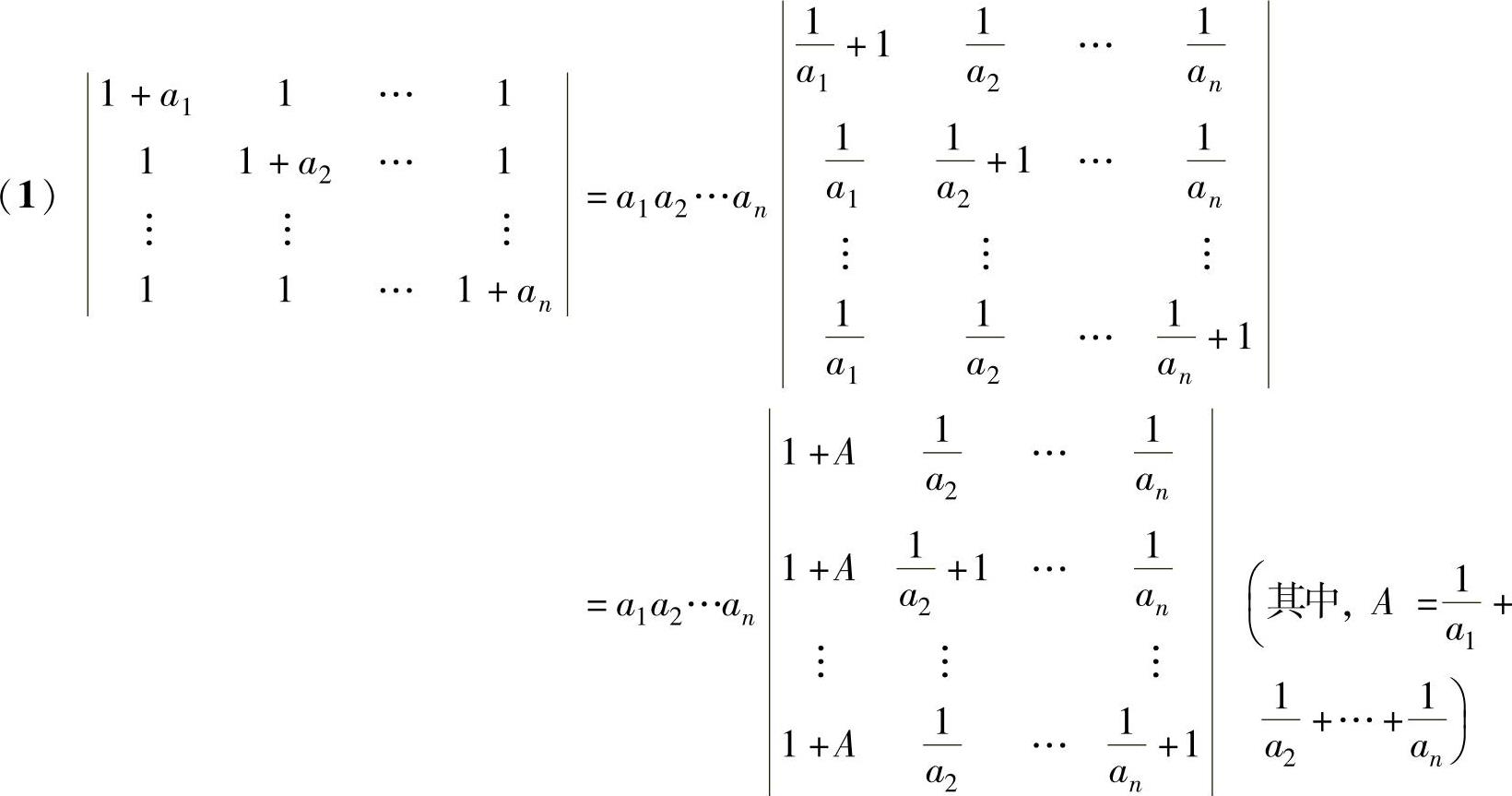
向量k₁β₁+k₂β₂=（-4k₁+7k₂）α₁+（3k₁-5k₂）α₂可以由β₁，β₂线性表示，也可由α₁，α₂线性表示.因此所求的非零向量为