实对称矩阵正交相似对角化

八 、实对称矩阵正交相似对角化

【主要内容】

1.实对称矩阵的定义与性质

设A是对称矩阵（即A^T=A），且每个元素都是实数，则称A为实对称矩阵.

设A是n阶实对称矩阵，则有以下性质：

（1）A的n个特征值都为实数.

（2）A的对应不同特征值的特征向量不仅线性无关，而且两两正交.

（3）A不仅可以相似对角化，而且还可以正交相似对角化，即可以找到正交矩阵Q，使得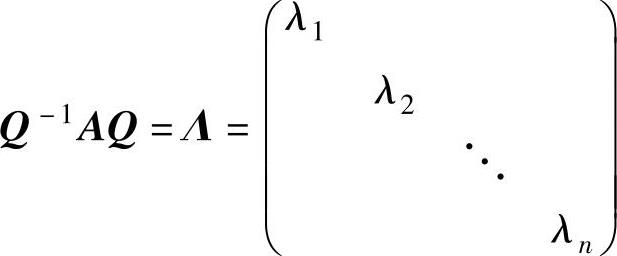（其中λ₁，λ₂，…，λ_n是A的n个特征值）.

（4）A不仅可以合同对角化，即可以找到可逆矩阵P，使得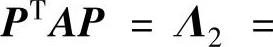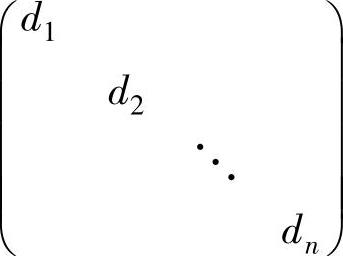，而且可以正交合同对角化，即可以找到正交矩阵Q，使得Q^-1AQ=Λ.

2.实对称矩阵特征向量的计算方法

实对称矩阵的特征向量可以按通常方法计算，但利用“实对称矩阵对应不同特征值的特征向量两两正交”这一性质，有时可较快地算出所有特征向量，现举例说明.

设三阶矩阵A的特征值为λ=1，2（二重），α=（1，-2，1）^T是对应特征值λ=1的特征向量，则对应特征值λ=2的特征向量x=（x₁，x₂，x₃）^T与α正交，从而有

（α，x）=0，即x₁-2x₂+x₃=0.该方程的基础解系为（2，1，0）^T，（-1，0，1）^T.所以对应特征值λ=2的所有特征向量为c₁（2，1，0）T+c₂（-1，0，1）^T（其中c₁，c₂是任意不全为零的常数）.

3.实对称矩阵正交相似对角化或正交合同对角化时，正交矩阵的计算方法

设A是n阶实对称矩阵，将它正交相似对角化或正交合同对角化时，满足Q^-1AQ=

Q^TAQ=Λ（对角矩阵）的正交矩阵Q可按以下步骤计算：

（1）计算A的所有特征值λ₁，λ₂，…，λ_n及它们对应的特征向量α₁，α₂，…，α_n；

（2）将α₁，α₂，…，α_n正交单位化得ε₁，ε₂，…，ε_n；

（3）写出Q=（ε₁，ε₂，…，ε_n），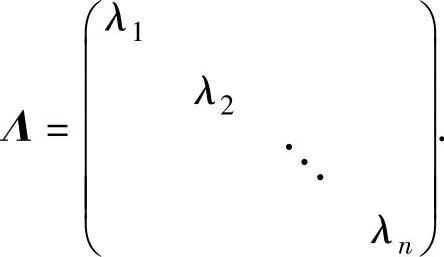

【典型例题】

例6.8.1 （单项选择题）设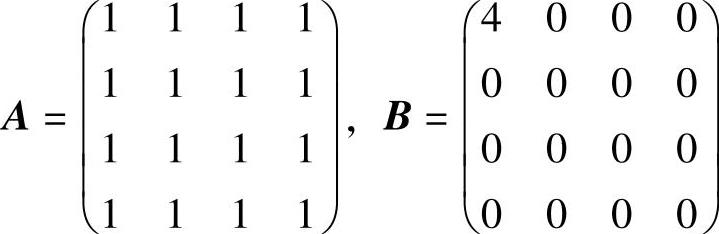，则A与B（ ）.

A.合同且相似 B.合同但不相似

C.相似但不合同 D.不合同也不相似

精解 从计算A的特征值入手.

由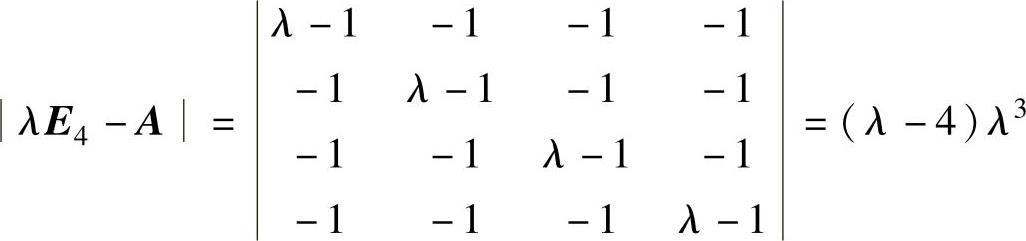知，A有特征值λ=4，0（三

重）.由于A是实对称矩阵，所以存在正交矩阵Q，使得

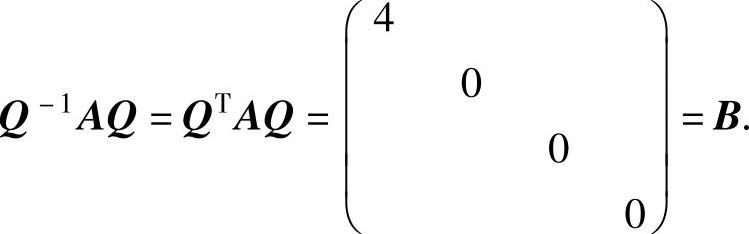
从而A与B相似且合同.

因此本题选A.

例6.8.2 设A是三阶实对称矩阵，其特征值为1，2，3，且α₁=（-1，-1，1）^T和α₂=（1，-2，-1）^T分别是A的对应特征值1，2的特征向量.试将A正交相似对角化，

即求三阶正交矩阵Q，使得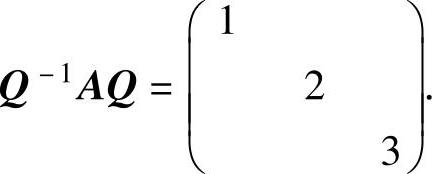

精解 设对应特征值3的特征向量为x=（x₁，x₂，x₃）^T，则由x与α₁，α₂都正交知x

满足方程组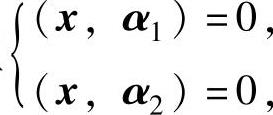即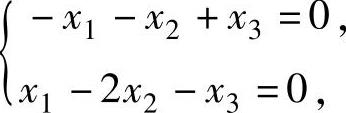它的基础解系为（1，0，1）T，从而是A的对

应特征值3的特征向量，记作α₃=（1，0，1）^T.

α₁，α₂，α₃两两正交，现将它们单位化得

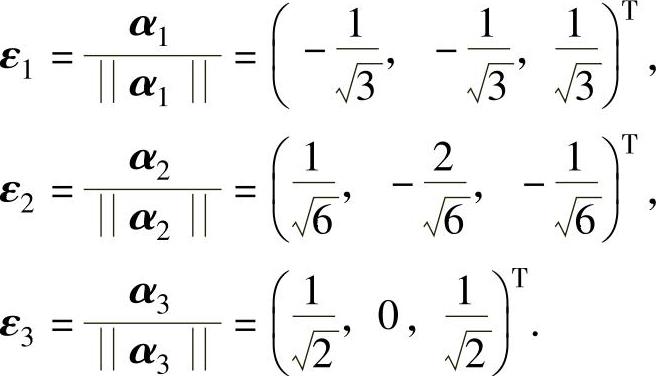
所以将A正交相似对角化的正交矩阵

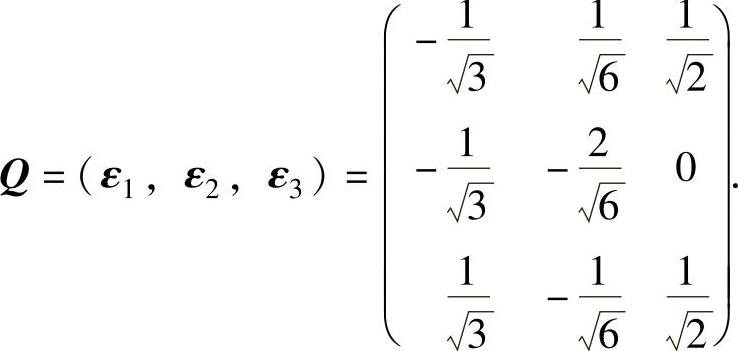
例6.8.3 设三阶实对称矩阵A的特征值为-1，1（二重），且ξ₁=（0，1，1）^T是对应特征值λ=-1的特征向量，求A.

精解 由A是实对称矩阵可知，存在正交矩阵Q，使得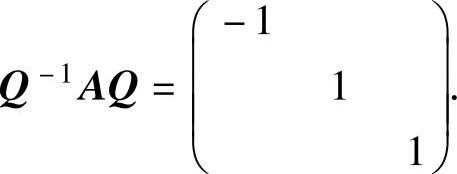因此

从计算Q入手，为此先计算A的对应特征值λ=1的特征向量.

设对应特征值λ=1的特征向量为x=（x₁，x₂，x₃）^T，则x满足

（x，ξ₁）=0，即x₂+x₃=0.该方程有基础解系（1，0，0）^T，（0，1，-1）^T，它们都是对应特征值λ=1的线性无关的特征向量，记ξ₂=（1，0，0）^T，ξ₃=（0，1，-1）^T.ξ₁，ξ₂，ξ₃是两两正交的向量组，现将它们单位化：

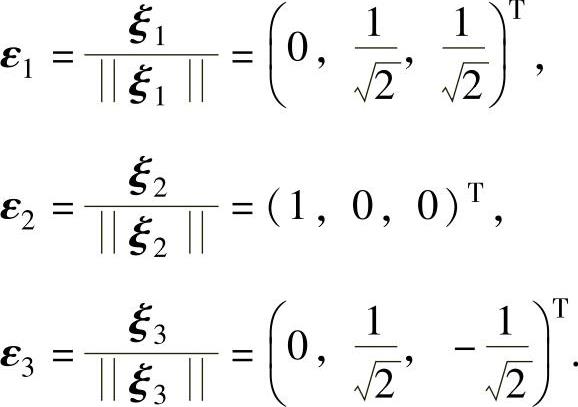
记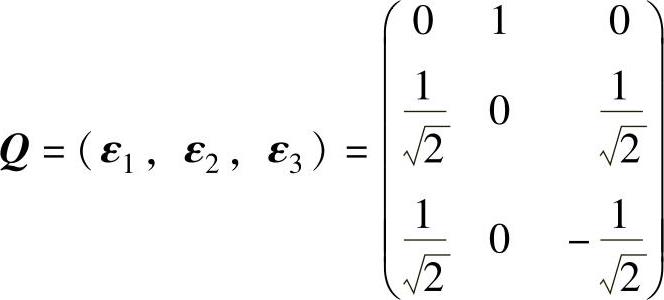（正交矩阵），则

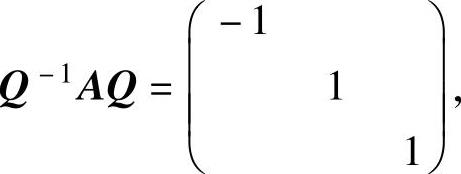
从而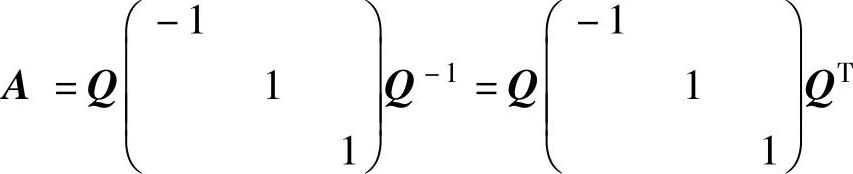

例6.8.4 设三阶实对称矩阵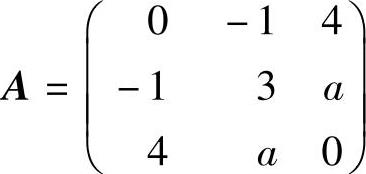，正交矩阵Q使A正交合同对角化，

其中，Q的第1列为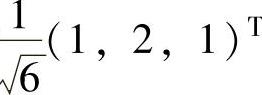.求常数a，Q及对角矩阵Λ.

精解 从“实对称矩阵正交合同对角化，即为正交相似对角化”入手.

由于Q使A正交合同对角化，即能使A正交相似对角化，因此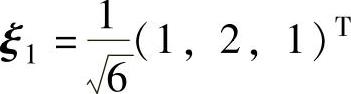是A的一个特征向量，记它对应的特征值为λ₁，则

（λ₁E₃-A）ξ₁=0.将A，ξ₁代入得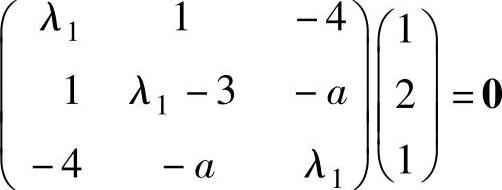，即

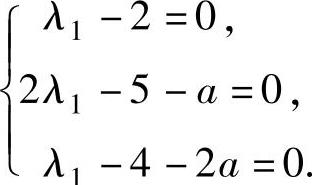
解此方程组得λ₁=2，a=-1.

将a=-1代入A得

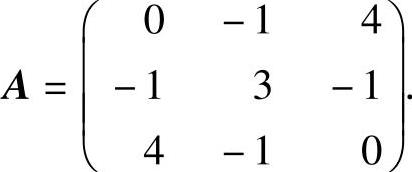
设A的另外两个特征值为λ₂，λ₃，则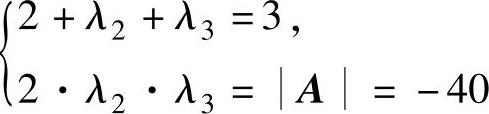{，即

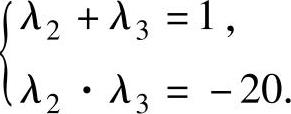
解此方程组得λ₂=5，λ₃=-4.

设A的对应于特征值λ₂=5的特征向量为x=（x₁，x₂，x₃）T，则x满足方程组

（5E₃-A）x=0，即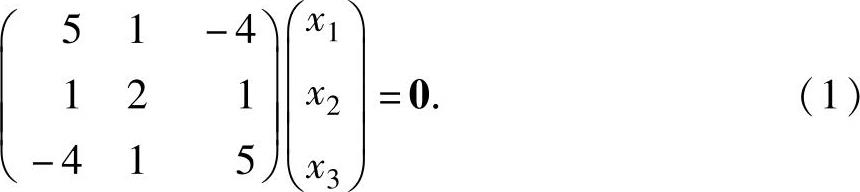

由于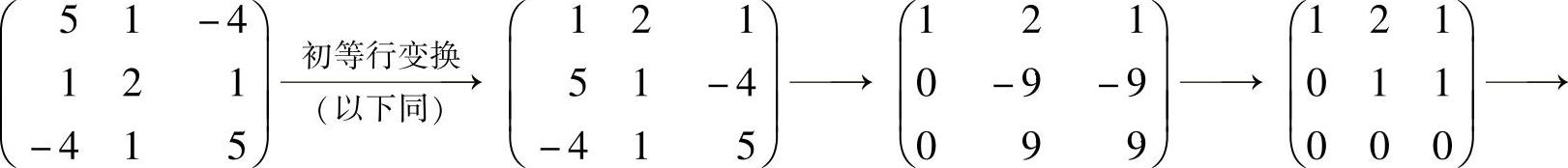

所以方程组（1）与方程组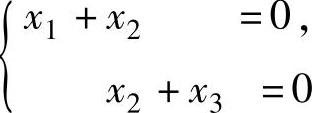同解，从而方程组（1）有基础解系（1，-1，

1）^T，它即为A的对应于特征值λ₂=5的特征向量，记为ξ₂=（1，-1，1）^T.

设A的对应于特征值λ₃=-4的特征向量为y=（y₁，y₂，y₃）^T，则由它分别与ξ₁，ξ₂正交得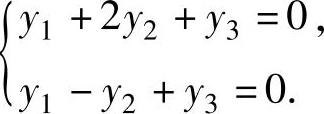即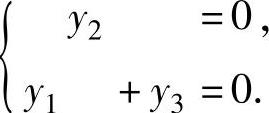

该方程组有基础解系（1，0，-1）^T，它即为A的对应于特征值λ₃=-4的特征向量，记为ξ₃=（1，0，-1）^T.

ξ₁，ξ₂，ξ₃两两正交，现在将它们单位化得

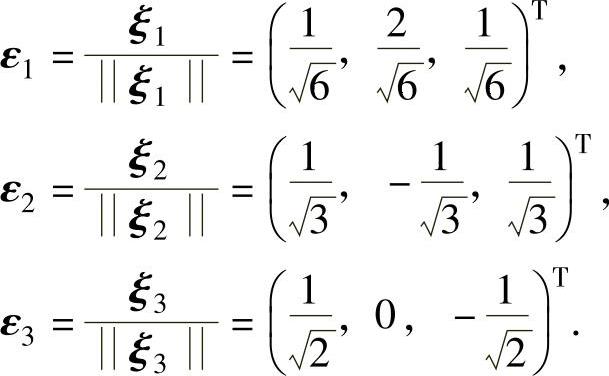
因此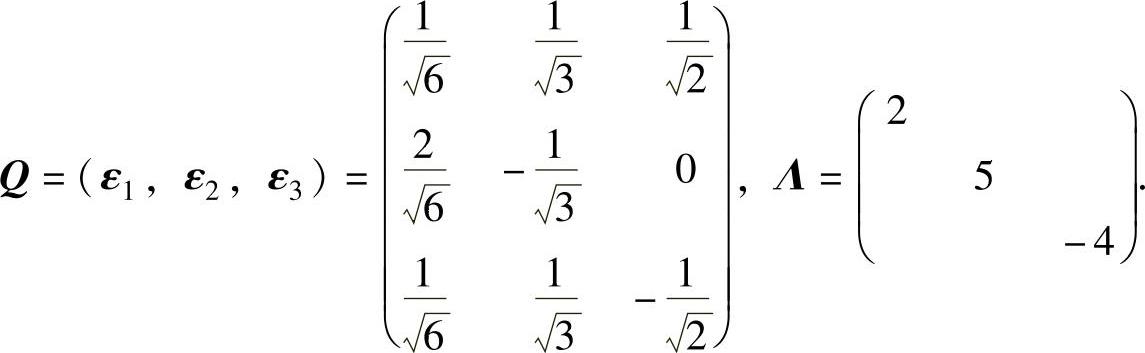

例6.8.5 设A，B都为n阶矩阵.

（1）如果A，B相似，证明：A，B的特征多项式相等；

（2）当A，B都为实对称矩阵时，证明：（1）的逆命题也成立.

精解 （1）用特征多项式定义证明.

由于A～B，所以存在n阶可逆矩阵P，使得P^-1AP=B，于是

A的特征多项式=λE_n-A=P^-1（λE_n-A）P=λE_n-P^-1AP

=λE_n-B=B的特征多项式.

（2）设n阶矩阵A，B的特征多项式相等，则A，B的特征值相同，记它们的特征值为λ₁，λ₂，…，λ_n，

由于A，B都是实对称矩阵，所以存在可逆矩阵P₁和P₂，使得

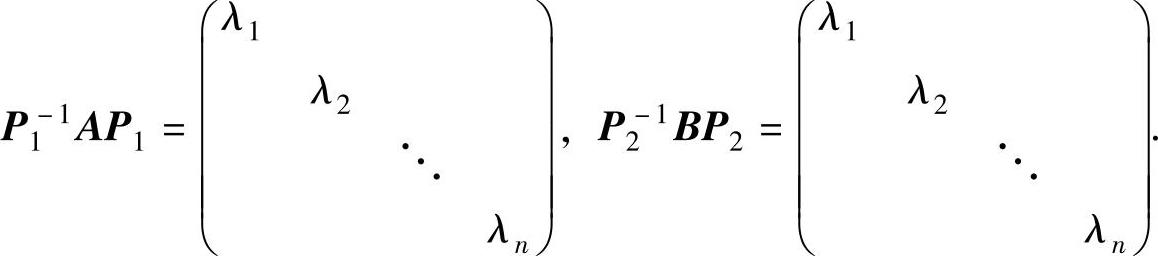
于是有P₁^-1AP₁=P₂^-1BP₂，即（P₂P₁^-1）A（P₁P₂^-1）=B，或（P₁P₂^-1）-1A（P₁P₂^-1）=B.由于P₁P₂^-1是可逆矩阵，所以A～B.