二重积分大小的比较与估计

十 、二重积分大小的比较与估计

【主要内容】

1.二重积分的比较

（1）相同积分区域情形

设f（x，y），g（x，y）都是连续函数.如果f（x，y）≤g（x，y）（（x，y）∈D），则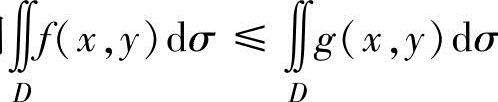σ，

如果f（x，y）≤g（x，y）（（x，y）∈D），但至少存在一点（x₀，y₀）∈D，使得

f（x₀，y₀）<g（x₀，y₀），则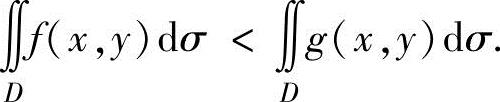

（2）不同积分区域情形

设f（x，y），g（x，y）都是连续函数，如果存在常数k，使得

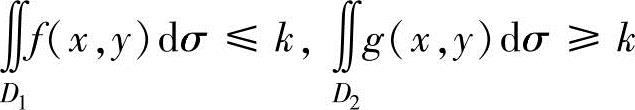
则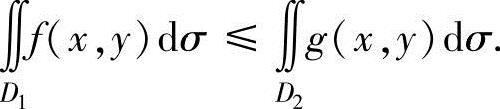设f（x，y），g（x，y）都是连续函数，如果存在常数k，使得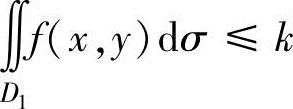（或<k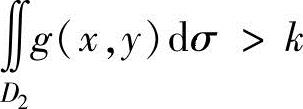），（或≥k），

则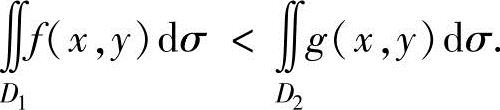

2.二重积分值的估计

当二重积分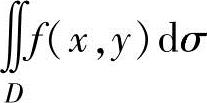（其中，f（x，y）是连续函数）不易计算时，往往需对它的值进行

估计，其方法有以下两种：

（1）如果f（x，y）在D上的最小值为m，最大值为M，则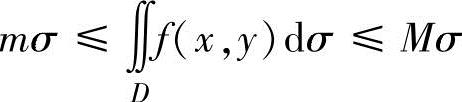（σ是D的面积）.

当f（x，y）在D上的最值不易计算时，可对f（x，y）作适当缩小或放大，得到

g（x，y）≤f（x，y）≤h（x，y）（（x，y）∈D），

并且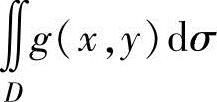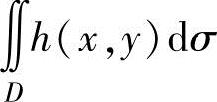，比较容易计算，记它们的值分别为A，B，则

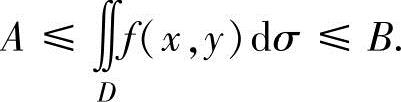
（2）将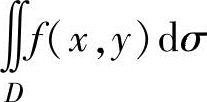转化成定积分，然后估计这个定积分，得到二重积分的估计值.

【典型例题】

例3.10.1 （单项选择题）如图3.10.1所示，正方形{（x，y）|x|≤1，|y|≤1}被其对角线划分为四个区域D_k（k=1，2，3，4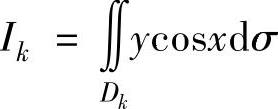），，则maxI_k=（）.

1≤k≤4

A.I₁ B.I₂ C.I₃ D.I₄

精解 利用积分区域的对称性，确定I₁，I₂，I₃，I₄与数零之间的关系，从而得到正确选项.

由于在D₁上ycosx≥0（且仅在点（0，0）处取等号），所以

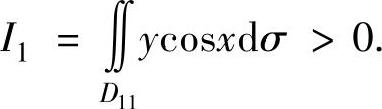
D₂和D₄都关于x轴对称，且在对称点处ycosx的值互为相反数，所以

I₂=I₄=0.

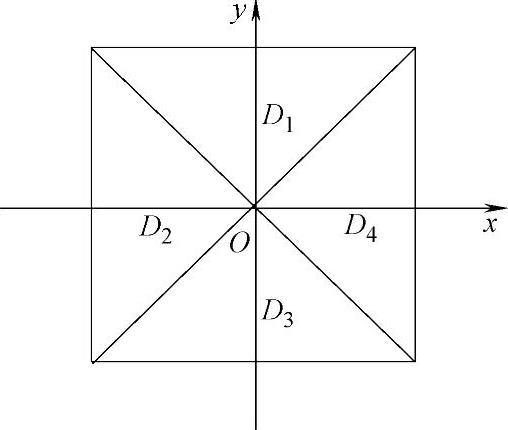
图 3.10.1

由于在D₃上ycosx≤0（且仅在点（0，0）处取等号），所以

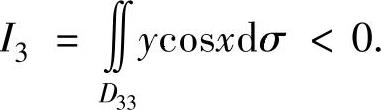
因此本题选A.

例3.10.2 （单项选择题）设平面区域D由直线x=0，y=0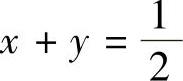，，x+y=1围

成，，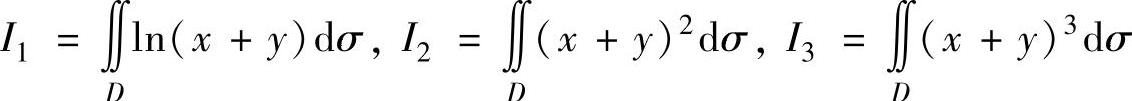

则I₁，I₂，I3的大小顺序是（）.(https://www.daowen.com)

A.I₁<I₂<I₃B.I₁<I₃<I₂C.I₃<I₁<I₂D.I₃<I₂<I₁

精解 由于I₁，I₂，I₃的积分区域同为D，所以只要比较被积函数的大小即可.在D上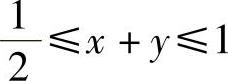，，所以有

ln（x+y）≤0≤（x+y）3≤（x+y）2，（1）并且ln（x+y），（x+y）2，（x+y）3都是D上的连续函数，且在D上至少存在一点使式（1）中的等号都不成立.所以有

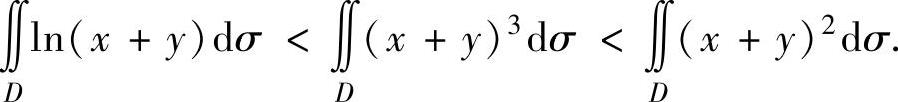
因此本题选B.

例3.10.3 估计二重积分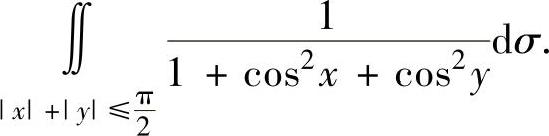

精解 由于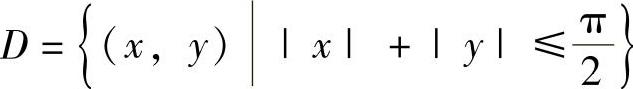既关于x轴对称，又关于y轴对称，且被

积函数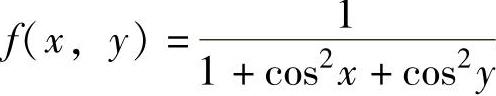在对称点处的值彼此相等，所以

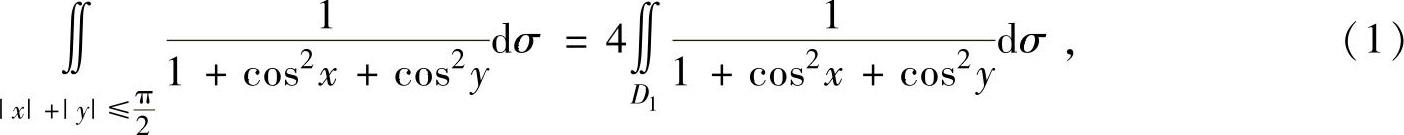
其中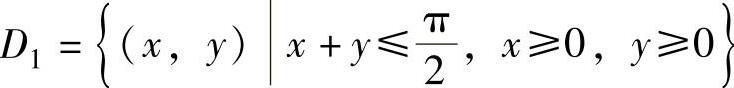，是D在第一象限的部分.

下面计算f（x，y）在D₁上的最小值m与最大值M.

由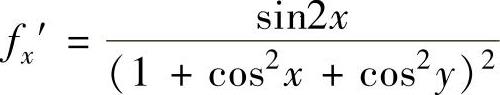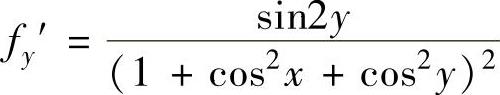，知f（x，y）在D₁的内部无极值

点.

D₁有边界C₁：，，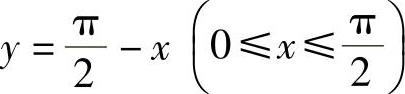

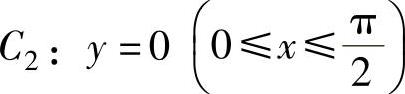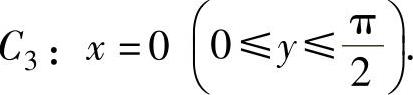
在C₁上；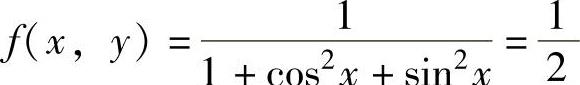

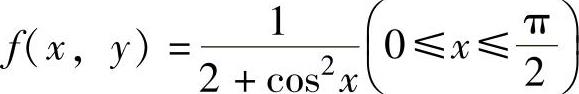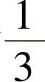在C₂上的最小值为，最大值为；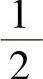

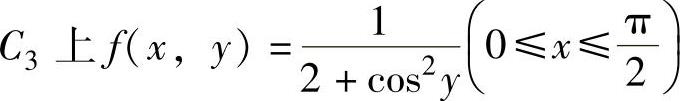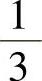同理，在的最小值为，最大值为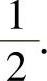

因此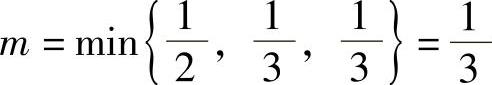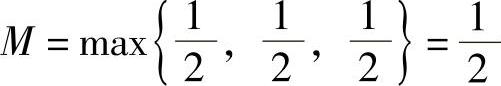，，于是由D₁的面积为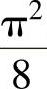得

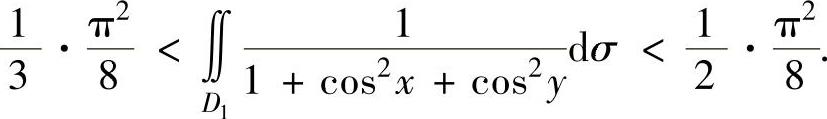
将它代入式（1）得，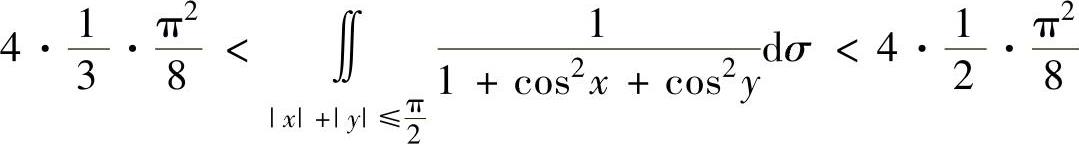

即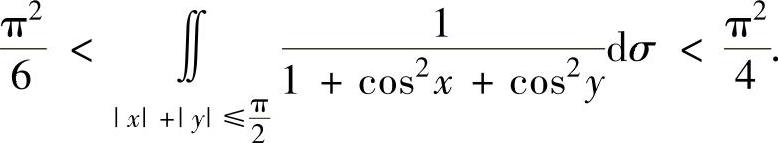

例3.10.4 估计二重积分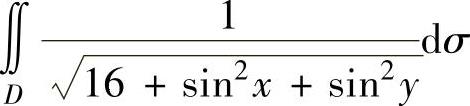的取值范围，其中，D={（x，y）|x²+y²≤1}.

精解 被积函数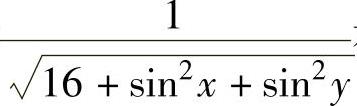在D上的最值不易计算，因此考虑对它作适当缩小

或放大，显然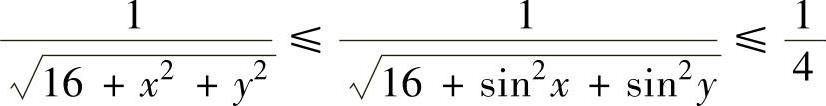（其中，（x，y）∈D，并且仅在点（0，0）处取等号），

于是有

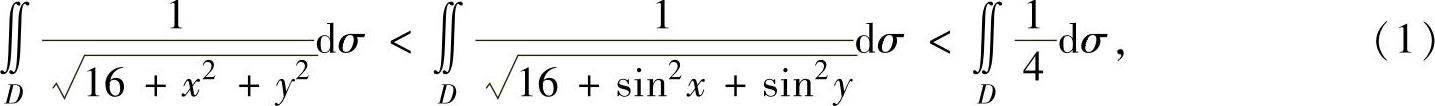
其中

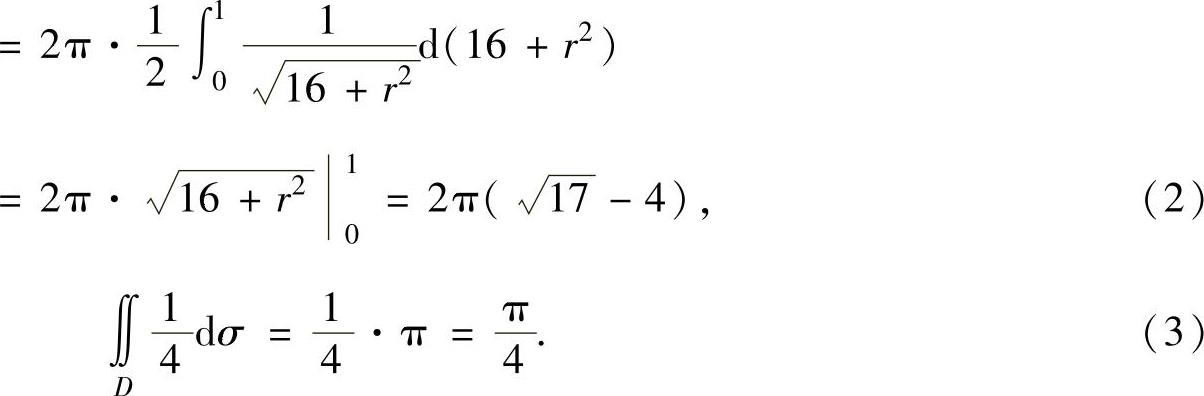
将式（2）和式（3）代入式（1）得

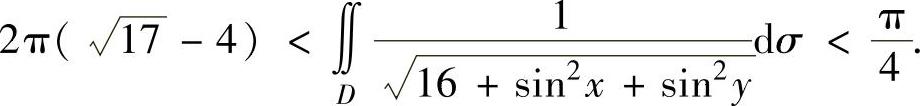
例3.10.5 估计二重积分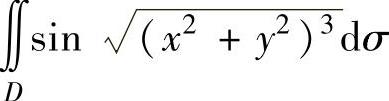，其中，D={（x，y）|x²+y²≤1}.

精解 用极坐标容易将题中所给的二重积分转化成定积分，然后通过估计定积分得到二重积分的估计值.

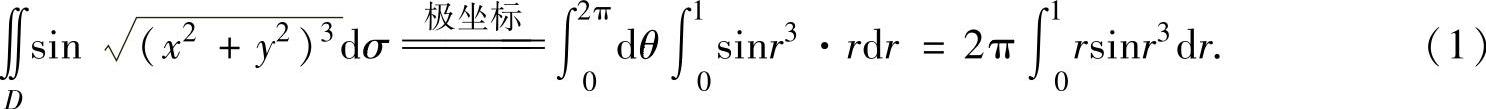
由于当u≥0时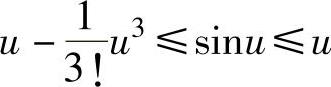，（等号仅在u=0处成立），所以有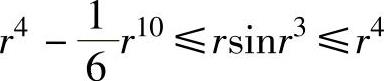（等号仅在r=0处成立）.

因此有，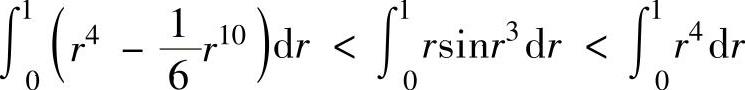

即

将式（2）代入式（1）得