二元复合函数偏导数及二阶偏导数的计算

三 、二元复合函数偏导数及二阶偏导数的计算

【主要内容】

设二元函数u=u（x，y），v=v（x，y）在点（x，y）处偏导数存在，函数z=f（u，v）在对应点（u，v）处可微，则复合函数z=f（u（x，y），v（x，y））在点（x，y）处的偏导数存在，且

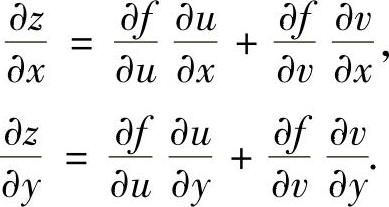
二元以上复合函数的偏导数也有类似的计算公式.

注 在计算二元或二元以上复合函数的偏导数时，应先画出复合函数的关系图，然后按此图用复合函数求偏导数公式计算.例如，二元复合函数z=f（u（x，y），v（x））的关系图为

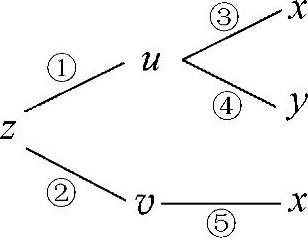
由关系图可见，z与x之间有两条通路：①—③，②—⑤，所以

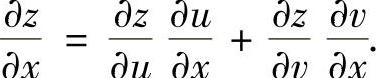
复合函数f的二阶偏导数可以通过对已求得的一阶偏导数再求偏导数得到，但当复合函数f是抽象函数时，对一阶偏导数再求偏导数时总是认为一阶偏导数有与复合函数f本身相同的复合函数关系图.

【典型例题】

例3.3.1 设z=f（e^xsiny，x²+y²），其中，二元函数f（u，v）具有二阶连续偏导数，求，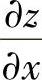

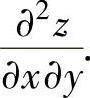
精解 由于u=e^xsiny，v=x²+y²，所以z与x，y的复合函数关系图如图3.3.1所示，由图可知，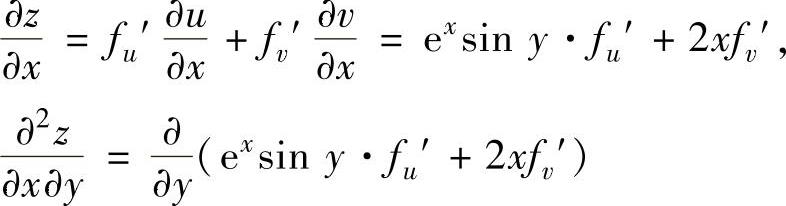

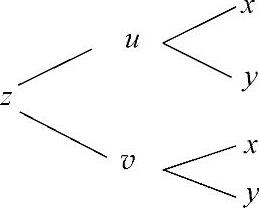
图 3.3.1

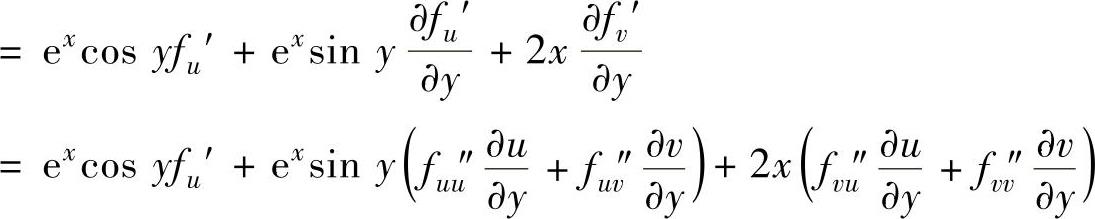（可以认为f_u′，f_v′都有与f同样的复合函数关系图）=e^xcosyf_u′+e^xsiny（e^xcosyf_uu″+2yf_uv″）+2x（e^xcosyf_uv″+2yf_vv″）=e^xcosyf_u′+e^2xsinycosyf_uu″+2e^x（ysiny+xcosy）f_uv″+4xyf_vv″.

例3.3.2 设二元函数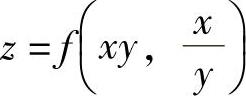，其中，f（u，v）有二阶连续偏导数，求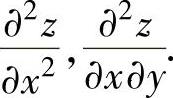

精解 先算出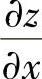，然后计算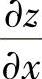的全微分，从而确定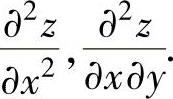

记u=xy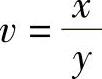，，则z与x，y的复合函数关系如图3.3.2所示.

由图可知，

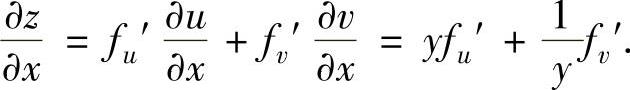
由此可得

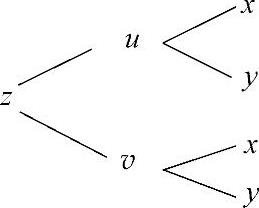
图 3.3.2

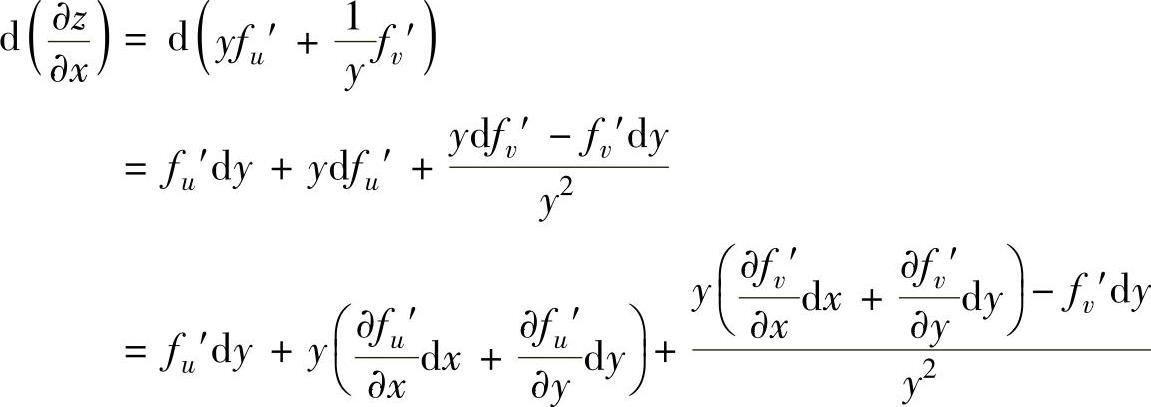
(https://www.daowen.com)

所以，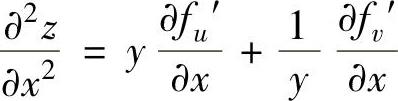

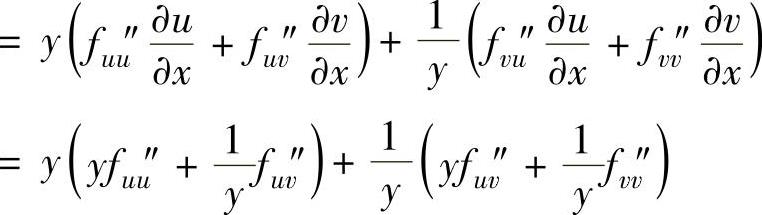
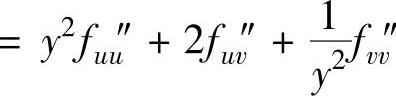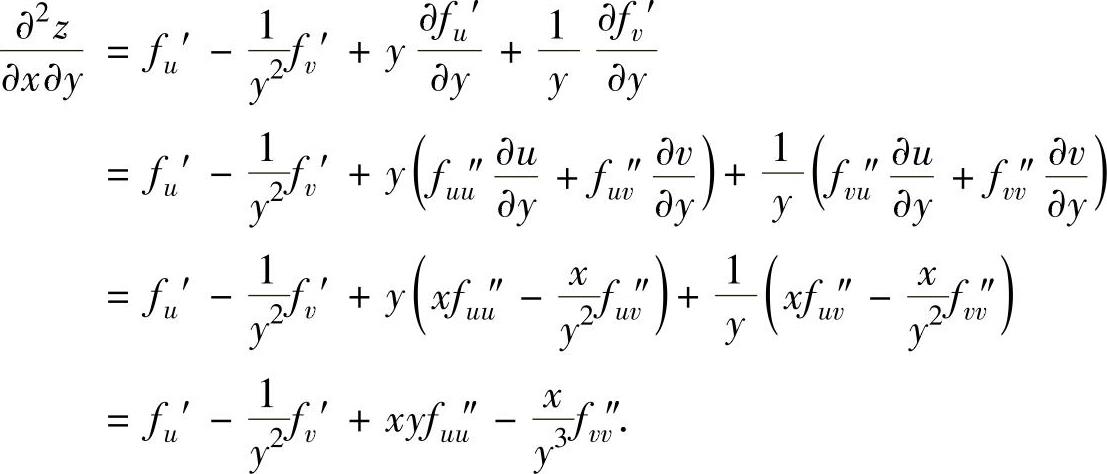
注 在同时计算二元复合函数z=f（u（x，y），v（x，y））的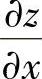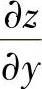，时，可利用全微分形

式不变性，从计算dz入手较为快捷，同样在同时计算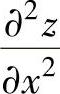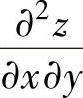，时，可从计算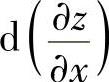入手.

例3.3.3 设f（u，v）具有二阶连续偏导数，且满足f_x″_x+f_y″_y=1，又g（x，y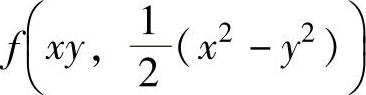）=，求g_x″_x+g_y″y.

精解 先算出g_x″_x，g_y″_y，然后利用f_x″_x+f_y″_y=1计算g_x″_x+g_y″y.

记u=xy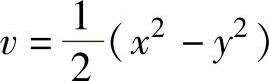，，则g（x，y）的复合函数关系如图3.3.3所示.

于是由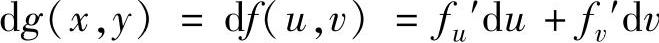

得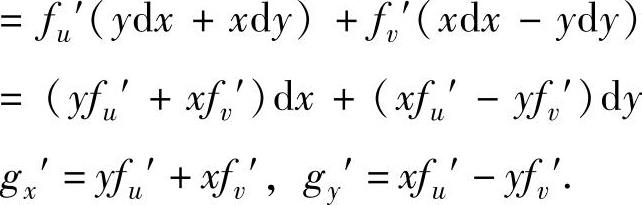

从而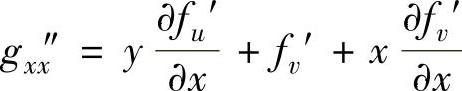

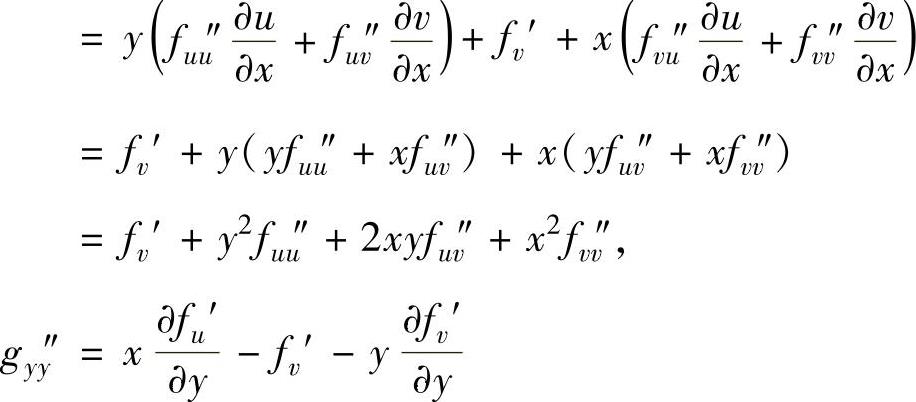
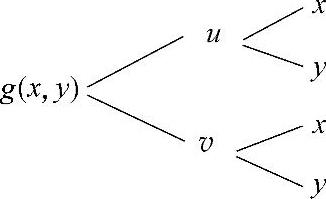
图 3.3.3

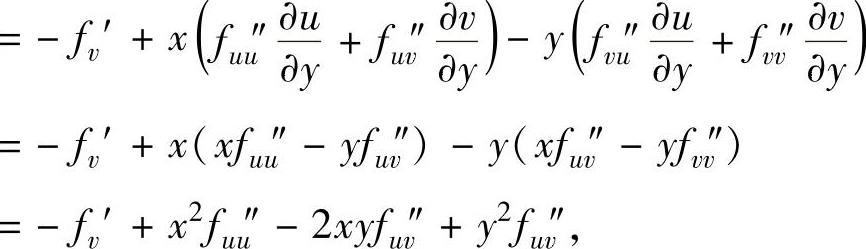
由此得到

g_x″_x+g_y″_y=（x²+y²）（f_u″_u+f_v″_v）=x²+y²

（利用题设f_x″_x+f_y″_y=1，即f_u″_u+f_v″_v=1）.

例3.3.4 设二元函数u=u（x，y）有连续的二阶偏导数，并满足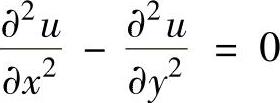，且u（x，2x）=x，u_x′（x，2x）=x².求u_x″_x（x，2x），u_x″_y（x，2x）.

精解 先计算du_x′（x，2x）得到一个关于u_x″_x（x，2x）与u_x″_y（x，2x）的关系式.再由u（x，2x）=x得到另一个关于u_x″_x（x，2x）与u_x″_y（x，2x）的关系式.

由于 du_x′（x，2x）=u_x″_x（x，2x）dx+u_x″_y（x，2x）·2dx

=[u_x″_x（x，2x）+2u_x″_y（x，2x）]dx，另一方面，由题设u_x′（x，2x）=x²得du_x′（x，2x）=2xdx，所以

u_x″_x（x，2x）+2u_x″_y（x，2x）=2x.（1）

对u（x，2x）=x两边求全微分得

u_x′（x，2x）dx+2u_y′（x，2x）dx=dx，即 u_x′（x，2x）+2u_y′（x，2x）=1.上式两边对x求偏导数得

u_x″_x（x，2x）+2u_x″_y（x，2x）+2u_y″_x（x，2x）+4u_y″_y（x，2x）=0，即5u_x″_x（x，2x）+4u_x″_y（x，2x）=0（2）

（由于u有二阶连续偏导数，所以u_x″_y=u_y″_x，此外由题设知u_y″_y=u_x″_x）.

将式（1）和式（2）联立得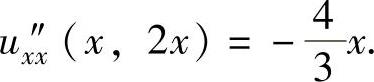从而由式（1）得