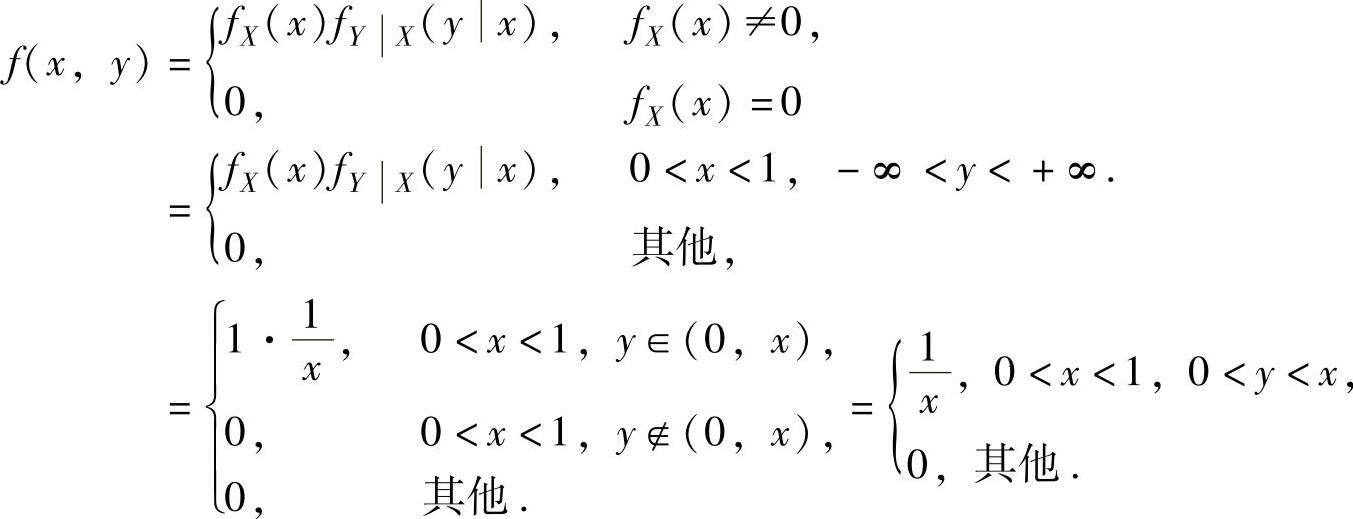二维连续型随机变量及其概率密度
【主要内容】
1.二维连续型随机变量及其概率密度的定义
设(X,Y)是二维随机变量,如果存在非负可积函数f(x,y)(-∞<x<+∞,-∞<y<+∞),使得xOy平面上的任意区域G,有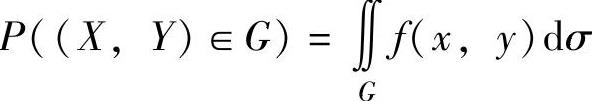 ,
,
则称(X,Y)是二维连续型随机变量,称f(x,y)为(X,Y)的概率密度,或X、Y的联合概率密度,其中f(x,y)有以下性质:
(1)f(x,y)非负可积;
(2)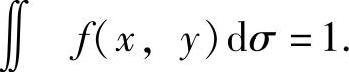
xOy平面
2.常用的二维连续型随机变量
(1)在区域G上服从均匀分布的二维随机变量设二维随机变量(X,Y)的概率密度为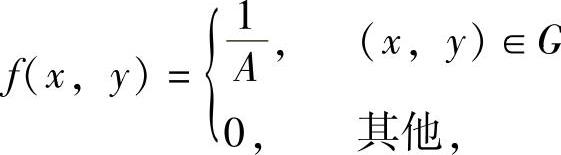 ,(其中,A是G的面积且A≠0),则称(X,Y)是在区域G上服从均匀分布的二维随机变量,简称(X,Y)在G上服从均匀分布.
,(其中,A是G的面积且A≠0),则称(X,Y)是在区域G上服从均匀分布的二维随机变量,简称(X,Y)在G上服从均匀分布.
(2)服从正态分布的二维随机变量
设二维随机变量的概率密度为
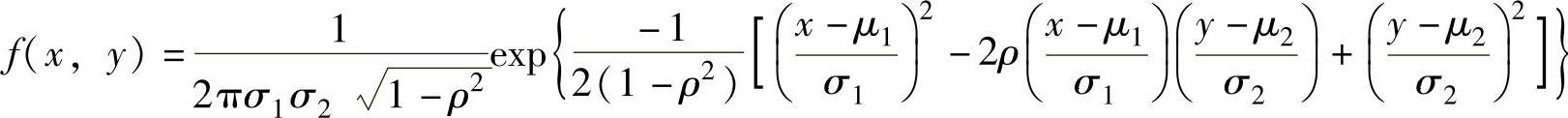
(-∞<x<+∞,-∞<y<+∞),则称(X,Y)是服从参数为μ1,μ2,σ21,σ22,ρ(其中μ1,μ2是实数,σ1,σ2为正数,ρ<1)的正态分布的二维随机变量,简称(X,Y)服从参数为μ1,μ2,σ21,σ22,ρ的正态分布,记为(X,Y)~N(μ1,μ2,σ21,σ22,ρ).
3.二维连续型随机变量的边缘概率密度
设(X,Y)是二维连续型随机变量,概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),则分别称X,Y的概率密度fX(x),fY(y)为(X,Y)关于X和关于Y的边缘概率密度,其中
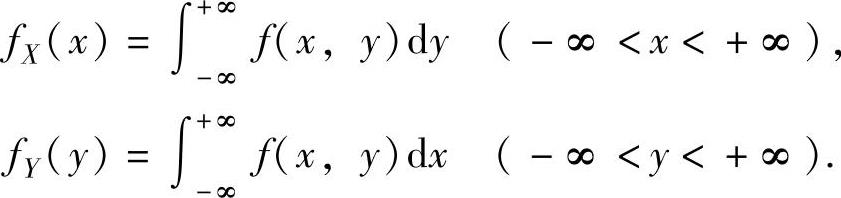
4.二维连续型随机变量的条件概率密度
设(X,Y)是连续型随机变量,它的概率密度、边缘概率密度分别为f(x,y),fX(x)与fY(y)(-∞<x<+∞,-∞<y<+∞),则
当y满足fY(y)>0时,称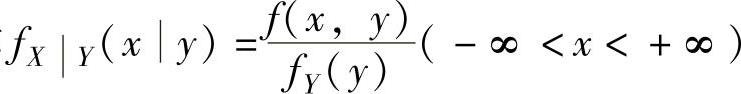 为在条件Y=y下X的
为在条件Y=y下X的
条件概率密度;
当x满足fX(x)>0时,称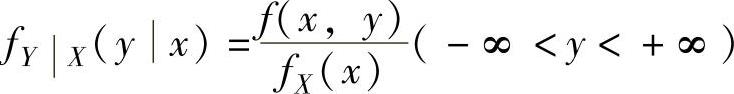 为在条件X=x下Y的
为在条件X=x下Y的
条件概率密度.
【典型例题】
例7.10.1 设二维随机变量(X,Y)的概率密度为
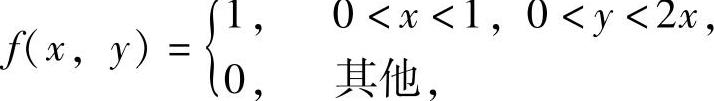
求(X,Y)的边缘概率密度fX(x)与fY(y).
精解 先画出f(x,y)的值在xOy平面上的分布图,然后按边缘概率密度计算公式计算fX(x)与fY(y).
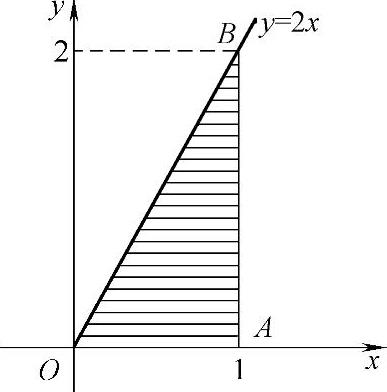
f(x,y)在如图7.10.1所示的带阴影的△OAB内取值为1,在xOy平面的其余部分都取值为零.
 (https://www.daowen.com)
(https://www.daowen.com)
图 7.10.1
由图可知,关于X的边缘概率密度为
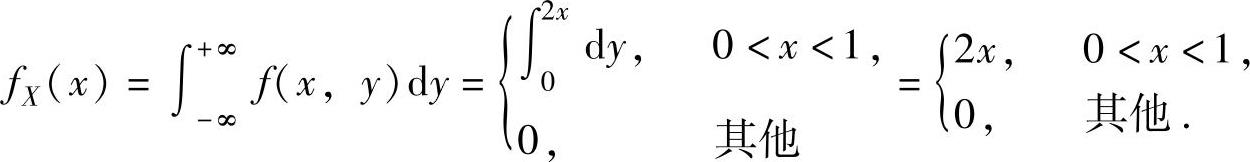
同样,由图可知,关于Y的边缘概率密度为
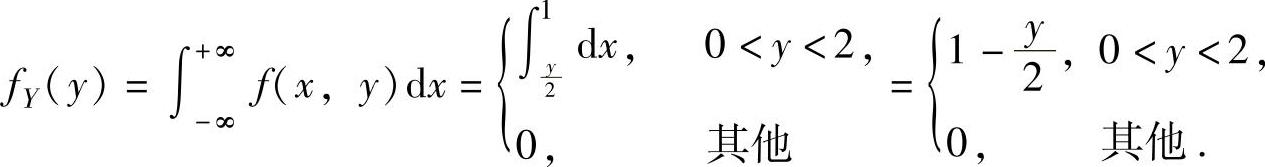
例7.10.2 设二维随机变量(X,Y)在如图7.10.2阴影部分所示的区域D={(x,y)y≤x<2-y,0≤y≤1}上服从均匀分布,求:
(1)(X,Y)的关于X和关于Y的边缘概率密度fX(x)和fY(y);
(2)概率P(2X+Y≤2).
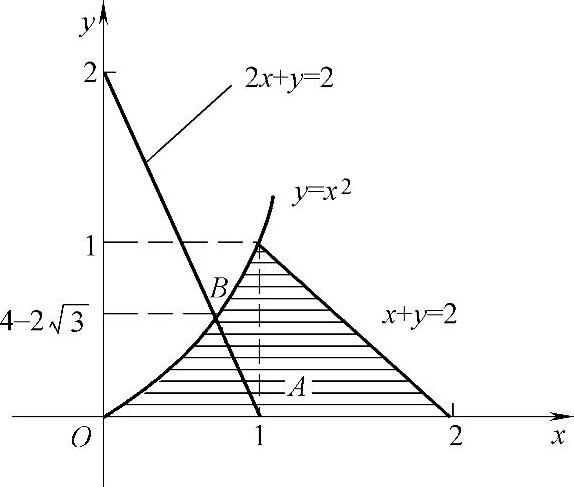
图 7.10.2
精解 (1)先写出(X,Y)的概率密度f(x,y)的表达式,然后根据边缘概率密度计算公式计算fX(x)与fY(y).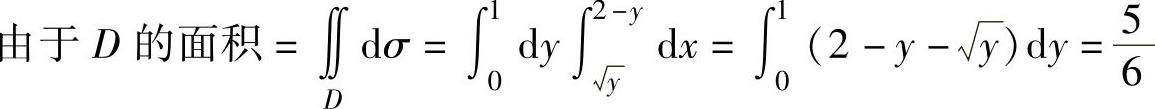 ,所以(X,Y)的概率密度
,所以(X,Y)的概率密度
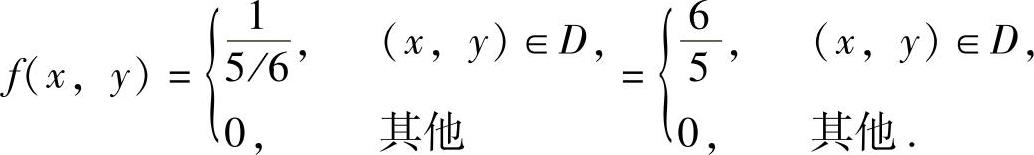
由此由边缘概率密度计算公式可得

(2)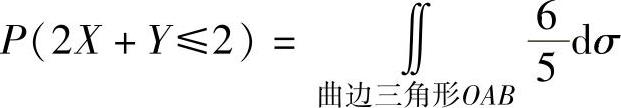
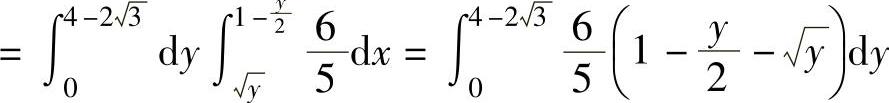
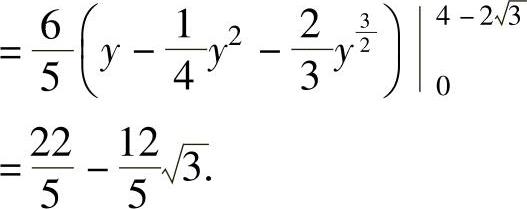
例7.10.3 设二维随机变量(X,Y)的概率密度为
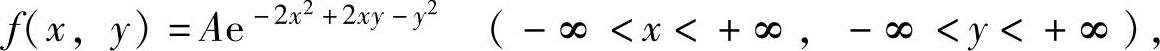
求常数A及条件概率密度fYX(yx).
精解 先算出关于X的边缘概率密度fX(x),然后利用概率密度的性质算出常数A并利用条件概率密度计算公式算出fYX(yx).
由于关于X的边缘概率密度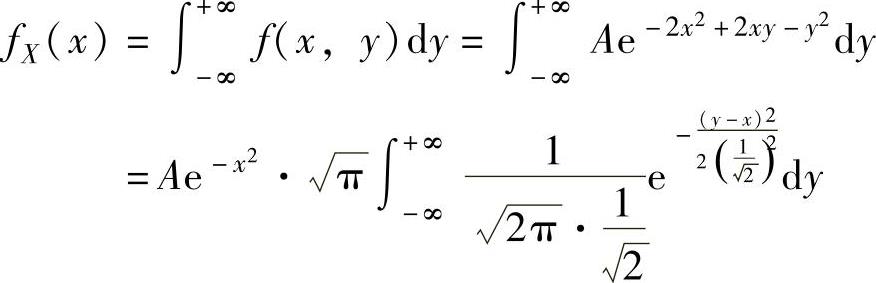
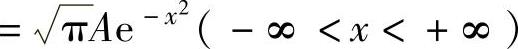 (这是由于
(这是由于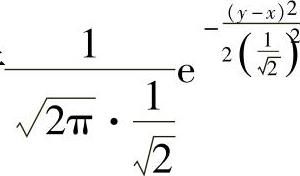 是服从
是服从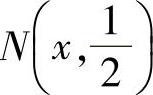 的随机变
的随机变
量的概率密度,所以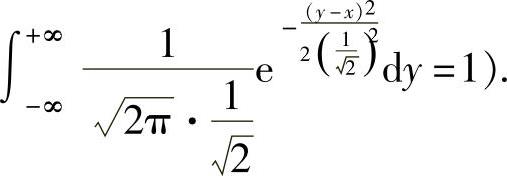
其中,由常数A满足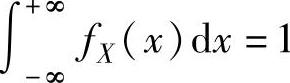 ,即
,即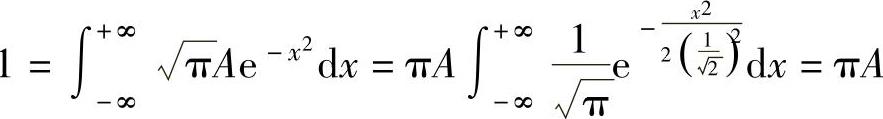 得
得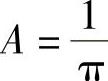 ,并且
,并且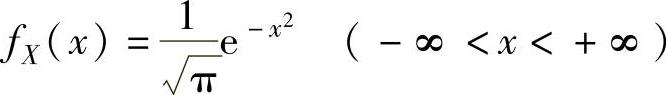 ,
,
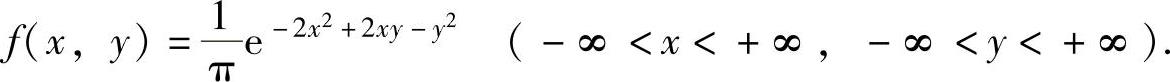
由于,fX(x)≠0(-∞<x<+∞),所以对任意x∈(-∞,+∞)有
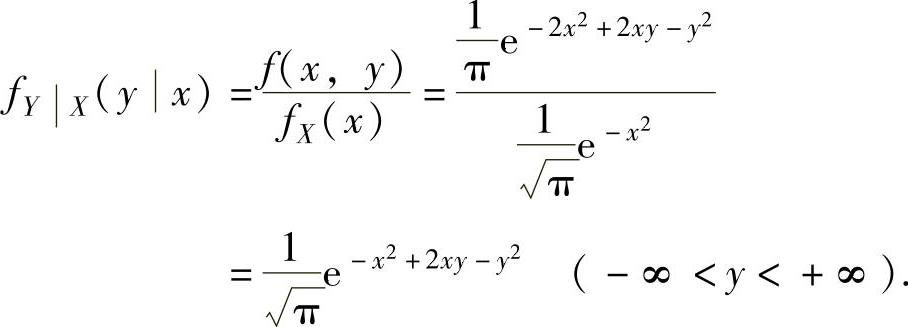
例7.10.4 设随机变量X在(0,1)内服从均匀分布,在X=x(0<x<1)的条件下,随机变量Y在(0,x)内服从均匀分布,求二维随机变量(X,Y)的概率密度f(x,y).精解 X的概率密度为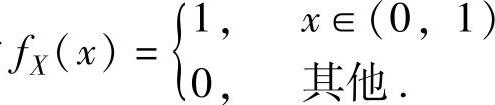 ,显然对任意x∈(0,1),fX(x)≠0.
,显然对任意x∈(0,1),fX(x)≠0.
此外,在X=x(0<x<1)的条件下随机变量在区间(0,x)内服从均匀分布,实际上给
出条件概率密度
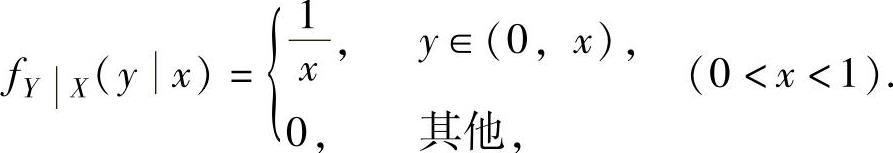
所以,