旋转体体积的计算

十三 、旋转体体积的计算

【主要内容】

1.旋转轴为x轴或与x轴平行的直线情形

（1）由曲线y=f（x）（f（x）是连续函数），直线x=a，x=b（a<b）及x轴围成的平面图形绕x轴旋转一周而成的旋转体体积

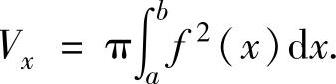
（2）由曲线y=f（x）（f（x）是连续函数），直线x=a，x=b（a<b）及x轴围成的平面图形绕直线y=k（对任意x∈[a，b]有0≤f（x）≤k）旋转一周而成的旋转体体积

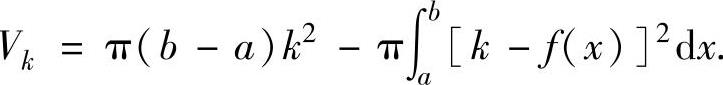
注 由曲线y=f（x）（f（x）是连续函数），直线x=a，x=b（0≤a<b或a<b≤0）及x轴围成的平面图形绕y轴旋转一周而成的旋转体体积

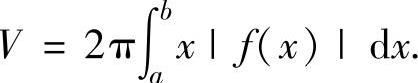
2.旋转轴为y轴或与y轴平行的直线情形

（1）由曲线x=g（y）（g（y）是连续函数），直线y=c，y=d（c<d）及y轴围成的平面图形绕y轴旋转一周而成的旋转体体积

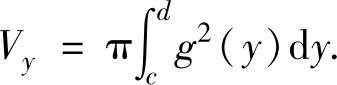
（2）由曲线x=g（y）（g（y）是连续函数），直线y=c，y=d（c<d）及y轴围成的平面图形绕直线x=m（对任意y∈[c，d]有0≤g（y）≤m）旋转一周而成的旋转体体积

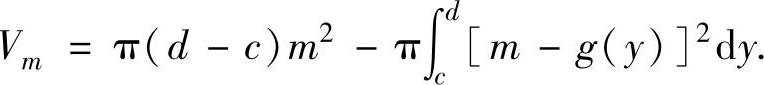
注 由曲线x=g（y）（g（y）是连续函数），直线y=c，y=d（0≤c<d或c<d≤0）及y轴围成的平面图形绕y轴旋转一周而成的旋转体体积

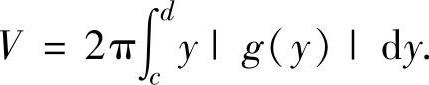
【典型例题】

例2.13.1 过点P（1，0）作抛物线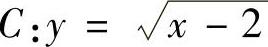的切线l，求由C，l及x轴围成的平面图

形D绕x轴旋转一周而成的旋转体体积V.

精解 先写出l的方程，然后画出D的图形并计算V.

设l与抛物线C的切点为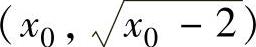，则x₀>2，且l的方程为

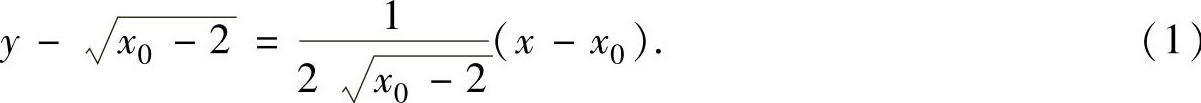
由于l过点P（1，0），故将其坐标值代入式（1）得

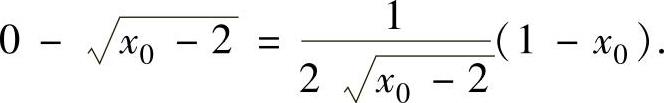
解此方程得x₀=3，从而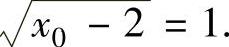将

它们代入式（1）得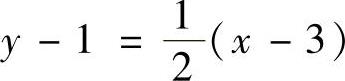，即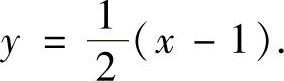

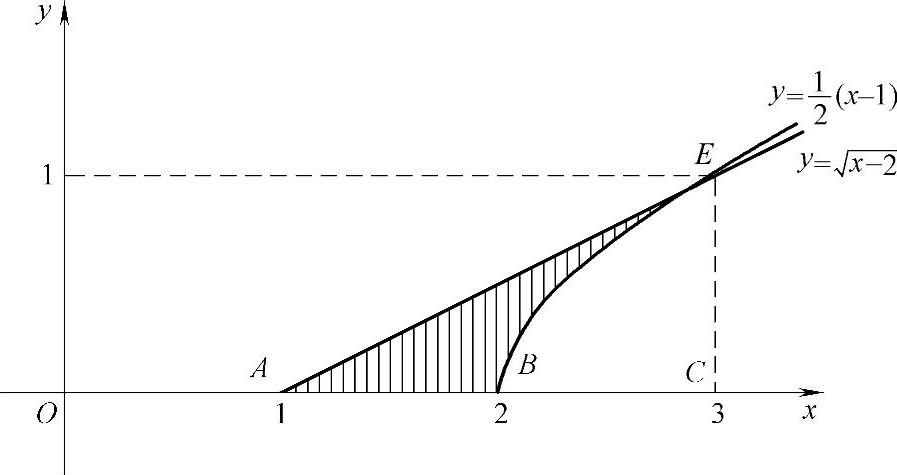
图 2.13.1(https://www.daowen.com)

由此可以画出D的图形如图2.13.1的阴影部分所示.

V=△ACE绕x轴旋转一周而成的旋转体体积-

曲边三角形BCE绕x轴旋转一

周而成的旋转体体积

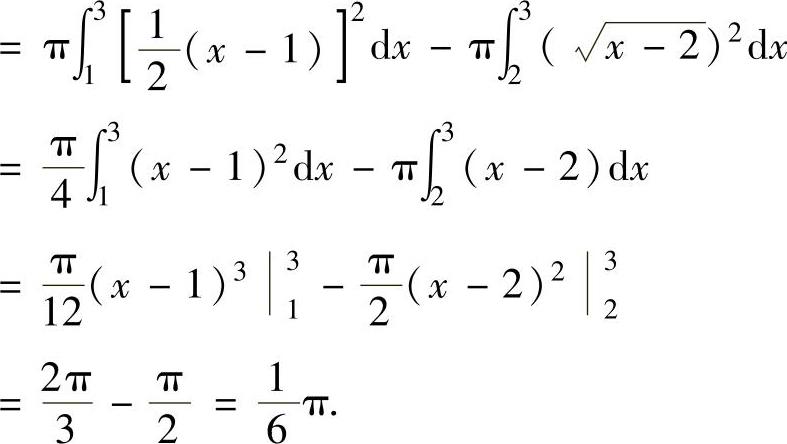
例2.13.2 设平面图形D={（x，y）x²+y²≤-2x，y≤x}.求D绕直线x=1旋转一周而成的旋转体体积V.

精解 D的图形如图2.13.2中的阴影部分所示.

V=△ABO绕直线x=1旋转一周而成的旋

转体体积-曲边三角形ABO绕直线

x=1旋转一周而成的旋转体体积

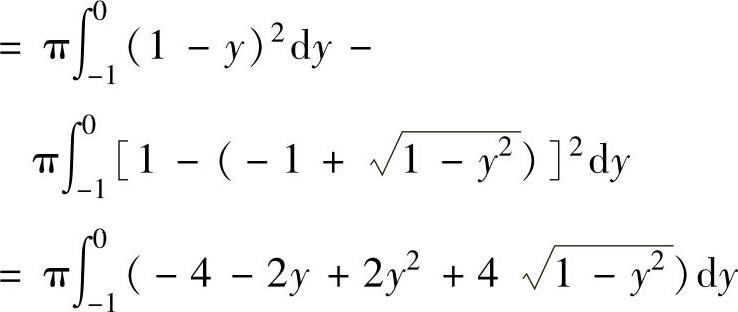
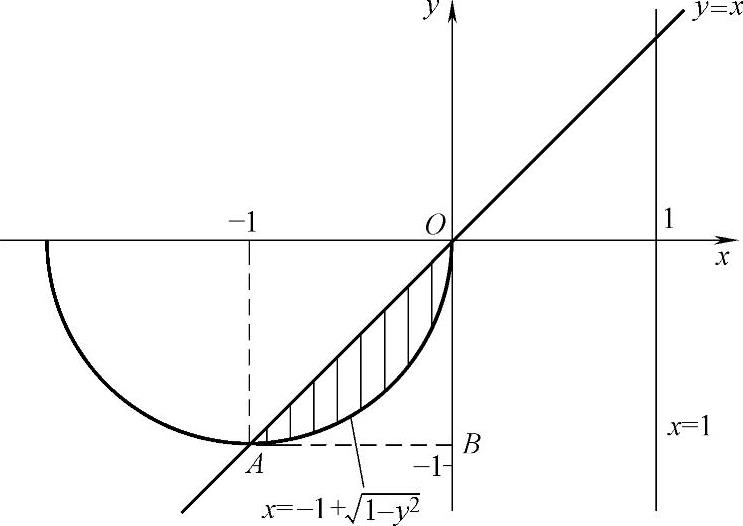
图 2.13.2

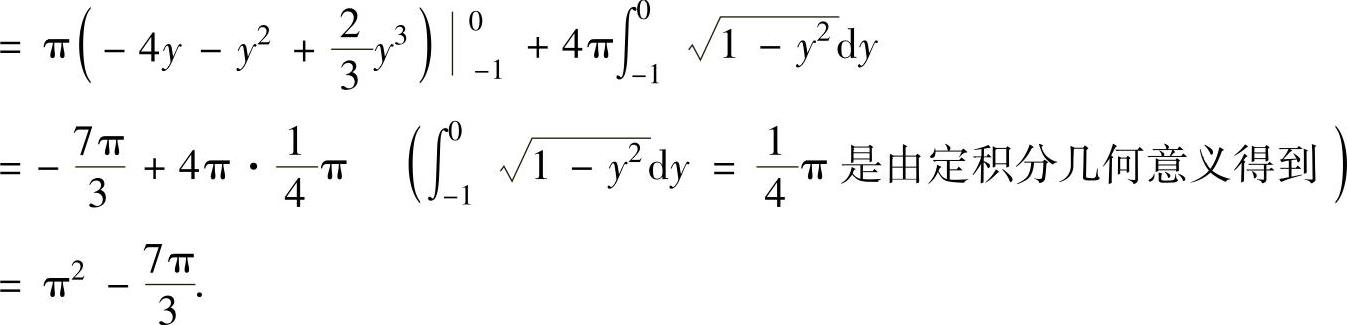
例2.13.3 设由曲线C：8y=12x-x³（0≤x≤2），直线y=2及y轴围成的平面图形为D，求D绕y轴旋转一周而成的旋转体体积V.

精解 C的方程可改写为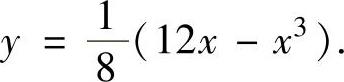由于，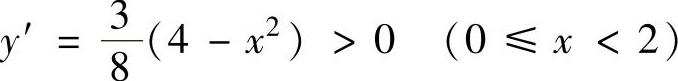

所以C的图形及D的图形如图2.13.3所示.

显然，D是y轴上的曲边三角形，但C的方程不易改写成x=x（y），因此用以下方法计算V.

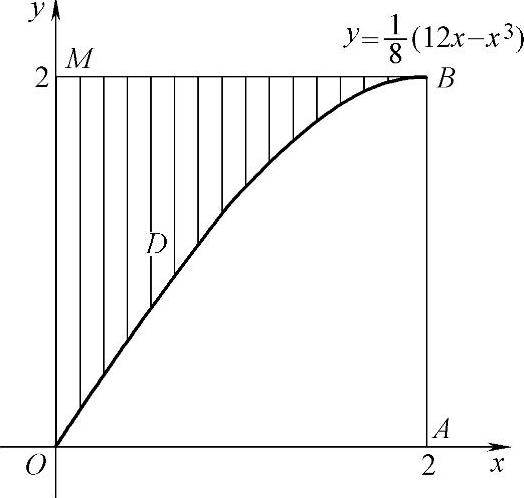
图 2.13.3

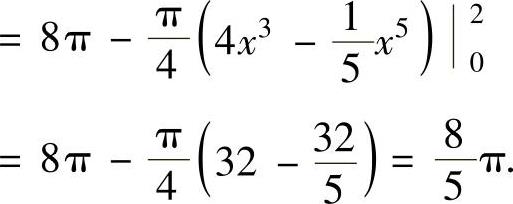
例2.13.4 求由参数方程表示的曲线x=a（t-sint），{_y=a（1-cost）（0≤t≤2π，a>0）与x轴围成的平面图形D绕直线y=2a旋转一周而成的旋转体体积V.

精解 D如图2.13.4中的阴影部分所示，所以

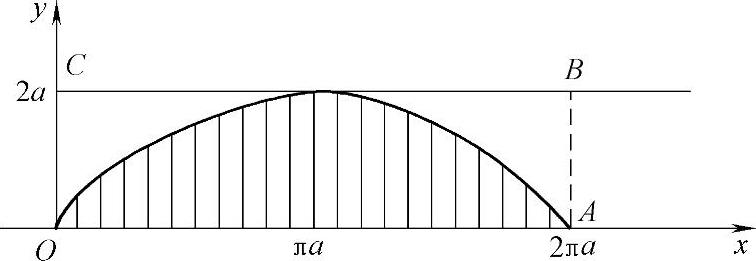
图 2.13.4