二维随机变量的分布函数
【主要内容】
1.二维随机变量分布函数的概念
设(X,Y)是二维随机变量,则称二元函数F(x,y)=P(X≤x,Y≤y)是(X,Y)的分布函数,或x,y的联合分布函数.
二维随机变量分布函数F(x,y)有以下性质:
(1)0≤F(x,y)≤1,
(2)对任意x,y∈(-∞,+∞)有F(x,-∞)=F(-∞,y)=0,特别地,有F(-∞,-∞)=0,此外有F(+∞,+∞)=1,
(3)对任意固定的x,F(x,y)是关于y的单调不减函数;对任意固定的y,F(x,y)是关于x的单调不减函数.
(4)对任意固定的x,F(x,y)是关于y的右连续函数;对任意固定的y,F(x,y)是关于x的右连续函数.
(5)对任意实数x1,x2,y1,y2(其中,x1<x2,y1<y2),有
F(x2,y2)-F(x2,y1)-F(x1,y2)+F(x1,y1)≥0.
(6)当F(x,y)是二维连续型随机变量(X,Y)的分布函数时,它必是二元连续函数,且它与概率密度f(x,y)之间有以下关系.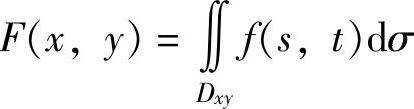 ,其中Dxy={(s,t)s≤x,t≤y}(-∞<x<+∞,-∞<y<+∞).
,其中Dxy={(s,t)s≤x,t≤y}(-∞<x<+∞,-∞<y<+∞).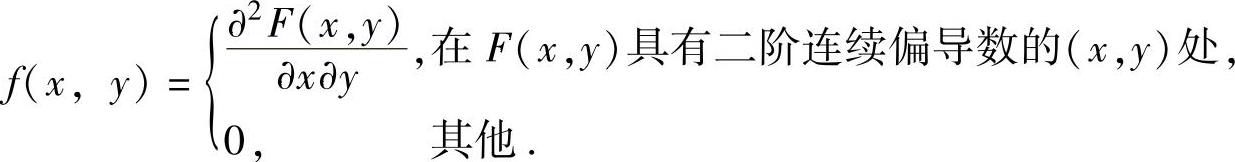
2.二维随机变量的边缘分布函数
设二维随机变量(X,Y)的分布函数为F(x,y)(-∞<x<+∞,-∞<y<+∞),则分别称X,Y的分布函数FX(x),FY(y)为关于X的边缘分布函数和关于Y的边缘分布函数,其中
FX(x)=F(x,+∞)(-∞<x<+∞),FY(y)=F(+∞,y)(-∞<y<+∞).
注 n维随机变量及其分布函数也可类似地定义.
设E是随机试验,则由定义在E的样本空间S上的随机变量X1,X2,…,Xn构成的有序对(X1,X2,…,Xn)称为n维随机变量.
设(X1,X2,…,Xn)是n维随机变量,则称
F(x1,x2,…,xn)=P(X1≤x1,X2≤x2,…,Xn≤xn)为n维随机变量(X1,X2,…,Xn)的分布函数或X1,X2,…,Xn的联合分布函数.
【典型例题】
例7.11.1 (单项选择题)设二维连续型随机变量(X,Y)的分布函数为
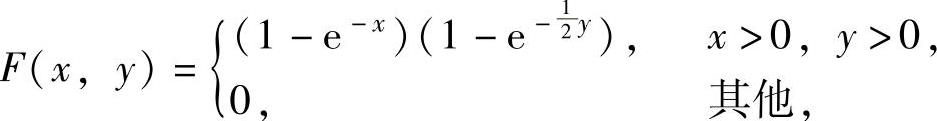
则概率P(Y≤X2)为( ).
A.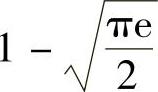 B.
B.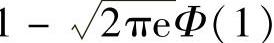
C.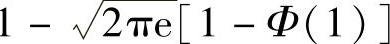 D.
D.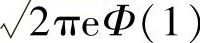
其中Φ(t)是标准正态分布函数.
精解 记D={(x,y)y≤x2},则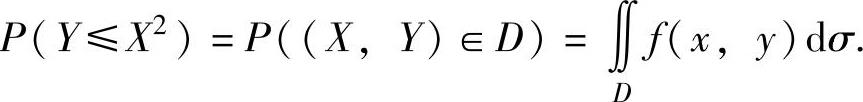 因此
因此
应先算出(X,Y)的概率密度f(x,y).
由于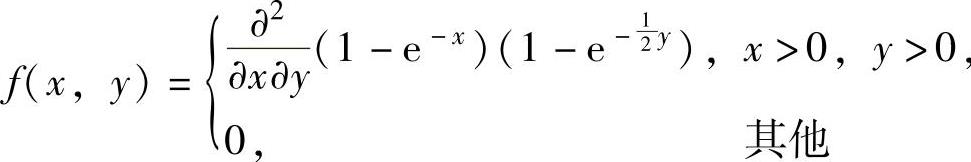
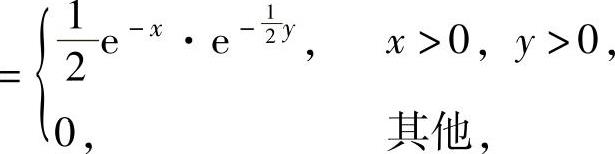
所以,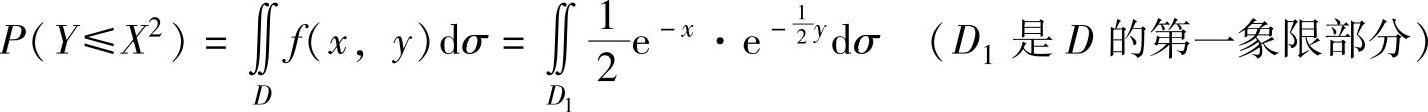
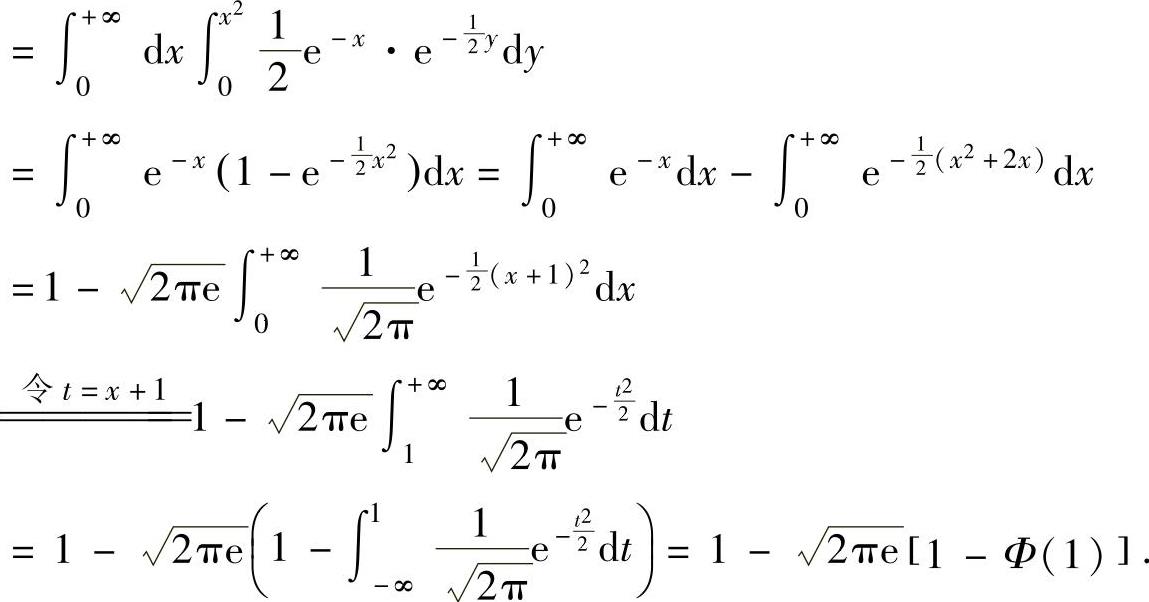
因此本题选C.
例7.11.2 设二维随机变量(X,Y)的分布函数为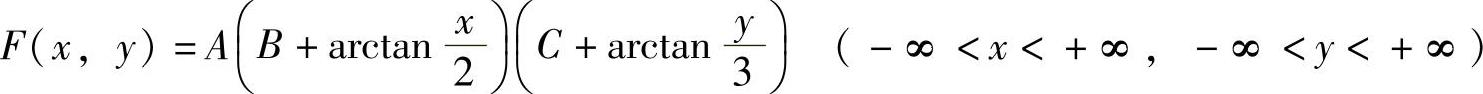 ,(https://www.daowen.com)
,(https://www.daowen.com)
求:(1)常数A,B,C;
(2)(X,Y)的概率密度f(x,y);
(3)概率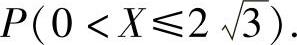
精解 (1)由二维分布函数的性质知,A,B,C应满足下列方程组:
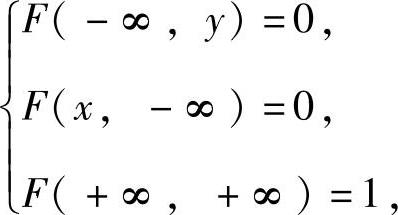
即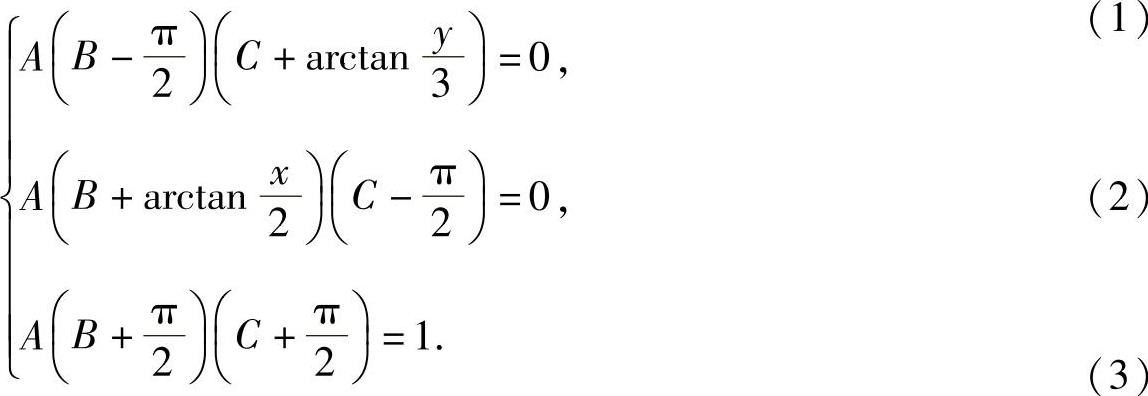
由式(3)知A≠0,因此由式(1)、式(2)得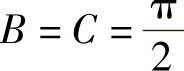 ,将它们代入式(3)得
,将它们代入式(3)得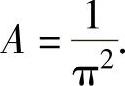
(2)由(1)的计算知
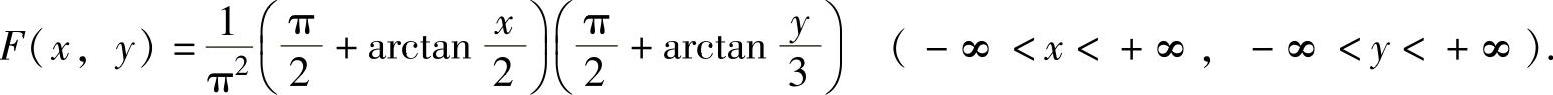
从而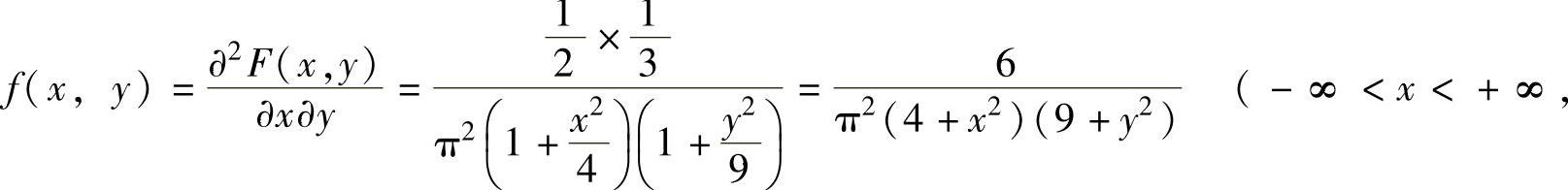 -∞<y<+∞).
-∞<y<+∞).
(3)由于关于X的边缘分布函数为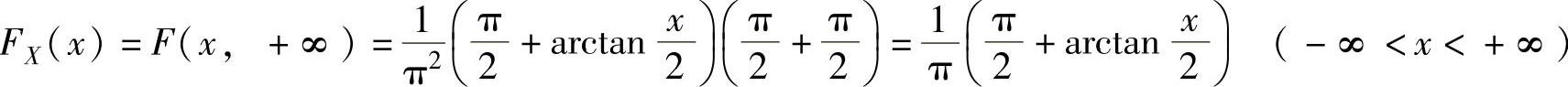 ,
,
所以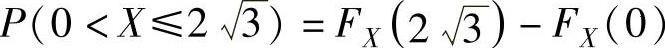
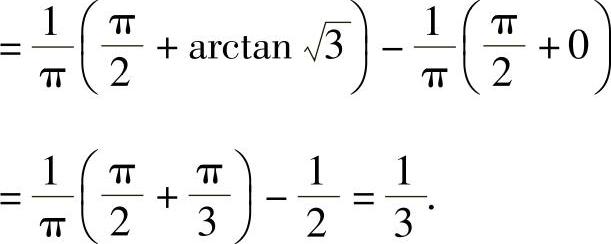
例7.11.3 设事件A,B满足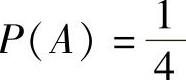 ,
,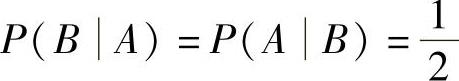 .记随机变量
.记随机变量
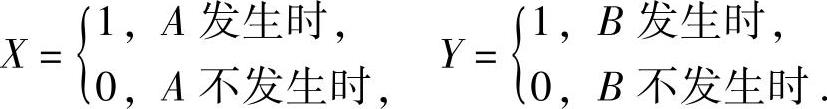
求二维随机变量(X,Y)的分布函数F(x,y).
精解 (X,Y)是二维离散型随机变量,因此先算出它的分布律,再计算分布函数F(x,y).由题设P(BA)=P(AB)可得P(B)=P(A).
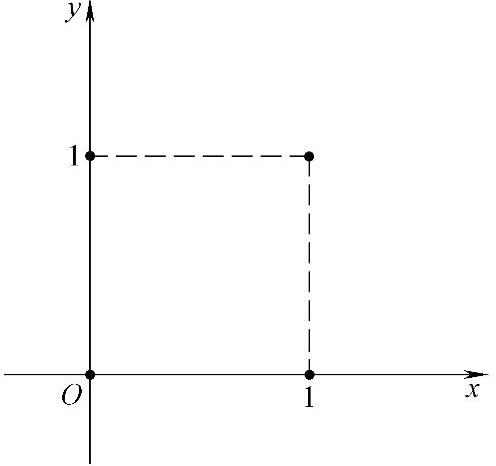
图 7.11.3
(X,Y)全部可能取的值为(0,0),(0,1),(1,0)以及(1,1)(如图7.11.3所示),并且
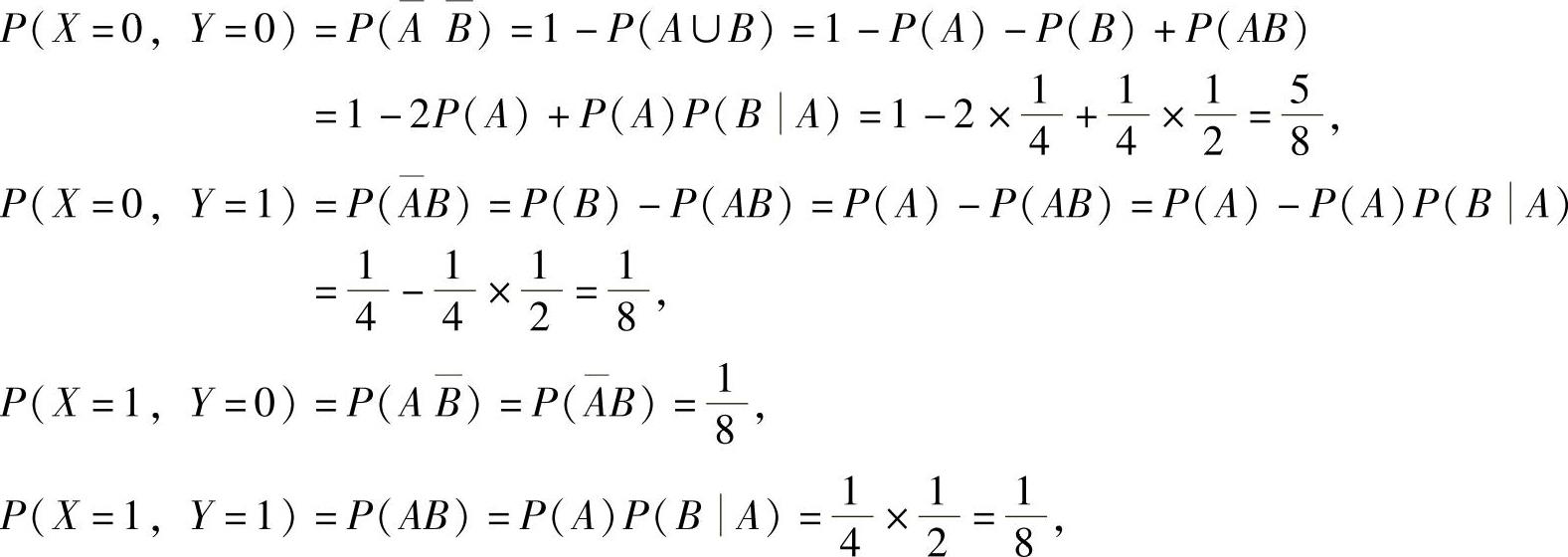
所以,(X,Y)的分布律为
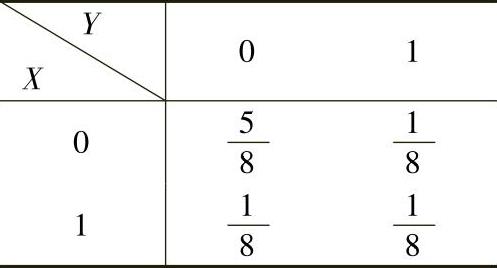
于是由图7.11.3可得(X,Y)的分布函数为
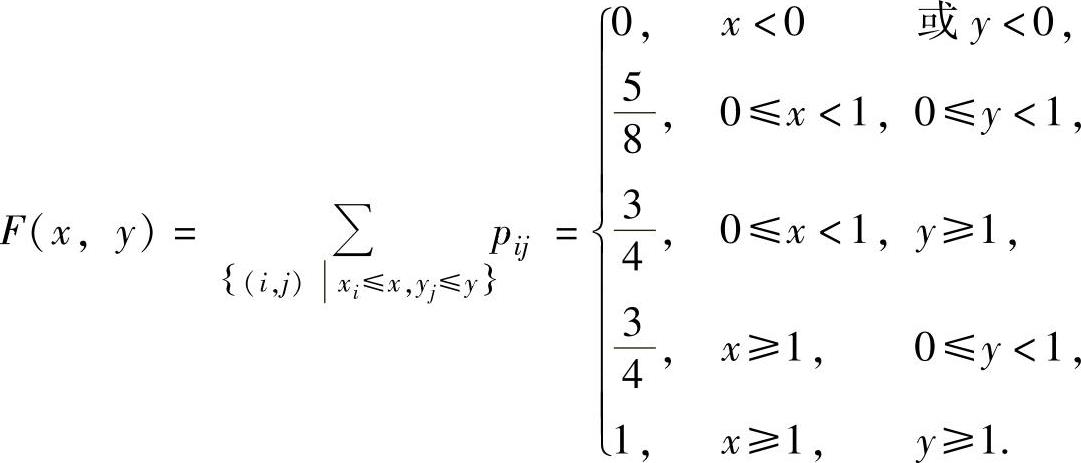
例7.11.4 设二维随机变量(X,Y)的概率密度为
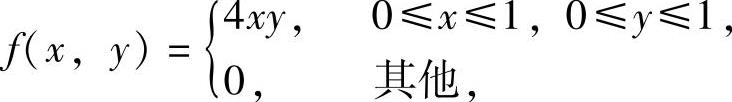
求(X,Y)的分布函数F(x,y).
精解 f(x,y)在正方形区域G={(u,v)0≤u≤1,0≤v≤1}(如图7.11.4阴影部分所示)上取值为4uv,在uOv平面的其他部分取值都为零.
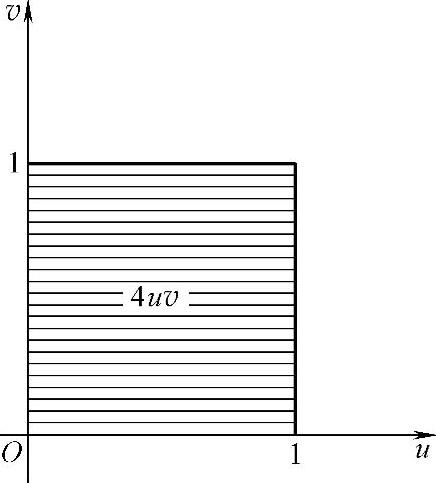
图 7.11.4

