积分中值定理及其应用

八 、积分中值定理及其应用

【主要内容】

1.积分中值定理

设函数f（x）在[a，b]上连续，则存在ξ∈[a，b]，使得

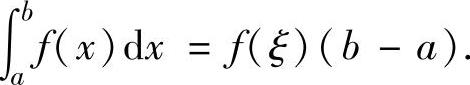
注 （ⅰ）当上述的f（x）是单调函数时，中值ξ∈（a，b）.

（ⅱ）积分中值定理具有以下的推广形式：

设函数f（x）在[a，b]上连续，函数g（x）在[a，b]上可积且不变号，则存在ξ∈[a，b]，使得

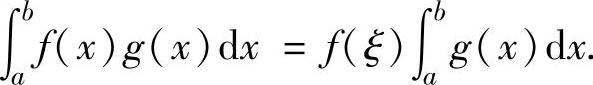
2.积分中值定理的应用

积分中值定理主要用于把抽象函数f（x）的定积分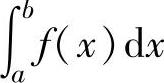转换成f（x）在[a，b]上某点

η处的值与（b-a）之积，即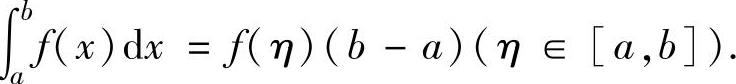这样可以减少积分运算，

使问题的计算或证明变得简单些.

【典型例题】

例2.8.1 设函数f（x）在（-∞，+∞）上有连续导数，求极限

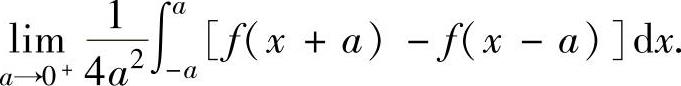
精解 先应用积分中值定理去掉积分运算.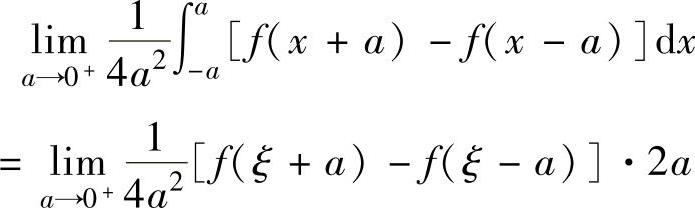（对f（x+a）-f（x-a）在[-a，a]上应用积分中值定理，其中ξ∈[-a，a]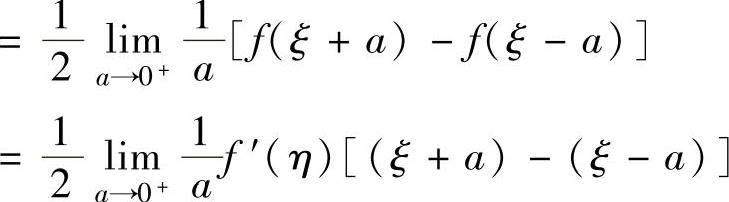）（对f（x）在[ξ-a，ξ+a]上应用拉格朗日中值定理，其中η∈（ξ-a，ξ+a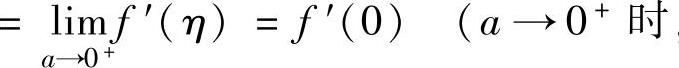）），ξ→0，从而η→0）.

例2.8.2 设函数f（x）在[0，1]上可导，且满足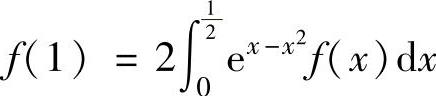，证明：存在ξ∈

（0，1），使得f′（ξ）=（2ξ-1）f（ξ）.(https://www.daowen.com)

精解 本题需作辅助函数，为此将欲证等式中的ξ改为x得

f′（x）=（2x-1）f（x）， 即 e^x-x2f′（x）+e^x-x2（1-2x）f（x）=0.由此得到[e^x-x2f（x）]′=0.故作辅助函数

F（x）=e^x-x2f（x），

则F（x）在[0，1]上可导，且由题设及积分中值定理有，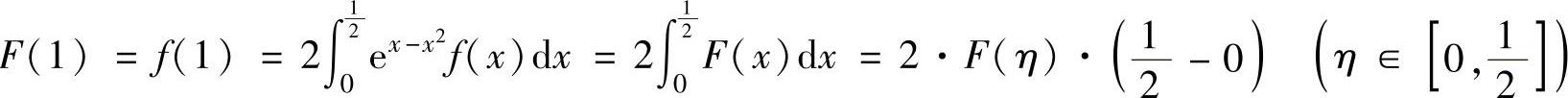

即F（1）=F（η）.所以，对F（x）在[η，1]上应用罗尔定理知，存在ξ∈（η，1）⊂（0，1），使得

F′（ξ）=0， 即 f′（ξ）=（2ξ-1）f（ξ）.

例2.8.3 设函数f（x）在[0，2]上连续，在（0，2）内二阶可导且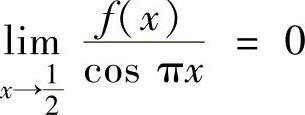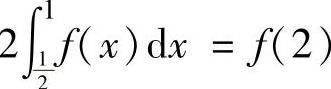，.证明：存在ξ∈（0，2），使得f″（ξ）=0.

精解 由于f（x）在[0，2]上连续，在（0，2）内二阶可导，所以只要在[0，2]上找到不同的两点，使得在这两点处f′（x）的值相等即可，具体证明如下.由题设知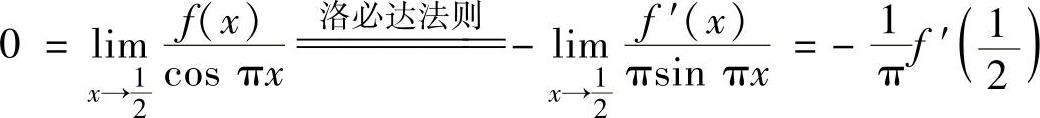，即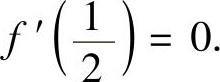

另由题设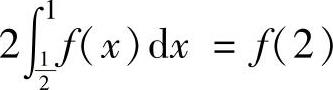及积分中值定理知，存在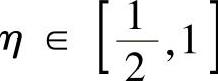，使得f（η）=f（2）.

于是，对f（x）在[η，2]上应用罗尔定理知，存在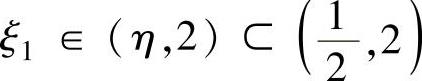，使得f′（ξ₁）=0.

由此可知，f′（x）在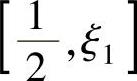上满足罗尔定理条件，从而存在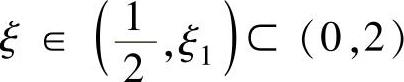，使得f″（ξ）=0.

例2.8.4 设函数f（x）在[0，1]上连续，且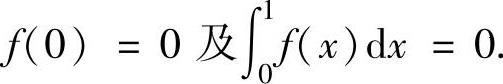证明：存在ξ∈

（0，1），使得∫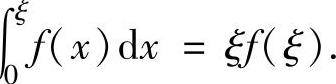

精解 本题需作辅助函数，为此将欲证等式中的ξ改为x得

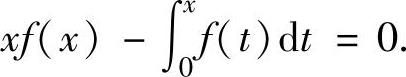
当x∈（0，1）时，上式可改写成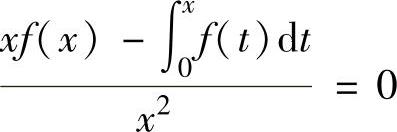，即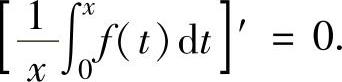

因此作辅助函数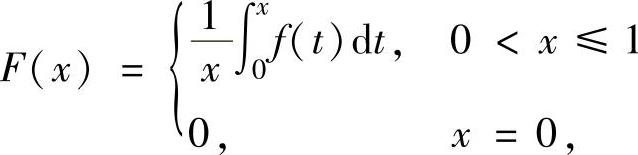，则F（x）在[0，1]上连续，在（0，1）内可

导，且F（0）=F（1）=0，即F（x）在[0，1]上满足罗尔定理条件，所以存在ξ∈（0，1），使得F′（ξ）=0，即