定积分大小的比较与估计方法

七 、定积分大小的比较与估计方法

【主要内容】

1.两个定积分大小的比较方法

设函数f（x）与g（x）在[a，b]上连续.

如果f（x）≤g（x）（x∈[a，b]），则；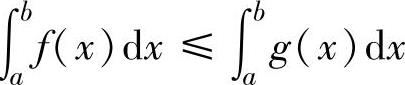

如果f（x）≤g（x）（x∈[a，b]），但至少在[a，b]的某一点处不取等号，则∫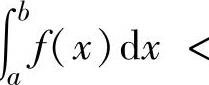

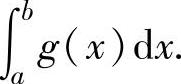
2.定积分值的估计方法当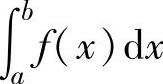不易计算时，则对它进行估计，通常有以下两种方法：

（1）设函数f（x）在[a，b]上连续，且不恒为常数，则，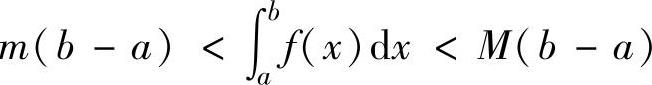

其中，m，M分别为f（x）在[a，b]上的最小值与最大值.

（2）设函数f（x），g（x），h（x）都在[a，b]上连续，且满足g（x）≤f（x）≤h（x） （在[a，b]上存在点x₁，x₂，使得g（x₁）<f（x₁），f（x₂）<h（x₂）），此外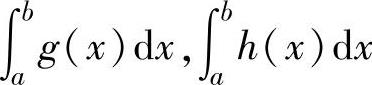比较容易计算，它们的值分别为A，B，则有

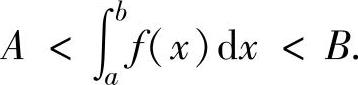
【典型例题】

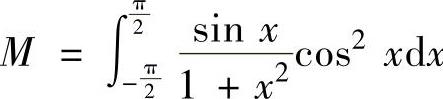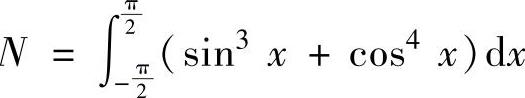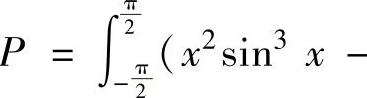
例2.7.1 设，N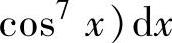，，比较这三个定积分的大小.

精解 由于所给的三个定积分都是对称区间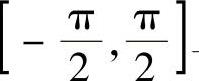上的积分，所以可以利用奇、偶函

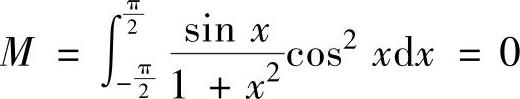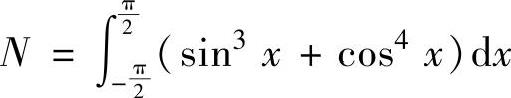
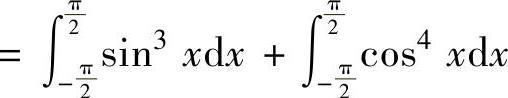
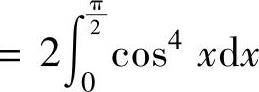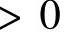
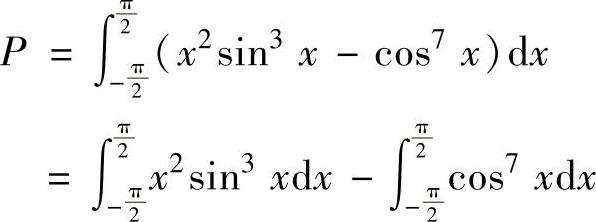
数的定积分性质进行化简和比较.由于（由于被积函数是奇函数），（由于sin³x是奇函数，cos⁴x是偶函数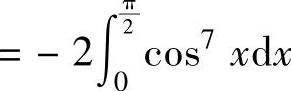）（由于x²sin³x是奇函数，cos⁷x是偶函数）<0，

所以M，N，P有以下的大小关系为：

P<M<N.

例2.7.2 比较下列两个定积分的大小：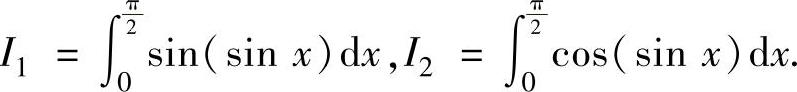

精解 当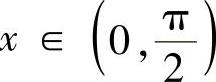时，sinx<x且sinx单调增加，cosx单调减少，所以有sin（sinx）<sinx，cos（sinx）>cosx，

所以，，，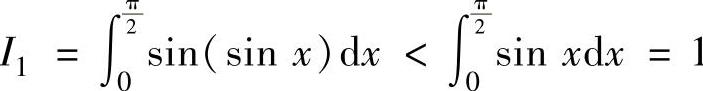

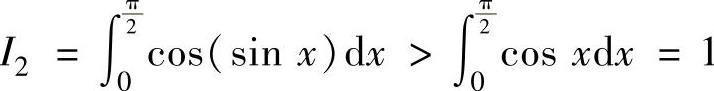由此可知I₁<I2.

例2.7.3 估计定积分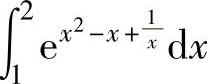的值.

精解 算出被积函数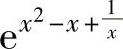在[1，2]上的最小值与最大值，即可得到所给定积分的估计

值.

记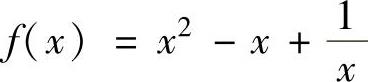，则f（x）在[1，2]上可导且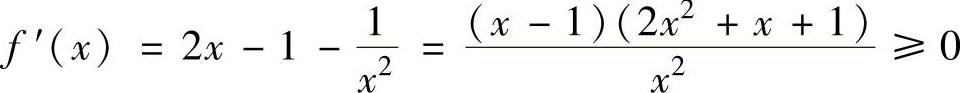（仅在点x=1处取等号），(https://www.daowen.com)

所以f（x）在[1，2]上的最小值为f（1）=1，最大值为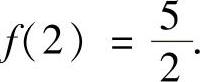由于e^u是关于u的单调增加

函数，所以有

从而，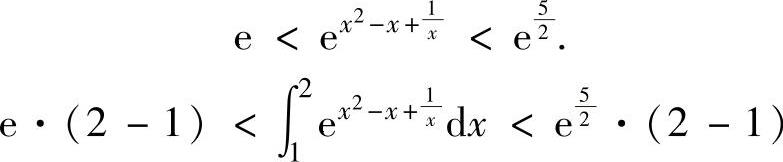

即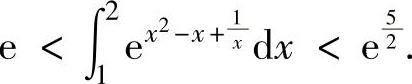

例2.7.4 证明：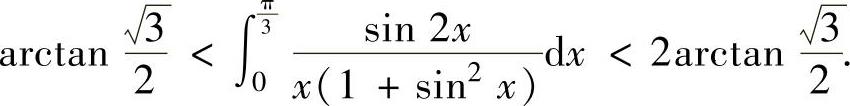

精解 对被积函数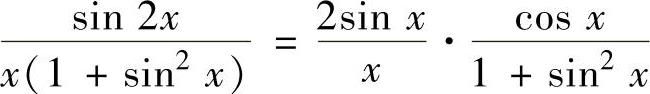作适当的缩小和放大，然后对所给

的定积分进行估计.为此记

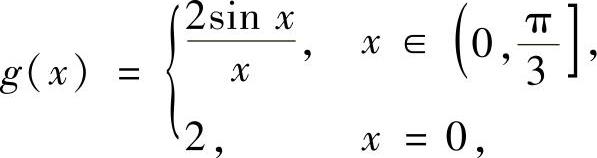
则g（x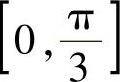）在上连续，在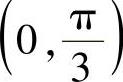内可导且，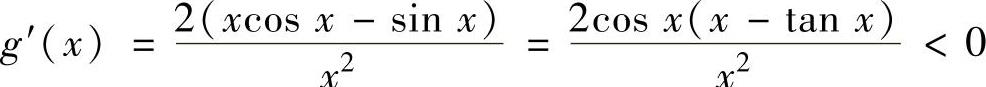

所以g（x）在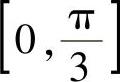上的最小值为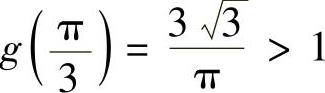，最大值为g（0）=2，即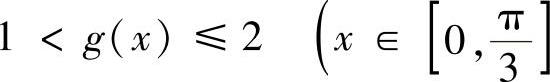（，仅在有限个点处取等号）.

从而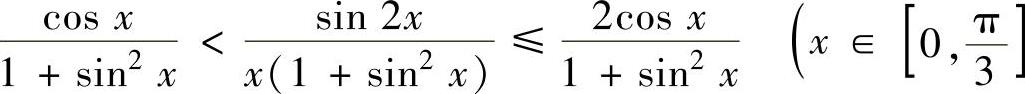（，仅在有限个点处取等号）.

由此得到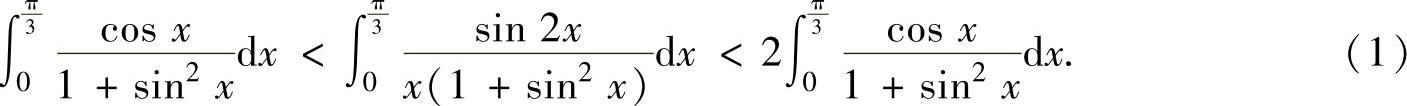

由于∫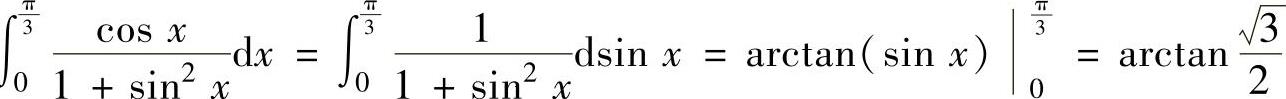，所以将它代入

式（1）得

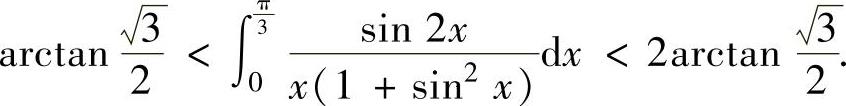
例2.7.5 已知n为正整数，证明：当n充分大时，

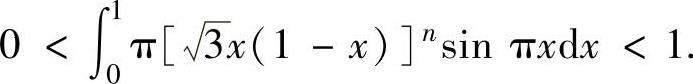
精解 显然，对n=1，2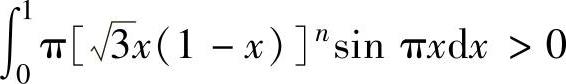，…，成立.下面证明n充分大时有

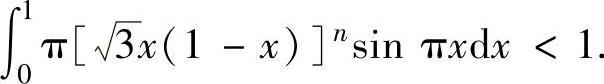
记f（x）=[3x（1-x）]ⁿ，则f（x）在[0，1]上连续，在（0，1）内可导且

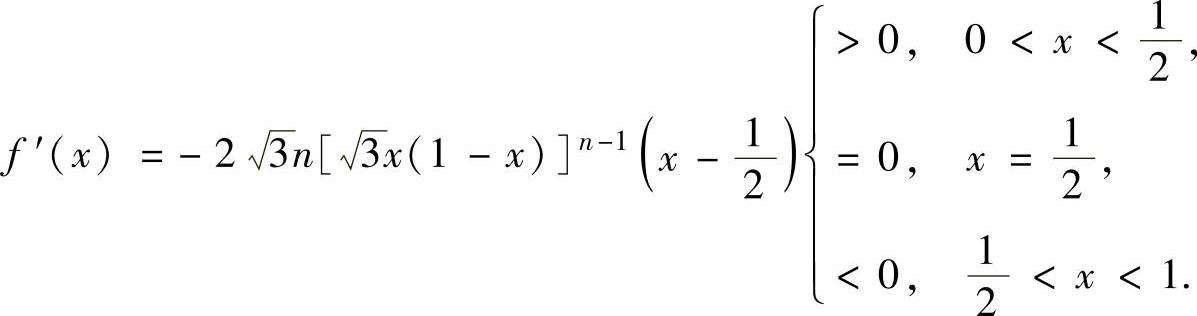
所以，在[0，1]上，f（x）的最大值为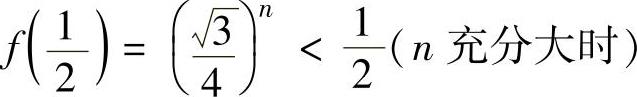.从而

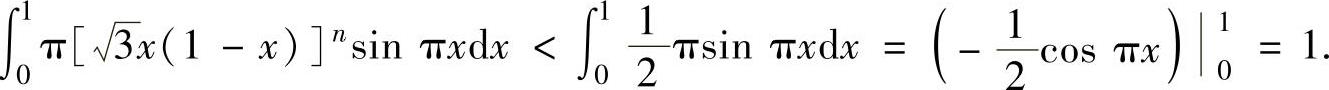
由此证得，当n充分大时有