练习题八
1.单项选择题
(1)设X1,X2,…,Xn(n≥2)是来自总体X~N(0,1)的简单随机样本,X,S2分别是其均值与方差,则( ).
A.nX~N(0,1)B.nS2~χ2(n)
C.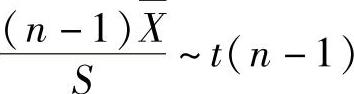 D.
D.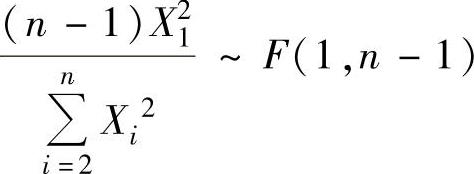
(2)设X1,X2,…,Xn(n>1)是来自总体X(其方差σ2>0)的简单随机样本.记Y=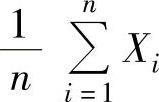 ,则( ).
,则( ).
A.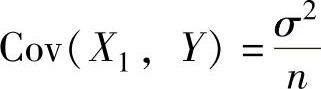 B.Cov(X1,Y)=σ2
B.Cov(X1,Y)=σ2
C.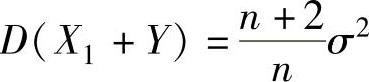 D.
D.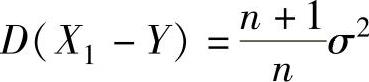
(3)设X~N(μ1,σ2),Y~N(μ2,σ2),它们相互独立,X1,X2,…,Xn1和Y1,Y2,…,Yn2是分别来自总体X和Y的简单随机样本,记它们的均值分别为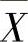 与
与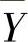 ,则
,则
A.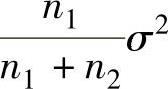 B.
B.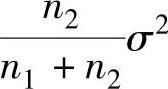
C.σ2D.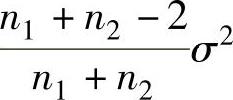
(4)设X1,X2,…,Xn是来自总体X~N(μ,σ2)的样本,其均值为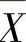 ,记
,记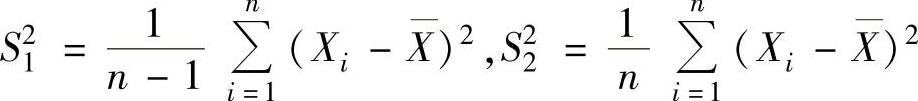 ,
,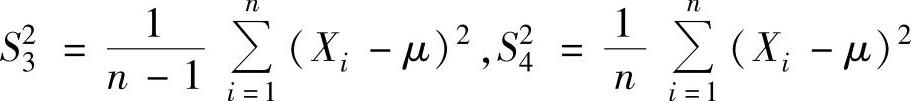 ,则服从t(n-1)分布的随机变量是( ).
,则服从t(n-1)分布的随机变量是( ).
A.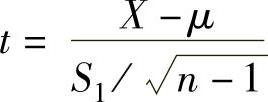 B.
B.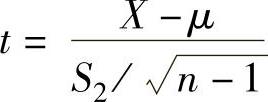
C.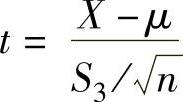 D.
D.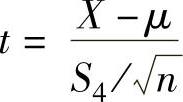
(5)设X1,X2,…,X8和Y1,Y2,…,Y10分别是来自两个相互独立正态总体N(-1,4)和N(2,5)的简单随机样本,S21和S22分别是这两个样本的方差,则服从F(7,9)分布的统计量是( ).
A.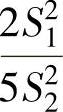 B.
B.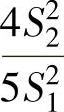
C.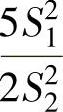 D.
D.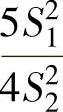
(6)设X~N(a,σ2),Y~N(b,σ2),并且相互独立,分别从总体X和Y各抽取容量为9和11的简单随机样本,记它们的方差为S2X和S2Y,并记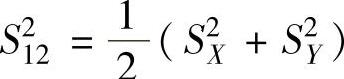 和S2XY=
和S2XY=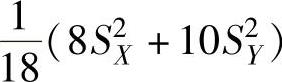 ,则上述4个统计量S2X,S2Y,S212,S2XY中方差最小的是( ).
,则上述4个统计量S2X,S2Y,S212,S2XY中方差最小的是( ).
A.S2X B.S2Y C.S212 D.S2XY(7)设随机变量X1,X2,X3,X4独立同服从N(1,1)分布,且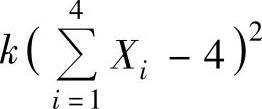 ~χ2(n),则k和n分别为( ).
~χ2(n),则k和n分别为( ).
A.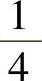 ,1B.
,1B.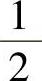 ,1
,1
C.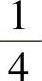 ,4D.
,4D.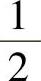 ,4
,4
(8)设总体X的概率密度为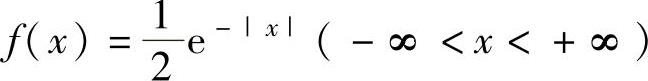 ,X1,X2,…,Xn为总体X的简单随机样本,其方差为S2,则ES2=( ).
,X1,X2,…,Xn为总体X的简单随机样本,其方差为S2,则ES2=( ).
A.0 B.1 C.2 D.4
(9)设随机变量X~F(n,n),记p1=P(X≥1),p2=P(X≤1),则( ).
A.p1<p2 B.p1>p2
C.p1=p2 D.p1,p2大小无法比较
(10)设随机变量T~t(n),对α∈(0,1),tα(n)满足P(T>tα(n))=α,则满足P(T≤b)=α的b为( ).
A.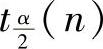 B.
B.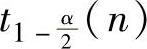
C.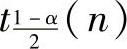 D.
D.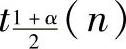
(11)设X1,X2,…,Xn是来自总体X~N(0,σ2)的一个简单随机样本,则统计量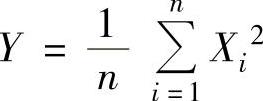 的数学期望与方差分别为( ).
的数学期望与方差分别为( ).
A.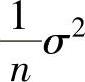 ,
,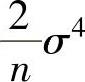 B.
B.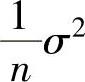 ,
,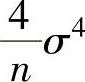
C.σ2,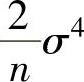 D.σ2,
D.σ2,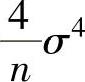
(12)设X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自相互独立的总体X和Y的简单随机样本,其中X~N(μ1,σ2),Y~N(μ2,σ2).记Sw2=(n1-1)S21+(n2-1)S22(S21,S22分别是样本X1,X2,…,Xn1和Y1,Y2,…,Yn2的方差),则( ).
A.ESw2=(n1+n2-2)σ2,DSw2=2(n1+n2-2)σ2
B.ESw2=(n1+n2-1)σ2,DSw2=2(n1+n2-1)σ2
C.ESw2=(n1+n2-2)σ2,DSw2=2(n1+n2-2)σ4
D.ESw2=(n1+n2-1)σ2,DSw2=2(n1+n2-1)σ4
(13)设x1,x2,…,xn是来自总体X~N(μ,σ2)(μ,σ2都未知)的简单随机样本的观察值,x是它的均值,则σ2的最大似然估计值为( ).
A.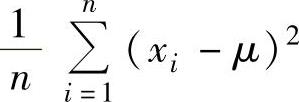 B.
B.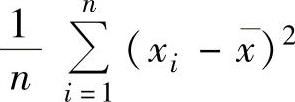 (https://www.daowen.com)
(https://www.daowen.com)
C.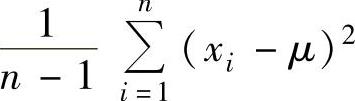 D.
D.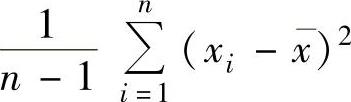
2.解答题
(1)设总体X的概率密度为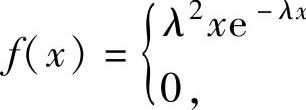
,x>0,
{x≤0,(λ>0),X1,X2,…,Xn为总体X的简单随机样本,其样本方差为S2,求ES2.
(2)设总体X的概率密度为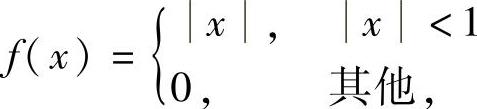 ,X1,X2,…,X50为取自总体X的一个简单随机样本,其均值为X,用独立同分布中心极限定理计算概率P(X>0.2).
,X1,X2,…,X50为取自总体X的一个简单随机样本,其均值为X,用独立同分布中心极限定理计算概率P(X>0.2).
(3)设X和Y是两个独立的服从标准正态分布的总体,X1,X2,…,X8和Y1,Y2,…,Y9是分别来自X和Y的简单随机样本,它们的均值分别为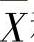 和
和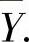 记
记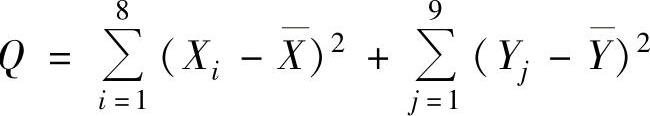 ,
,
证明: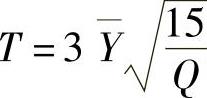 服从自由度为15的t分布.
服从自由度为15的t分布.
(4)设总体X~N(12,4),X1,X2,…,Xn是来自X的简单随机样本,求:
(ⅰ)n=5时样本均值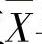 与总体数学期望之差绝对值大于1的概率;
与总体数学期望之差绝对值大于1的概率;
(ⅱ)概率P(max{X1,X2,…,X5}>15).
(5)设X和Y是相互独立的两个总体,X~N(0,4),Y~N(0,9),X1,X2,…,X10
以及Y1,Y2,…,Y15是分别来自X和Y的简单随机样本,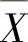 ,
,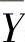 Y是它们的均值.求
Y是它们的均值.求
(ⅰ)统计量X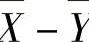 Y所服从的分布;
Y所服从的分布;
(ⅱ)EX-Y和DX-Y.
(6)设X1,X2是来自总体X~N(μ,σ2)的简单随机样本,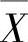 和S2分别为样本的均值与
和S2分别为样本的均值与
方差,证明: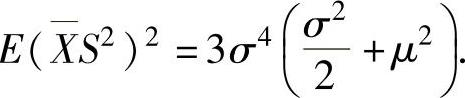
(7)设X1,X2,…,Xn(n>2)是来自总体X~N(0,1)的简单随机样本,其均值为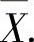 记
记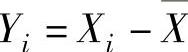 ,i=1,2,…,n.求
,i=1,2,…,n.求
(ⅰ)DYi(i=1,2,…,n);
(ⅱ)Cov(Y1,Yn).
(8)设某信息台在上午8:00~9:00之间接到的呼叫次数X服从参数为λ(未知)的泊松分布.现收集了42个数据,整理后得表如下:

据此数据求λ的最大似然估计值.
(9)设总体X的概率密度为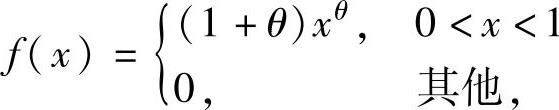 ,其中θ>-1是未知参数,
,其中θ>-1是未知参数,
X1,X2,…,Xn是来自总体X的简单随机样本.求θ的矩估计量与最大似然估计量.
(10)设总体X的概率密度为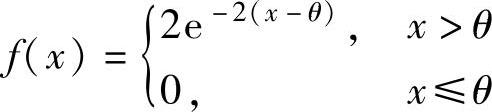
,
{,其中θ>0是未知参数.现从X中抽取简单随机样本X1,X2,…,Xn,记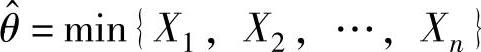 .
.
(ⅰ)求X的分布函数F(x);
(ⅱ)求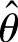 的分布函数
的分布函数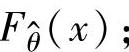
(ⅲ)求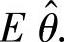
(11)设总体X的概率密度为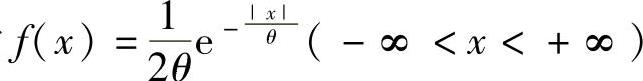 ,其中,θ>0是未知参数,X1,X2,…,Xn是来自X的简单随机样本.
,其中,θ>0是未知参数,X1,X2,…,Xn是来自X的简单随机样本.
(ⅰ)求θ的最大似然估计量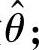
(ⅱ)求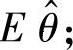
(ⅲ)求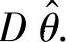
(12)设X1,X2,…,Xn是来自总体X的简单随机样本,其中X服从均值为θ的指数分布.证明:参数θ的最大似然估计量θ^近似地服从