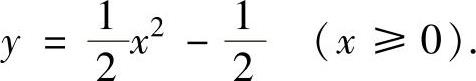变量可分离微分方程、齐次微分方程的求解

一 、变量可分离微分方程 、齐次微分方程的求解

【主要内容】

1.微分方程的概念

含有自变量x，未知函数y及其导数（其中未知函数的导数必出现）的方程称为常微分方程（简称微分方程），其中，未知函数导数的最高阶数称为该微分方程的阶.

如果将函数y=φ（x）代入微分方程后成为恒等式，则称y=φ（x）是该微分方程的解；如果由Φ（x，y）=0确定的隐函数y=φ（x）是微分方程的解，则称Φ（x，y）=0是该微分方程的隐解.如果函数y=φ（x，C₁，C₂，…，C_n）（其中，C₁，C₂，…，C_n是n个独立的任意常数）是n阶微分方程的解，则称其为该n阶微分方程的通解.如果由初始条件确定了y=φ（x，C₁，C₂，…，C_n）中的C₁，C₂，…，C_n的值，则称其为该微分方程的特解.

一阶微分方程的一般形式是F（x，y，y′）=0（其中y′必定出现），标准形是y′=f（x，y）.一阶微分方程是指变量可分离微分方程、齐次微分方程、一阶线性微分方程（包括伯努利方程）.

2.变量可分离微分方程形如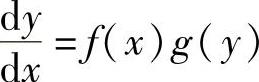（其中，f（x），g（y）是已知函数）的微分方程称为变量可分离微分方

程，它的通解为

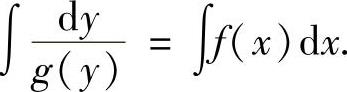
3.齐次微分方程

形如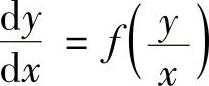（其中f（u）是已知函数）的微分方程称为齐次微分方程.

令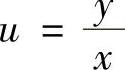，则原微分方程成为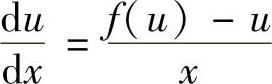，它是以u为未知函数的变量可分离微分方程.

【典型例题】

例4.1.1 （单项选择题）微分方程y′sinx=ylny满足条件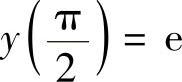的特解为（ ）.

A.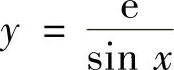B.y=esinxC.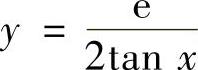D.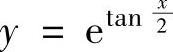

精解 容易验证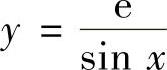，y=e^sinx都不满足所给微分方程，所以A，B两个选项都不能

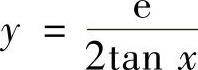选，另外，在点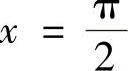处没有定义，所以也不能选C.

因此本题选D.

例4.1.2 求微分方程（e^x+y-e^x）dx+（e^x+y+e^y）dy=0的通解.

精解 所给微分方程可以改写成e^y（e^x+1）dy=-e^x（e^y-1）dx （变量可分离微分方程）

即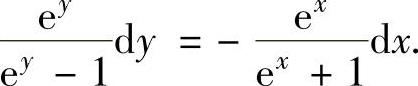

上式两边分别积分得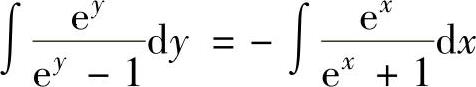，即ln（e^y-1）=-ln（e^x+1）+lnC，

所以所给微分方程的通解为（e^x+1）（e^y-1）=C.

例4.1.3 求微分方程（lnx-lny-1）ydx+xdy=0的通解.

精解 所给微分方程可以改写为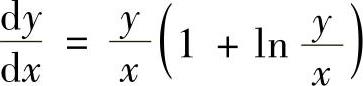（齐次微分方程）（1）令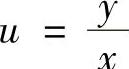，则式（1）成为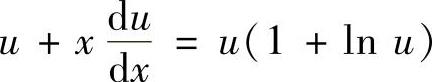，即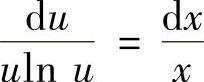（变量可分离微分方程）.

它的通解为ln（lnu）=lnx+lnC，即u=e^Cx，从而原微分方程的通解为y=xe^Cx.

例4.1.4 求微分方程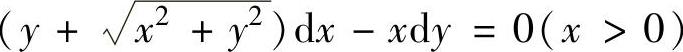的满足初始条件y_x=1=0的特解.

精解 先算出所给微分方程的通解，再由初始条件确定通解中任意常数的值.

所给微分方程可以改写成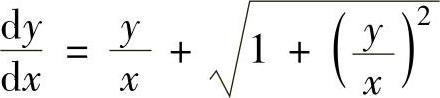（齐次微分方程）（1）

令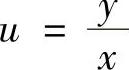，则式（1）成为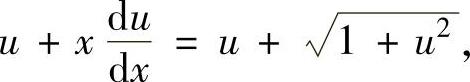即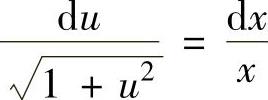（变量可分离微分方程）.

它的通解为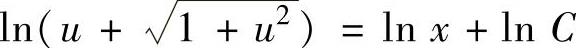，即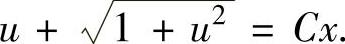于是原微分方程的通解为

由初始条件y_x=1=0得式（2）中的C=1.所以所给微分方程满足初始条件y_x=1=0的特解为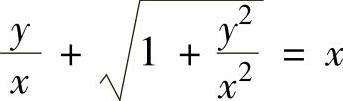，即