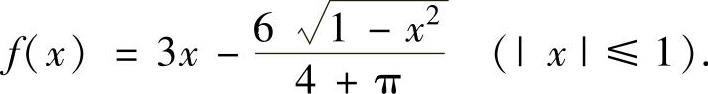定积分的概念及其计算方法
【主要内容】
1.定积分的概念
设函数f(x)在[a,b]上有界,在[a,b]上任意插入n-1个分点
a=x0<x1<x2<…<xn-1<xn=b,把[a,b]分成n个小区间
[x0,x1],[x1,x2],…,[xn-1,xn],
它们的长度对应地记为Δx1,Δx2,…,Δxn,并在每个小区间上任取一点ξ1,ξ2,…,ξn.若无论上述x1,…,xn和ξ1,…,ξn如何取,极限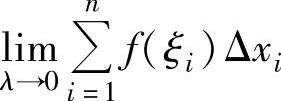 (其中,λ=max{Δx1,Δx2,…,Δxn})
(其中,λ=max{Δx1,Δx2,…,Δxn})
总是存在且相等,则称f(x)在[a,b]上可积,称这个极限值为f(x)在[a,b]上的定积分,记为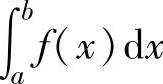 ,并定义:
,并定义:
当a>b时,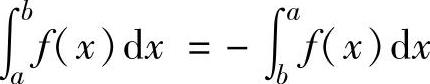 ;当a=b时,
;当a=b时,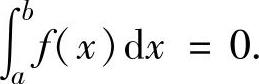
注 (ⅰ)f(x)在[a,b]上可积的充分条件
当函数f(x)在[a,b]上连续,或在[a,b]上只有有限个第一类间断点,或在[a,b]上单调有界时,f(x)在[a,b]上可积.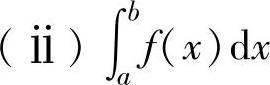 的几何意义
的几何意义
如果f(x)在[a,b]上为非负函数,则当它可积时,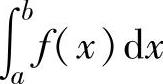 表示由曲线y=f(x),直线x=
表示由曲线y=f(x),直线x=
a,x=b以及x轴围成的曲边梯形的面积.
例如,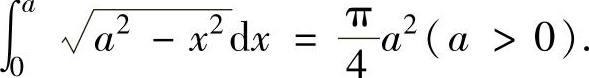
2.定积分的计算方法
定积分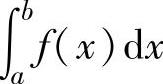 的计算可按牛顿-莱布尼茨公式、定积分性质和换元积分法、分部积分法进行.
的计算可按牛顿-莱布尼茨公式、定积分性质和换元积分法、分部积分法进行.
(1)牛顿-莱布尼茨公式
设函数f(x)在[a,b]上连续,F(x)是f(x)的一个原函数,则
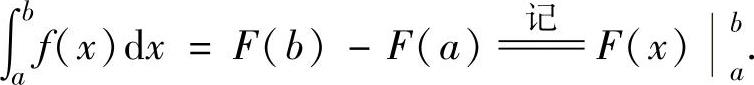
(2)定积分性质
设f(x),g(x)都是[a,b]上的可积函数,k为常数,则
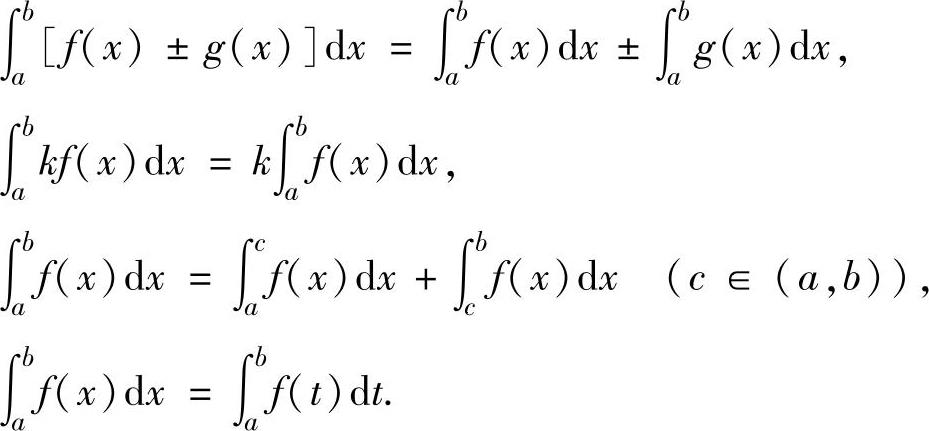
(3)换元积分法
换元积分法:设函数f(x)在[a,b]上连续,函数x=φ(t)满足:
1)φ(α)=a,φ(β)=b;
2)φ(t)在[α,β](或[β,α])上有连续的导数;
3)当t从α连续变化到β时,φ(t)从a连续变化到b,则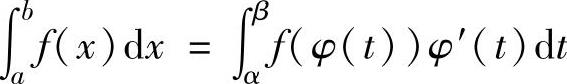 或
或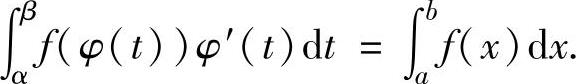
(4)分部积分法
设函数u(x),v(x)在[a,b]上有连续的导数,则
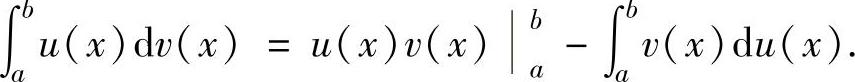
【典型例题】
例2.4.1 求定积分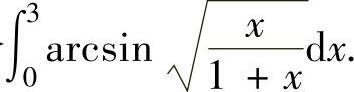
精解 由于被积函数很复杂,故将其代换为t,即令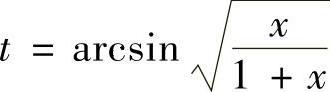 ,则x=tan2t.于是(https://www.daowen.com)
,则x=tan2t.于是(https://www.daowen.com)
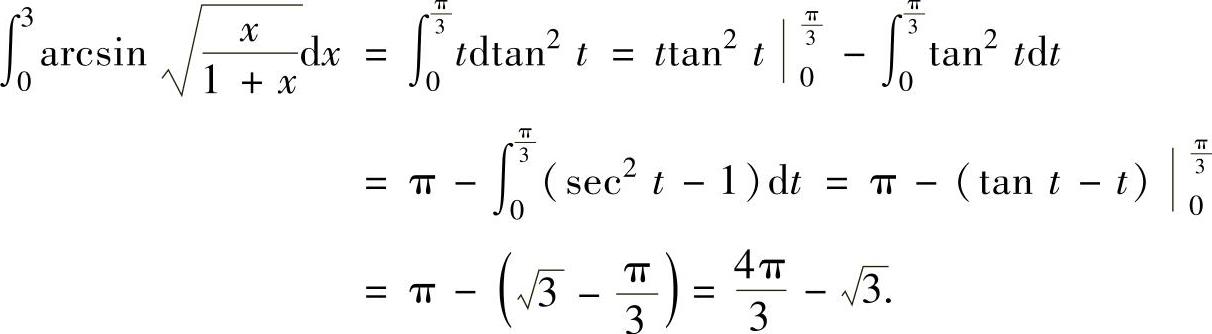
例2.4.2 求定积分∫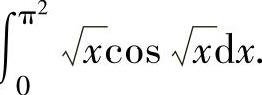
精解 先作变量代换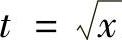 ,再用分部积分法计算.
,再用分部积分法计算.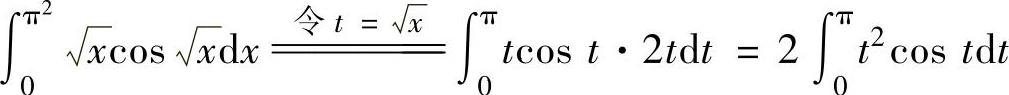 ,
,
取u(t)=t2,则由dv(t)=costdt=dsint得v(t)=sint,所以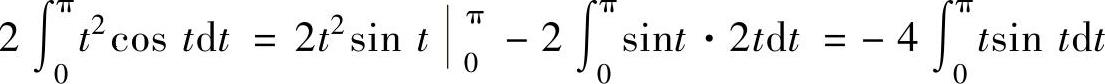 ,
,
取u1(t)=t,则由dv1(t)=sintdt=d(-cost)得v1(t)=-cost,所以
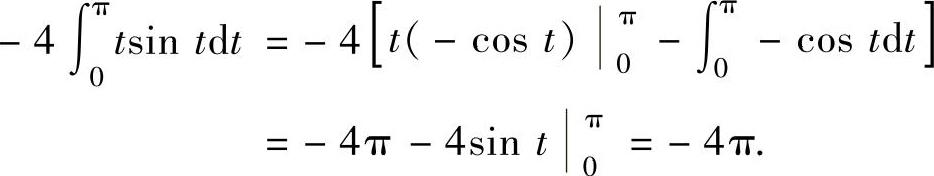
由此得到
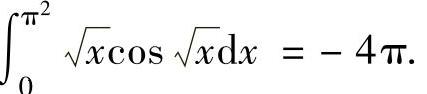
注 本题的计算过程可以写得紧凑一些,具体如下:
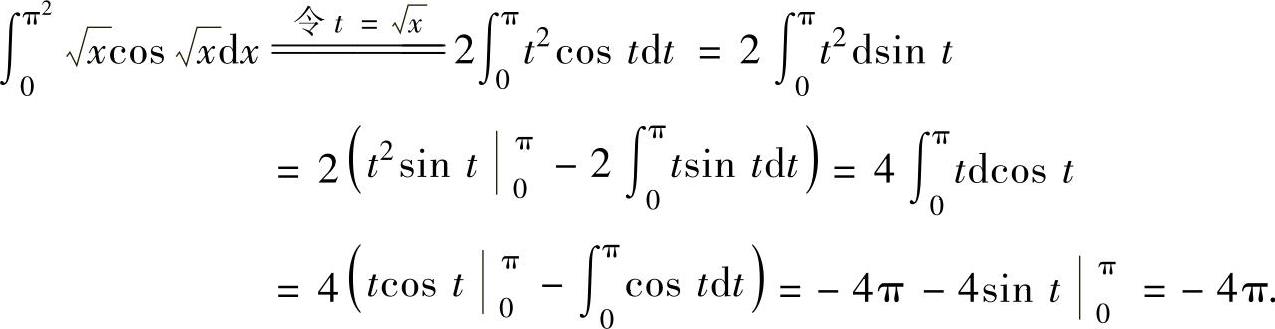
例2.4.3 求定积分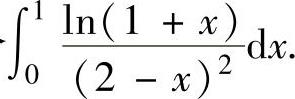
精解 用分部积分法计算所给的定积分,其中,取u(x)=ln(1+x),则由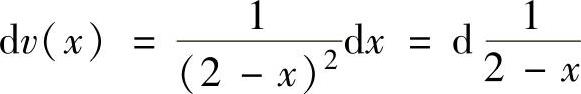 得
得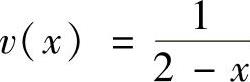 ,所以
,所以
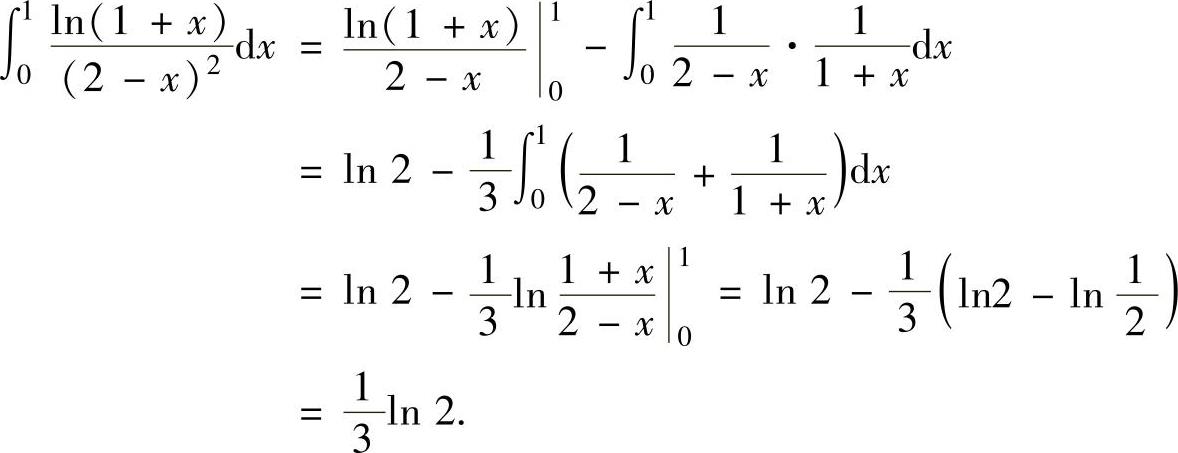
例2.4.4 设函数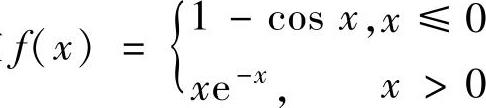 ,,求∫
,,求∫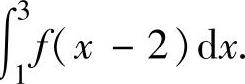
精解 根据f(x)的定义,应先作变量代换t=x-2,然后计算定积分.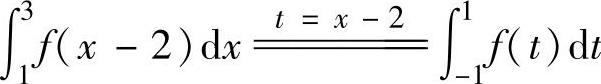
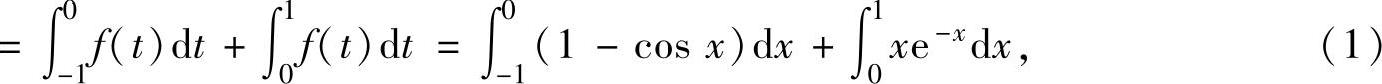
其中,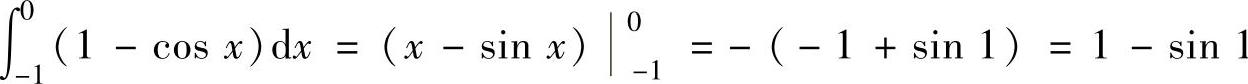 ,
,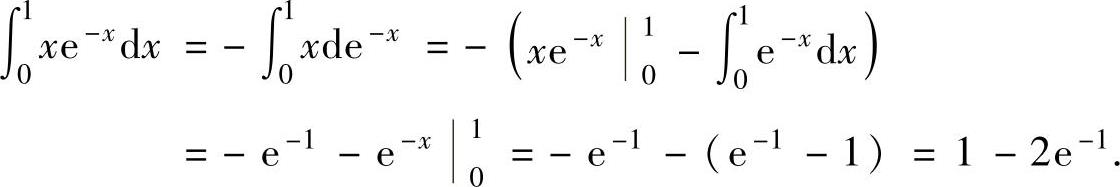
将它们代入式(1)得
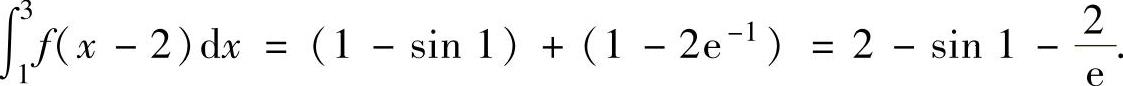
例2.4.5 设函数f(x)在(-∞,+∞)上满足f(x)=f(x-π)+sinx,且f(x)=x,x∈[0,π),求定积分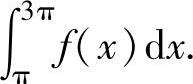
精解 先按题设写出f(x)在[π,3π]上的分段表达式,然后计算所给的定积分.由题设知,x∈[π,2π)时,f(x)=f(x-π)+sinx=(x-π)+sinx=x-π+sinx,x∈[2π,3π)时,f(x)=f(x-π)+sinx=[(x-π)-π+sin(x-π)]+sinx=x-2π,此外,f(3π)=f(3π-π)+sin3π=f(2π)=2π-2π=0,
所以,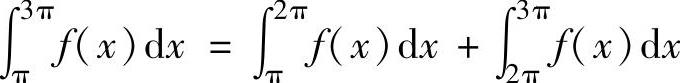
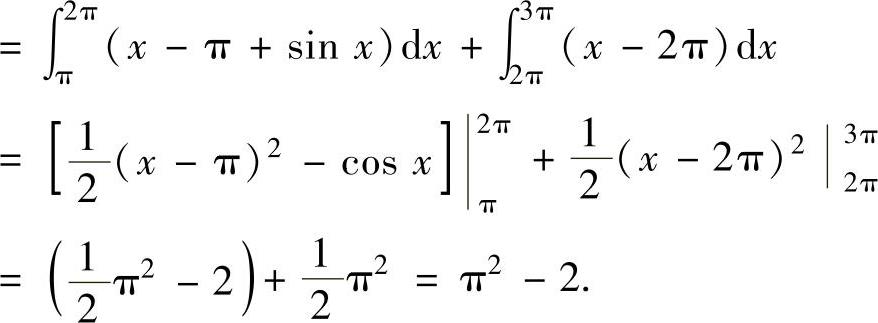
例2.4.6 设连续函数f(x)满足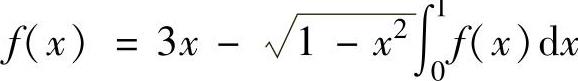 ,求f(x)的表达式.
,求f(x)的表达式.
精解 由于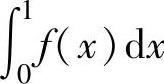 是常数,记其为A,则f(x)满足的等式变为
是常数,记其为A,则f(x)满足的等式变为

式(1)两边从0到1积分得
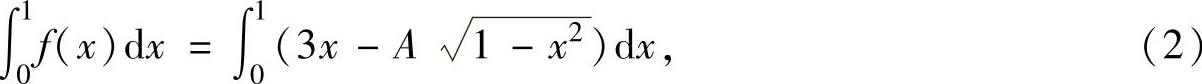
其中,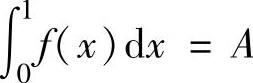 ,
,
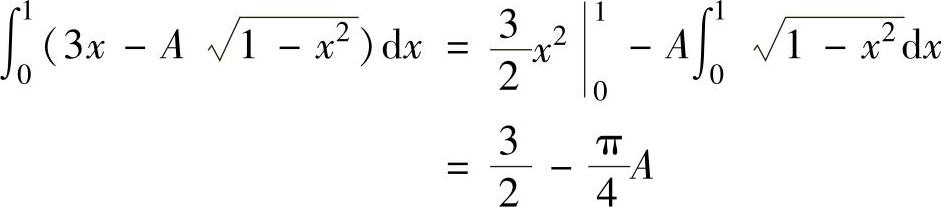
(这里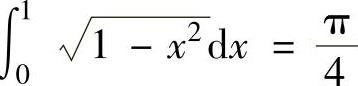 是利用定积分的几何意义得到的).
是利用定积分的几何意义得到的).
将它们代入式(2)得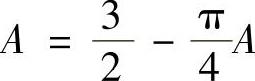 ,即
,即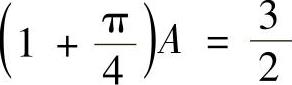 ,
,
所以, 将它代入式(1)得
将它代入式(1)得