练习题五
1.单项选择题
(1)四阶行列式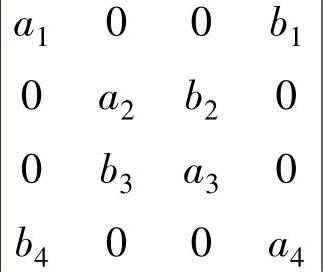 的值等于( ).
的值等于( ).
A.a1a2a3a4-b1b2b3b4 B.a1a2a3a4+b1b2b3b4
C.(a1a2-b1b2)(a3a4-b3b4) D.(a2a3-b2b3)(a1a4-b1b4)
(2)设α1,α2,α3,β1,β2都是4维列向量,且四阶行列式|(α1,α2,α3,β1)|=m,|(α1,α2,β2,α3)|=n,则四阶行列式|(α3,α2,α1,β1+β2)|=( ).
A.m+n B.-(m+n) C.n-m D.m-n
(3)设a,b,c是两两互不相等的实数,则
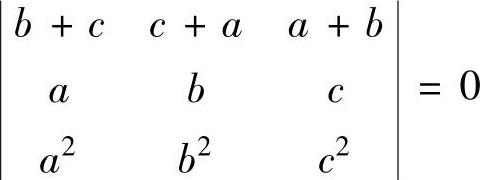
的充分必要条件是( ).
A.ab=0 B.a+b+c=0
C.a=1,b=-1,c=0 D.a2=b2,c=0
(4)设A,B,C都是n阶矩阵,如果AB=BA,AC=CA,则ABC=( ).
A.ACB B.CBA C.BCA D.CAB
(5)设n阶矩阵A满足(A-En)2=3(A+En)2,则以下4个结论中正确结论的个数是( ).
(ⅰ)A可逆;
(ⅱ)A+En可逆;
(ⅲ)A+2En可逆;
(ⅳ)A+3En可逆.
A.1 B.2 C.3 D.4
(6)设三阶矩阵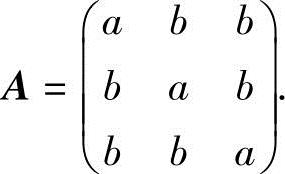 如果A的伴随矩阵的秩为1,则必有( ).
如果A的伴随矩阵的秩为1,则必有( ).
A.a=b或a+2b=0 B.a=b或a+2b≠0
C.a≠b且a+2b=0 D.a≠b且a+2b≠0
(7)设A,P都是三阶矩阵,且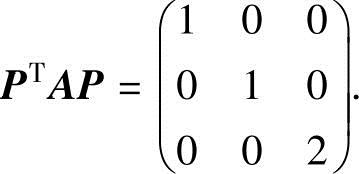 若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则QTAQ=( ).
若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则QTAQ=( ).

(8)设α为3维列向量,且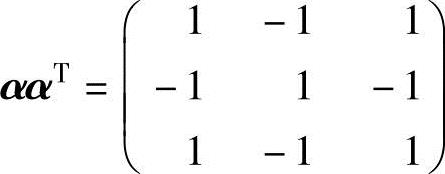 ,则αTα=( ).
,则αTα=( ).
A.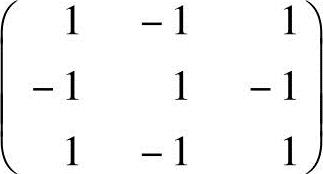 B.
B.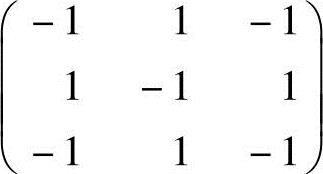 C.3 D.-3
C.3 D.-3
(9)设A是m×n矩阵,且m<n,则以下4个式子中正确的是( ).
A.|AAT|=0 B.|AAT|≠0 C.|ATA|=0 D.|ATA|≠0
(10)设A,B分别为m×n与n×m矩阵,且AB=Em,则以下4个结论中正确的是( ).
A.r(A)=m,r(B)=m B.r(A)=m,r(B)=n
C.r(A)=n,r(B)=m D.r(A)=n,r(B)=n
(11)设A是三阶矩阵,将A的第2行加到第1行得到B,将B的第1列的-1倍加到第2列得到C.记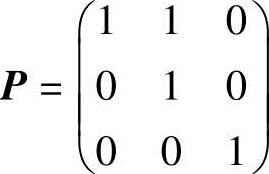 ,则( ).
,则( ).
A.C=P-1AP B.C=PAP-1 C.C=PTAP D.C=PAPT
(12)设A是n(n≥2)阶可逆矩阵,A∗是它的伴随矩阵,则( ).
A.(A∗)∗=|A|n-1A B.(A∗)∗=|A|n+1A
C.(A∗)∗=|A|n-2A D.(A∗)∗=|A|n+2A
(13)设A,B都是n阶非零矩阵,且AB=On,则r(A),r(B)( ).
A.必有一个为零 B.都小于n
C.一个小于n,另一个等于n D.两个都等于n
(14)设α,β,γ1,γ2,γ3都是4维列向量,矩阵A=(α,γ1,γ2,γ3),B=(β,γ1,γ2,γ3),则当|A|=3,|B|=2时,|A+B|=( ).
A.5 B.20 C.30 D.40
(15)设A是五阶矩阵,且|A|=3,则|2A-1-A∗|=( ).
A.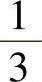 B.
B.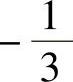 C.3 D.-3
C.3 D.-3
(16)设n阶矩阵A,B,C满足关系式ABC=En,则有( ).
A.ACB=En B.CBA=En C.BAC=En D.BCA=En
(17)设A,B都是二阶矩阵,且|A|=2,|B|=3,则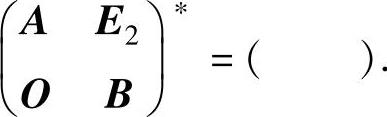
A.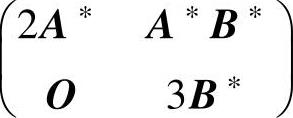 B.
B.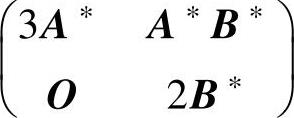
C.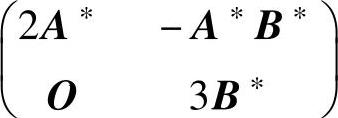 D.
D.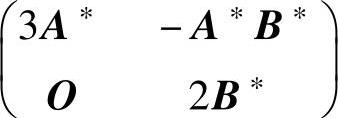
(18)设A,B为满足AB=O的任意两个非零矩阵,则( ).
A.A的列向量组线性相关,B的行向量组线性相关
B.A的列向量组线性相关,B的列向量组线性相关
C.A的行向量组线性相关,B的行向量组线性相关
D.A的行向量组线性相关,B的列向量组线性相关
(19)设向量组α1,α2,α3线性无关,向量β1可由α1,α2,α3线性表示,而向量β2不能由α1,α2,α3线性表示,则对任意常数k,必有( ).
A.α1,α2,α3,kβ1+β2线性无关B.α1,α2,α3,kβ1+β2线性相关
C.α1,α2,α3,β1+kβ2线性无关D.α1,α2,α3,β1+kβ2线性相关
(20)设α1,α2,…,αs均为n维列向量,A是m×n矩阵,则( ).
A.若α1,α2,…,αs线性相关,则Aα1,Aα2,…,Aαs必线性相关
B.若α1,α2,…,αs线性相关,则Aα1,Aα2,…,Aαs必线性无关
C.若α1,α2,…,αs线性无关,则Aα1,Aα2,…,Aαs必线性相关
D.若α1,α2,…,αs线性无关,则Aα1,Aα2,…,Aαs必线性无关
(21)n维向量组α1,α2,…,αs线性相关的充分必要条件是α1,α2,…,αs中( ).
A.有一个零向量
B.任意两个向量的分量对应成比例
C.至少有一个向量是其余向量的线性组合
D.任意一个向量都是其余向量的线性组合
(22)设n阶矩阵A=(α1,α2,…,αn),B=(β1,β2,…,βn),AB=(γ1,γ2,…,γn),记向量组(Ⅰ):α1,α2,…,αn,(Ⅱ):β1,β2,…,βn,(Ⅲ):γ1,γ2,…,γn.如果(Ⅲ)线性相关,则( ).
A.(Ⅰ)线性相关 B.(Ⅱ)线性相关
C.(Ⅰ)、(Ⅱ)都线性相关 D.(Ⅰ)、(Ⅱ)中至少有一个线性相关
(23)设向量β可由向量组α1,α2,…,αm线性表示,但不能由向量组(Ⅰ):α1,α2,…,αm-1线性表示,记向量组(Ⅱ):α1,α2,…,αm,β,则( ).(https://www.daowen.com)
A.αm不能由(Ⅰ)线性表示,也不能由(Ⅱ)线性表示
B.αm不能由(Ⅰ)线性表示,但可由(Ⅱ)线性表示
C.αm可由(Ⅰ)线性表示,也可由(Ⅱ)线性表示
D.αm可由(Ⅰ)线性表示,但不能由(Ⅱ)线性表示
(24)向量组α1,α2,…,αs,则下列说法正确的是( ).
A.如果αs不能用α1,α2,…,αs-1线性表示,则α1,α2,…,αs线性无关
B.如果α1,α2,…,αs中任一部分组都线性无关,则α1,α2,…,αs线性无关
C.如果α1,α2,…,αs线性无关,则α1+α2,α2+α3,…,αs-1+αs,αs+α1线性无关
D.如果向量组α1,α2,…,αs与向量组β1,β2,…,βs-1等价,则α1,α2,…,αs线性相关
(25)设向量组α1=(1,-1,2,4)T,α2=(0,3,1,2)T,α3=(3,0,7,14)T,α4=(1,-2,2,0)T,α5=(2,1,5,10)T,则该向量组的一个极大线性无关组为( ).
A.α1,α2,α3 B.α1,α2,α4 C.α1,α2,α5 D.α1,α2,α4,α5
(26)设m×n矩阵A的秩r(A)=m<n,则下列结论中正确的是( ).
A.A的任意m个列向量线性无关
B.A的任意m阶子行列式都不为零
C.如果矩阵B满足AB=Om×s,则n×s矩阵B=On×s
D.A经过若干次初等行变换可化为(Em︙Om×(n-m))
(27)向量组α1,α2,…,αs线性相关的充分条件是( ).
A.向量组β1,β2,…,βs-1可由α1,α2,…,αs线性表示
B.r(α1,α2,…,αs,β1,β2,…,βs-1)=r(β1,β2,…,βs-1)
C.r(α1,α2,…,αs)=r(α1,α2,…,αs,β)
D.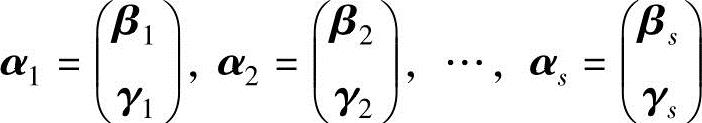 ,其中,γ1,γ2,…,γs线性相关
,其中,γ1,γ2,…,γs线性相关
(28)如果α1,α2,…,αr是向量组α1,α2,…,αr,…,αn的一个极大线性无关组,则下列结论中不正确的是( ).
A.αn可由α1,α2,…,αr线性表示B.α1可由αr+1,αr+2,…,αn线性表示
C.α1可由α1,α2,…,αr线性表示D.αn可由αr+1,αr+2,…,αn线性表示
(29)设矩阵A=(α1,α2,…,αn),其中,α1,α2,…,αn都是m维列向量,在A中去掉第i列得到的矩阵记为B,则r(A)=r(B)是αi可由B的列向量组线性表示的( ).
A.充分而非必要条件 B.必要而非充分条件
C.充分必要条件 D.既非充分又非必要条件
(30)设向量β1=α-α1,β2=α-α2,…,βs=α-αs,其中,α=α1+α2+…+αs(s>1),则( ).
A.r(α1,α2,…,αs)<r(β1,β2,…,βs)
B.r(α1,α2,…,αs)>r(β1,β2,…,βs)
C.r(α1,α2,…,αs)<r(α1,α2,…,αs,β1,β2,…,βs)
D.r(α1,α2,…,αs)=r(α1,α2,…,αs,β1,β2,…,βs)
2.解答题
(1)计算n阶行列式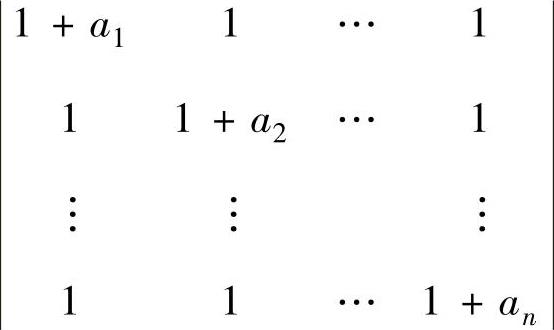 (其中,a1a2…an≠0).
(其中,a1a2…an≠0).
(2)计算n+1阶行列式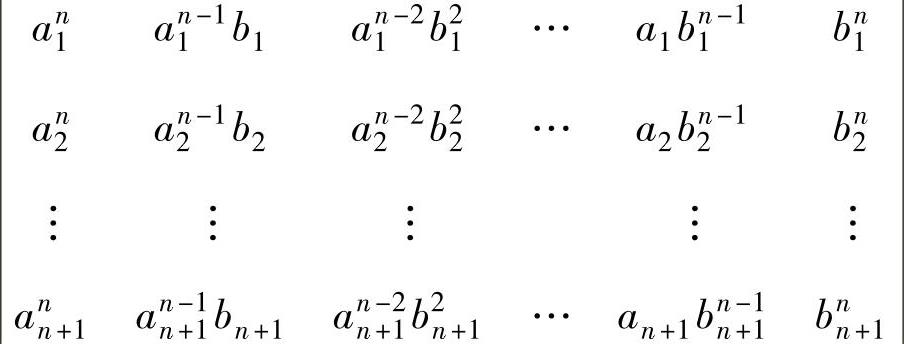 (其中,a1a2…an≠0).
(其中,a1a2…an≠0).
(3)已知三阶矩阵A的逆矩阵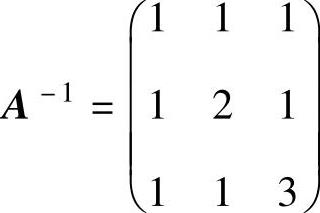 ,求A的伴随矩阵A∗的逆矩阵.
,求A的伴随矩阵A∗的逆矩阵.
(4)已知四阶矩阵A的伴随矩阵为
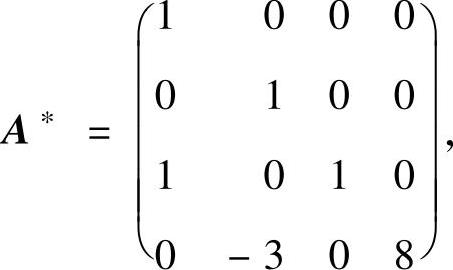
求满足ABA-1=BA-1+3E4的四阶矩阵B.
(5)设五阶矩阵
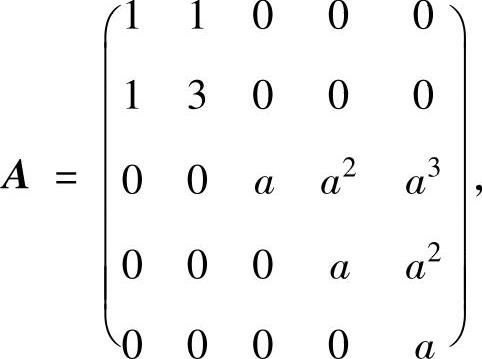
求A可逆的充分必要条件及A可逆时的A-1.
(6)设矩阵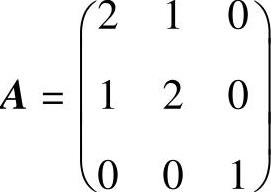 ,矩阵B满足ABA∗=2BA∗+E3,求|B|及B∗.
,矩阵B满足ABA∗=2BA∗+E3,求|B|及B∗.
(7)设三阶矩阵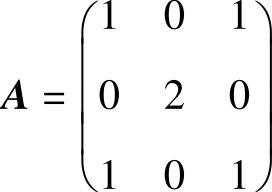 ,求An-2An-1(n是大于1的整数).
,求An-2An-1(n是大于1的整数).
(8)已知n维向量α=(a,0,…,0,a)T(a<0),求矩阵A=En-ααT为矩阵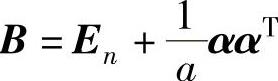 的逆矩阵时的a值.
的逆矩阵时的a值.
(9)已知A,B都是三阶矩阵,且满足
2A-1B=B-4E3.
(ⅰ)证明:矩阵A-2E3可逆;
(ⅱ)设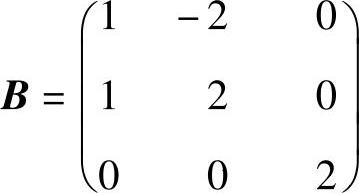 ,求A.
,求A.
(10)已知A是三阶矩阵,其行列式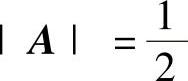 ,求行列式|(3A)-1-2A∗|.
,求行列式|(3A)-1-2A∗|.
(11)设A是4×3矩阵,且r(A)=2,而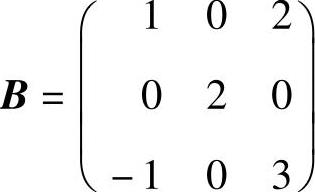 ,求r(AB).
,求r(AB).
(12)设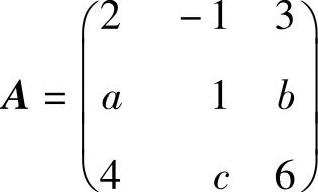 ,如果存在秩大于1的三阶矩阵B,使得AB=O3,求
,如果存在秩大于1的三阶矩阵B,使得AB=O3,求
(ⅰ)常数a,b,c;
(ⅱ)A10.
(13)已知
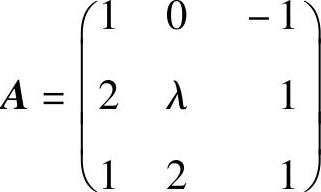
,B是秩为2的三阶矩阵,且r(AB)=1,求λ的值.
(14)按λ,μ的取值讨论矩阵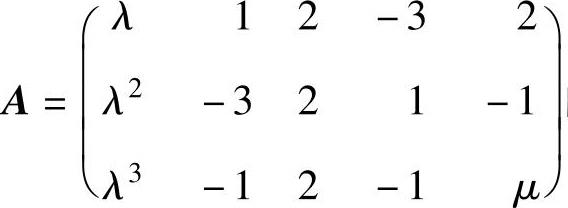 的秩r(A).
的秩r(A).
(15)设A是n阶矩阵,满足A3=En,证明n阶矩阵B=En-2A-A2可逆,并求B-1.
(16)设向量组α1=(1,2,-1)T,α2=(-1,-2,1)T,α3=(1,2,3)T,求该向量组的秩和所有极大线性无关组.
(17)已知向量组
(Ⅰ)α1=(1,0,2)T,α2=(1,1,3)T,α3=(1,-1,a+2)T,
(Ⅱ)β1=(1,2,a+3)T,β2=(2,1,a+6)T,β3=(2,1,a+4)T.问a为何值时,(Ⅰ)与(Ⅱ)等价.
(18)将向量组α1=(1,1,0,0),α2=(0,1,0,0),α3=(1,0,-1,1),α4=(0,1,1,1)单位正交化.
(19)设A是n阶矩阵,α1,α2,…,αs是n维列向量组,满足Aα1=α1,Aαi=αi-1+αi(i=2,3,…,s)且α1≠0.证明:α1,α2,…,αs线性无关.
(20)设A,B分别是m×n与n×m矩阵,其中,n≤m.若AB=Em.证明:B的列向量组线性无关.
(21)设α1=(1,3,4)T,α2=(2,5,5)T,β1=(2,3,-1)T,β2=(-3,-4,
3)T,求所有既可由α1,α2线性表示,又可由β1,β2线性表示的3维非零列向量ξ.
