随机变量的数学期望

十六 、随机变量的 数学期望

【主要内容】

1.随机变量数学期望的定义

（1）离散型情形设X是离散型随机变量，它的分布律为P（X=x_i）=p_i（i=1，2，…）.如果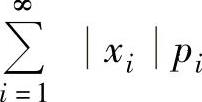

收敛，则称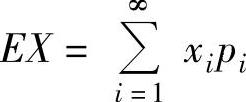为X的数学期望.

（2）连续型情形设X是连续型随机变量，它的概率密度为f（x）（-∞<x<+∞）.如果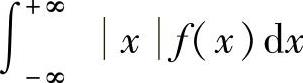

收敛，则称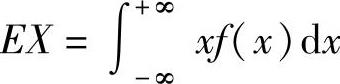为X的数学期望.

2.随机变量函数的数学期望

（1）离散型情形

设X是离散型随机变量，它的分布律为P（X=x_i）=p_i（i=1，2，…），又设g（x）是连

续函数，则X的函数g（X）的数学期望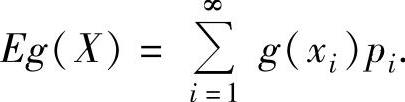

设（X，Y）是二维离散型随机变量，它的分布律为P（X=x_i，Y=y_i）=p_ij（i=1，2，…；j=1，2，…），又设h（x，y）是连续函数，则X，Y的函数h（X，Y）的数学期望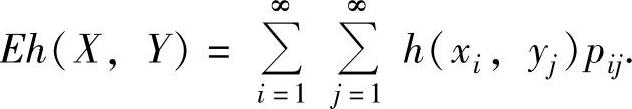

（2）连续型情形

设X是连续型随机变量，它的概率密度为f（x）（-∞<x<+∞），又设g（x）是连续函数，则X的函数g（X）的数学期望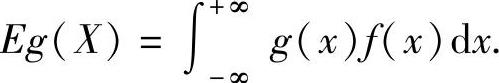

设（X，Y）是二维连续型随机变量，它的概率密度为f（x，y）（-∞<x<+∞，-∞<y<+∞），又设h（x，y）是连续函数，则X，Y的函数h（X，Y）的数学期望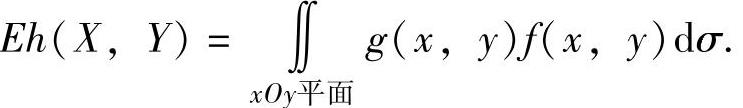

3.数学期望的性质

设X，Y是随机变量，c，c₁，c₂是常数，则

（1）Ec=c；

（2）E（c₁X+c₂Y）=c₁EX+c₂EY；

（3）当X与Y相互独立时，E（XY）=EX·EY.

4.常用随机变量的数学期望

设X服从0-1分布，则EX=p；

设X～B（n，p），则EX=np；

设X～π（λ），则EX=λ；

设X～U（a，b），则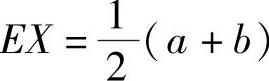；(https://www.daowen.com)

设X～E（λ），则；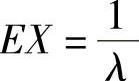

设X～N（μ，σ²），则EX=μ.

【典型例题】

例7.16.1 将3只球随机地放入编号为1，2，3，4的四个盒中，以X表示有球盒的最大号码，求EX.

精解 先计算X的分布律.

X全部可能取的值为1，2，3，4，对应的概率为

P（X=1）=P{3只球全部放入1号盒，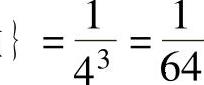

P（X=2）=P{3只球中至少有1只放入2号盒，而其余的全放入1号盒}，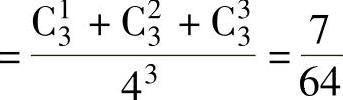

P（X=3）=P{3只球中至少有1只放入3号盒，而其余的全放入1号盒或2号盒}，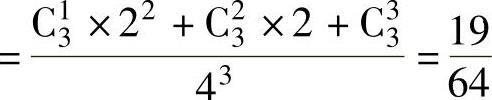

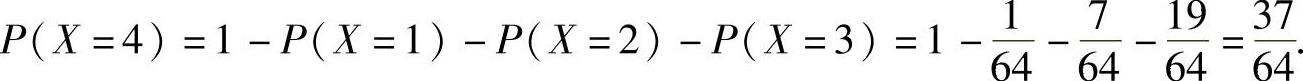
所以由数学期望的定义得

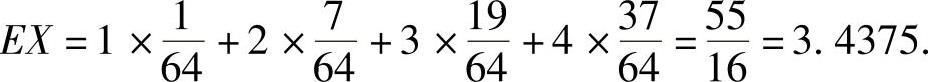
例7.16.2 某车站每天8：00～9：00，9：00～10：00都恰有一辆客车到站，但到站时刻是随机的，且两个时间区间里到站时刻相互独立，具体规律如下：

今有一乘客于8：20到车站，求他候车时间X（单位：min）的数学期望.

精解 先写出X的分布律：

X可能取的值为10，30，50，70，90，为了计算对应的概率，记

A₁={第一班车8：10到站}， A₂={第一班车8：30到站}，

A₃={第一班车8：50到站}， B₁={第二班车9：10到站}，

B₂={第二班车9：30到站}， B₃={第二班车9：50到站}，则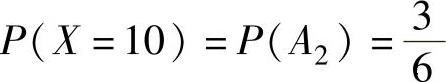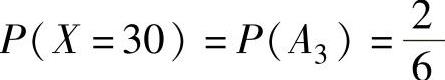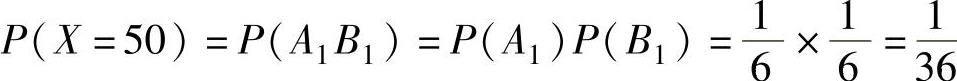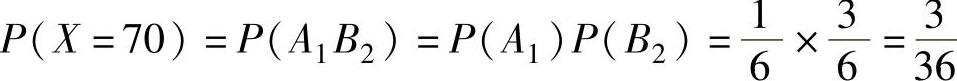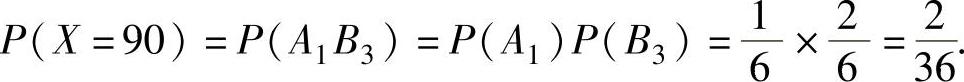，，，，于是，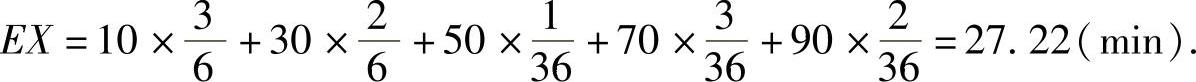

例7.16.3 设连续型随机变量的分布函数为

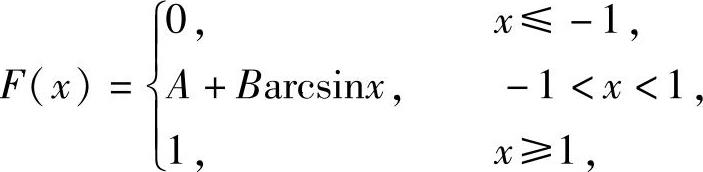
求EX.

精解 先确定常数A，B.

由于F（x）是连续型随机变量的分布函数，所以它是连续函数，特别在点x=-1，1处连续，于是有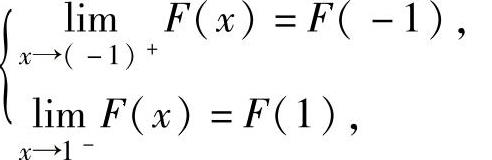即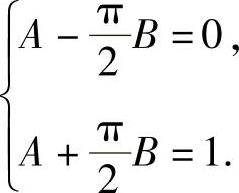

解此方程组得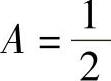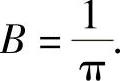，因此

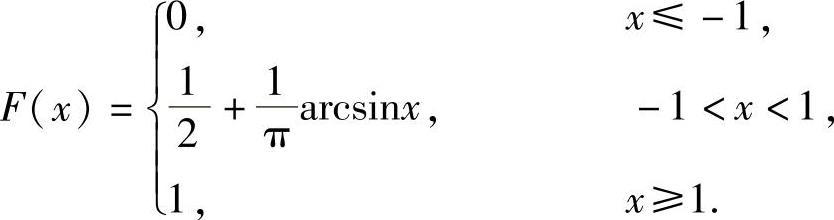
由此得到X的概率密度

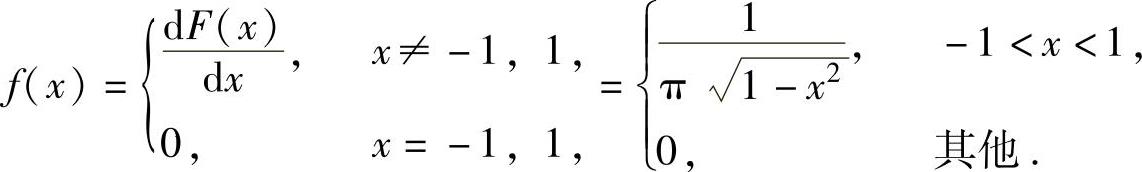
于是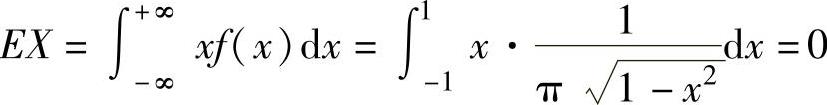，（对称区间上奇函数的积分为零）.

例7.16.4 设随机变量X与Y分别服从参数均为1的指数分布与泊松分布，求概率P（X²+Y²≤E（X+Y））.

精解 由于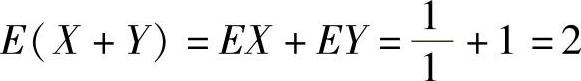，所以

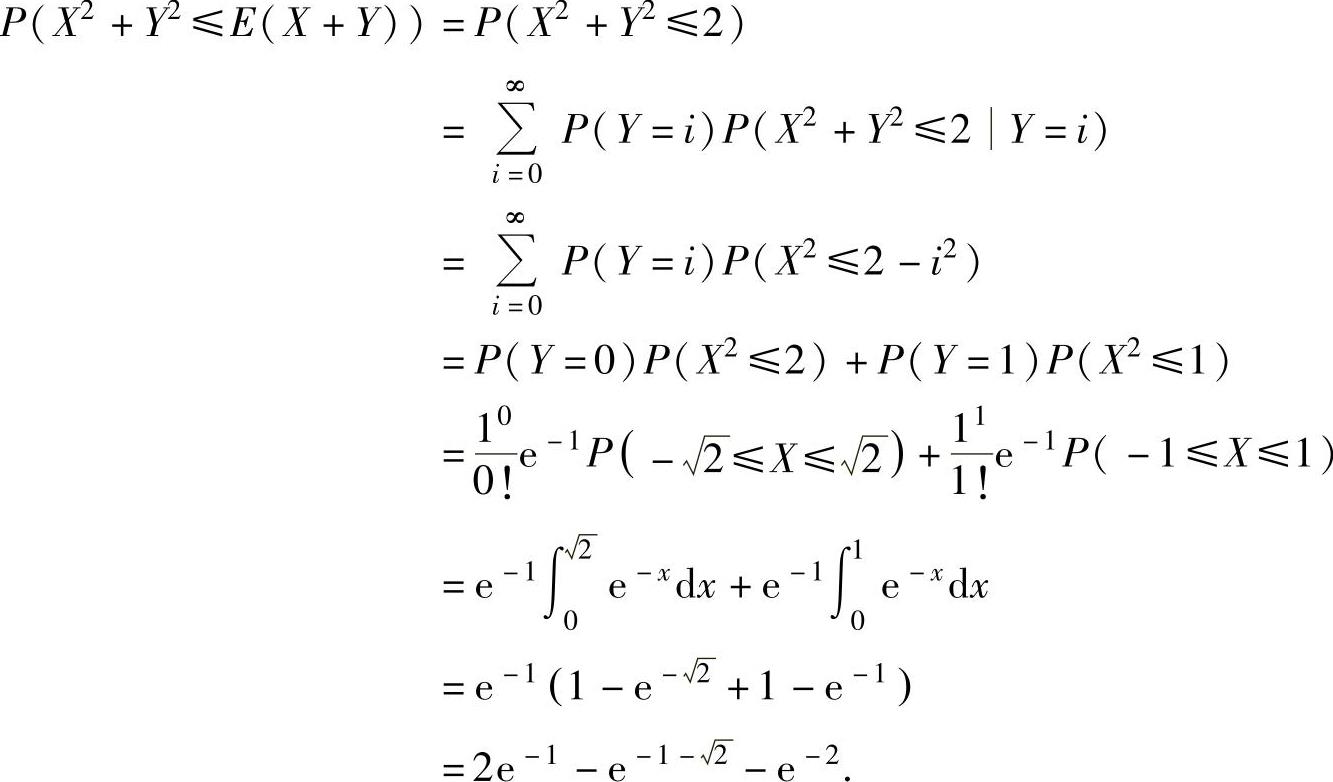
例7.16.5 设随机变量X与Y相互独立，且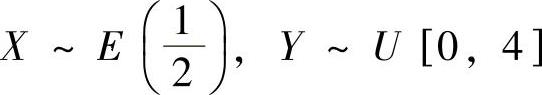，求

E（min{X，Y}）和E（X+XY+2）.

精解 由题设知X与Y的概率密度分别为

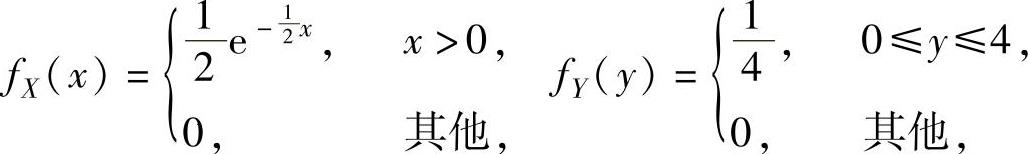
所以，由X与Y相互独立知二维随机变量（X，Y）的概率密度为，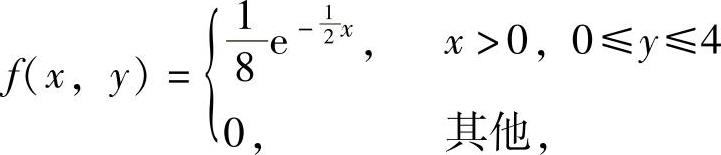

即它在D={（x，y）x>0，0≤y≤4}（如图7.16.5阴影部分所示）上取值为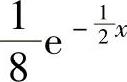，在xOy

平面的其他部分取值为零.

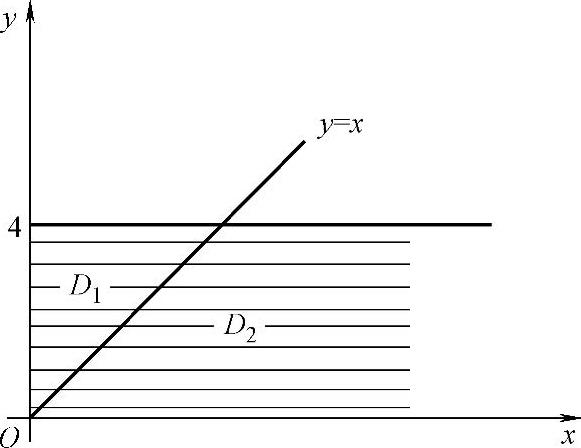
图 7.16.5

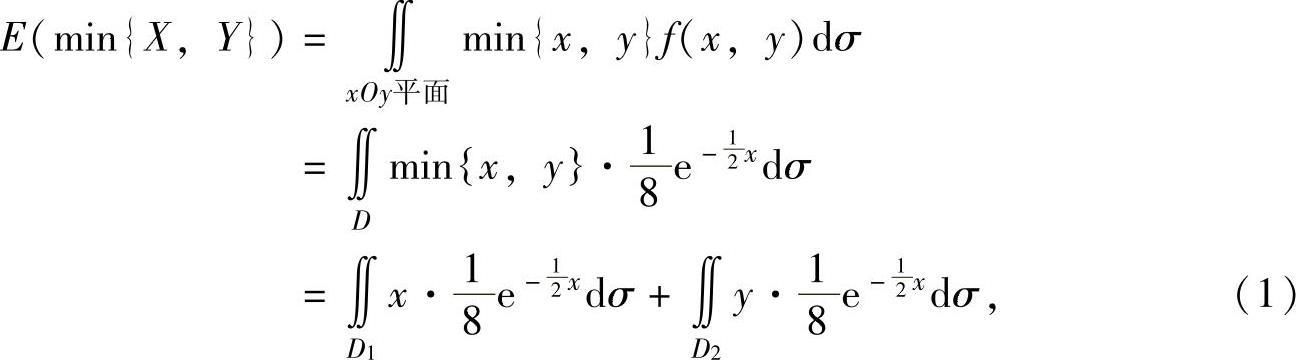
其中，D₁与D₂是D被直线y=x划分成的两部分，如图7.16.5所示，并且

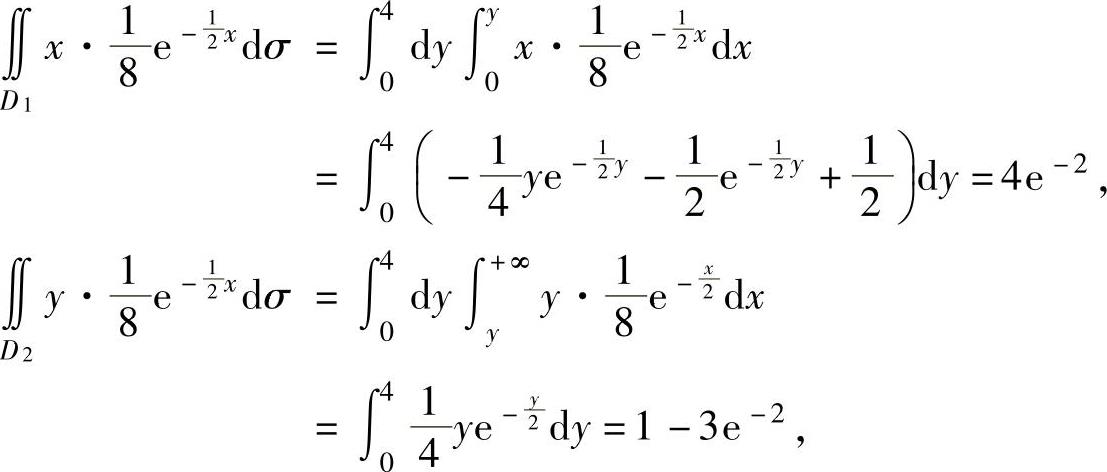
将它们代入式（1）得

E（min{X，Y}）=4e^-2+（1-3e^-2）=1+e^-2.下面计算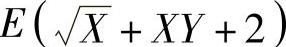

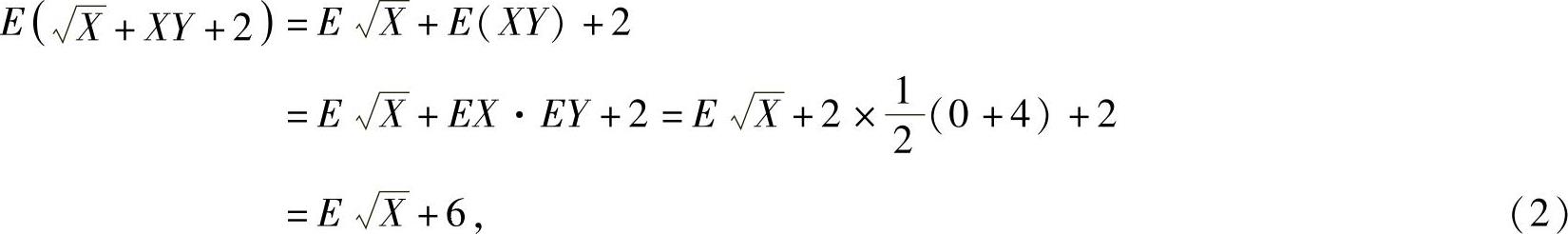
其中，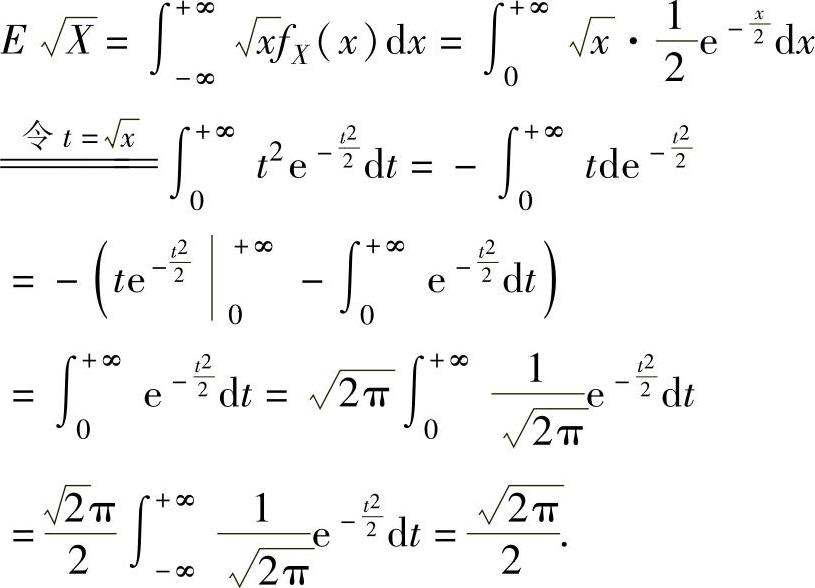

将它代入式（2）得