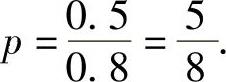随机事件的独立性
【主要内容】
1.随机事件独立性的定义
(1)两个事件独立性的定义
设A,B是事件,如果P(AB)=P(A)P(B),则称A与B相互独立,简称独立;否则称A与B不独立.
(2)三个事件独立的定义
设A,B,C是事件,如果A,B,C中任意两个都是独立的,则称A,B,C两两独立;如果A,B,C两两独立,且满足P(ABC)=P(A)P(B)P(C),则称A,B,C相互独立,或简称独立.
2.随机事件独立的性质
设A,B,C都是事件,则
(1)当P(A)>0时,A与B独立的充分必要条件是P(B|A)=P(B).
(2)四组事件:A与B,A与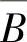 ,
,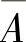 与
与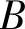 以及A与B中有一组的两个事件独立时,其余
以及A与B中有一组的两个事件独立时,其余
各组的两个事件必独立.
(3)A,B,C独立时必两两独立.
(4)当A,B,C独立时,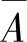 ,
,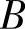 ,C;
,C;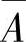 ,
,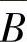 ,C;…;
,C;…;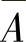 ,
,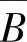 ,
,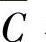 各组的三个事件也必独立.
各组的三个事件也必独立.
【典型例题】
例7.3.1 (单项选择题)将一枚硬币独立地掷两次,记事件
A1={掷第一次时,出现正面},
A2={掷第二次时,出现正面},
A3={正、反面各出现一次},
A4={正面出现两次},则( ).
A.A1,A2,A3相互独立 B.A2,A3,A4相互独立
C.A1,A2,A3两两独立 D.A2,A3,A4两两独立
精解 首先注意,如果选项A正确,则选项C必正确,这对单项选择题来说是不可能的,所以排除选项A,同样排除B.
由于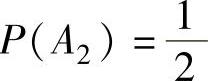 ,
,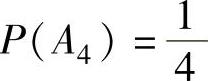 ,
,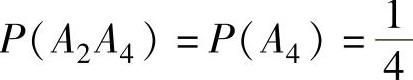 ,
,
所以P(A2A4)≠P(A2)P(A4),由此可知A2与A4不独立,即A2,A3,A4不两两独立,选项D应排除.(https://www.daowen.com)
因此本题选C.
例7.3.2 (单项选择题)设A,B是事件,它们满足0<P(A)<1,0<P(B)<1,且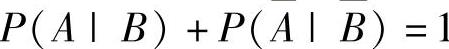 ,则( ).
,则( ).
A.A与B互不相容 B.A与B对立
C.A与B不独立 D.A与B独立
精解 由题设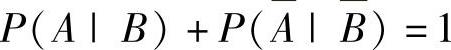 得
得
P(A|B)=1-P(A|B)=P(A|B).由此可知,B发生与否不影响A发生的概率.所以A与B独立.
因此本题选D.
例7.3.3 设独立事件A,B都不发生的概率为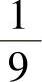 ,且A发生而B不发生的概率与B发
,且A发生而B不发生的概率与B发
生而A不发生的概率相等,求P(A).
精解 由题设知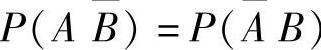 ,
,
即P(A)-P(AB)=P(B)-P(AB),所以P(A)=P(B).
此外,由A与B独立知 与
与 独立,所以由
独立,所以由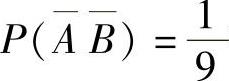 得
得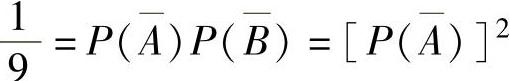 ,
,
即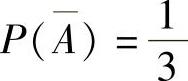 ,从而
,从而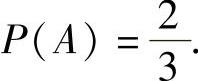
例7.3.4 甲、乙两人独立地对某一目标各射击一次,命中率分别为0.6和0.5,现已知目标被击中,求它是被乙击中的概率p.
精解 引入事件:
A={甲击中目标}, B={乙击中目标}, C={目标被击中}.
由于C=A∪B,所以概率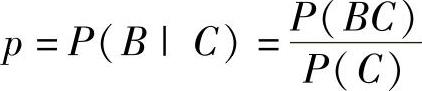 ,(1)
,(1)
其中 P(BC)=P(B(A∪B))
=P(AB∪B)=P(B)(由于AB⊂B,所以AB∪B=B)
=0.5,
P(C)=P(A∪B)=P(A)+P(B)-P(AB)
=P(A)+P(B)-P(A)P(B)(由于A与B独立)
=0.6+0.5-0.6×0.5=0.8.
将它们代入式(1)得