级数收敛性的概念与收敛级数的性质
【主要内容】
1.级数收敛性的概念
设数列{un},则称记号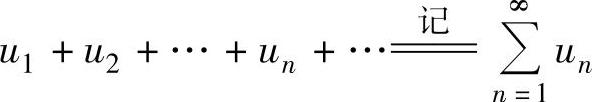 为无穷级数,简称级数.记
为无穷级数,简称级数.记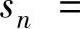
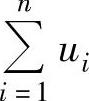 ,则称{sn}为级数
,则称{sn}为级数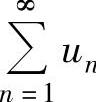 的部分和数列.如果{sn}收敛于s,则称级数
的部分和数列.如果{sn}收敛于s,则称级数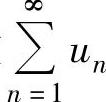 收敛,且称s
收敛,且称s
为该级数的和,记为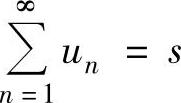 ;如果{sn}发散,则称级数
;如果{sn}发散,则称级数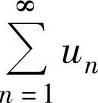 发散.
发散.
2.收敛级数的基本性质
(1)如果级数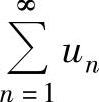 和
和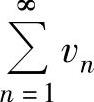 分别收敛于u与v,则级数
分别收敛于u与v,则级数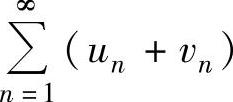 和
和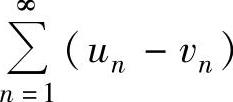 都收
都收
敛,它们的和分别为u+v和u-v.
(2)如果级数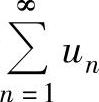 收敛,k为常数,则级数
收敛,k为常数,则级数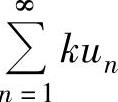 收敛,且当
收敛,且当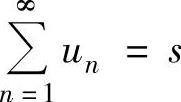 时,
时,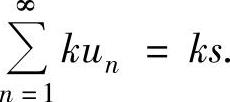
(3)如果级数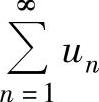 收敛,则在它的前面任意添加有限项、去掉或改变它开头的有限项而成的级数仍收敛.
收敛,则在它的前面任意添加有限项、去掉或改变它开头的有限项而成的级数仍收敛.
(4)如果级数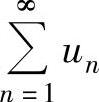 收敛,则对它的项任意加括号后所得级数仍收敛,且其和不变.
收敛,则对它的项任意加括号后所得级数仍收敛,且其和不变.
(5)如果级数收敛,则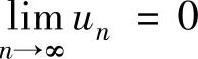 (级数收敛的必要条件).
(级数收敛的必要条件).
3.常用级数收敛性
(1)级数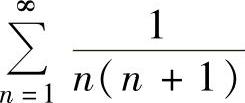 收敛,且其和为1.
收敛,且其和为1.
(2)等比级数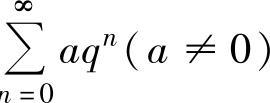 :当0<q<1时,
:当0<q<1时,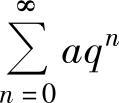 收敛,且其和为
收敛,且其和为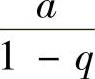 ;当q≥
;当q≥
1时,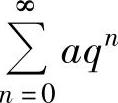 发散.
发散.
(3)p级数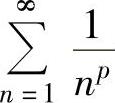 :当p>1时,
:当p>1时,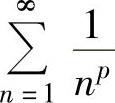 收敛;当p≤1时,
收敛;当p≤1时,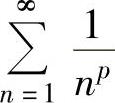 发散.
发散.
(4)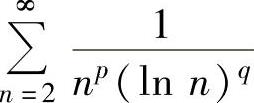 :当p>1或p=1而q>1时,
:当p>1或p=1而q>1时,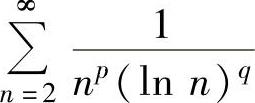 收敛;当p<1或p=1
收敛;当p<1或p=1
而q≤1时,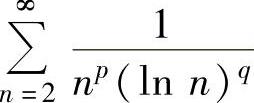 发散.
发散.
【典型例题】
例4.8.1(单项选择题) 设有命题
① 如果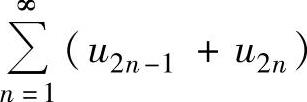 收敛,则
收敛,则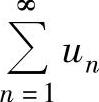 收敛.
收敛.
② 如果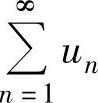 收敛,则
收敛,则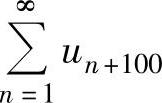 收敛.
收敛.
③ 如果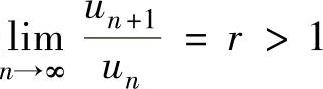 ,则
,则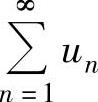 发散.
发散.
④ 如果 收敛,则
收敛,则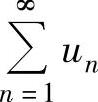 和
和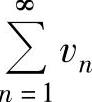 都收敛.则以上命题中正确的是( ).
都收敛.则以上命题中正确的是( ).
A.①② B.②③ C.③④ D.①④(https://www.daowen.com)
精解 由收敛级数基本性质知,当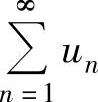 收敛时,
收敛时,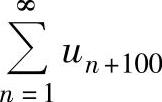 收敛,所以命题②正确.
收敛,所以命题②正确.
在假定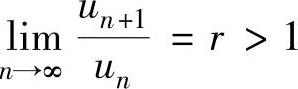 成立的情况下,必存在正整数N,当n≥N时有
成立的情况下,必存在正整数N,当n≥N时有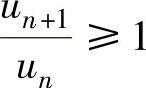 ,于是由
,于是由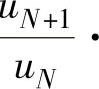
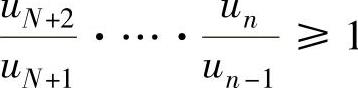 ,即
,即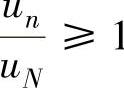 知
知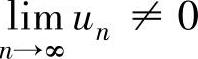 ,
,
所以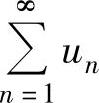 发散.所以命题③正确.
发散.所以命题③正确.
因此本题选B.
例4.8.2(单项选择题) 设由收敛级数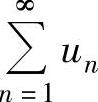 构造以下级数
构造以下级数
①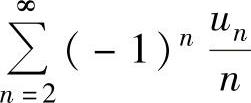 ,②
,②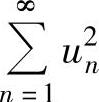 ,
,
③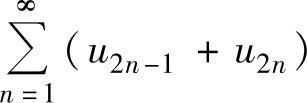 ,④
,④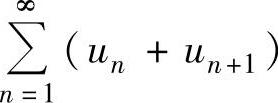 ,
,
则上面四个级数中必收敛的是( ).
A.①② B.②③ C.③④ D.①④
精解 由于③是对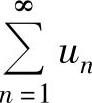 两项加括号而成的级数,所以由收敛级数的基本性质知,③必收敛.
两项加括号而成的级数,所以由收敛级数的基本性质知,③必收敛.
由于④是两个收敛级数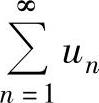 与
与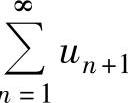 相加而成的级数,所以由收敛级数的基本性质
相加而成的级数,所以由收敛级数的基本性质
知,④必收敛.
因此本题选C.
注 (ⅰ)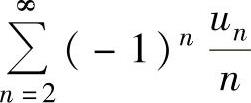 未必收敛.例如
未必收敛.例如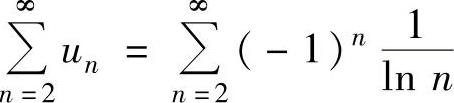 收敛,但
收敛,但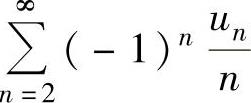
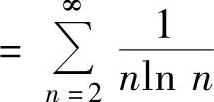 发散.
发散.
(ⅱ)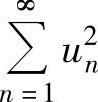 也未必收敛,例如
也未必收敛,例如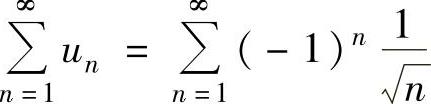 收敛,但
收敛,但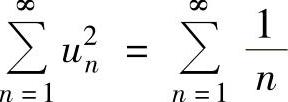 发散.
发散.
例4.8.3(单项选择题) 如果级数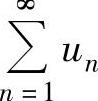 ,
,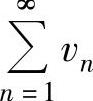 都发散,则( ).
都发散,则( ).
A.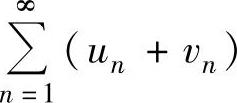 必发散B.
必发散B.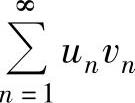 必发散
必发散
C.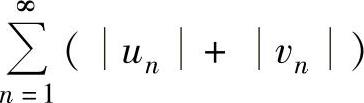 必发散D.
必发散D.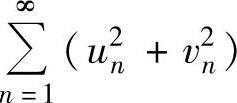 必发散
必发散
精解 选项A,B,D是不正确的.例如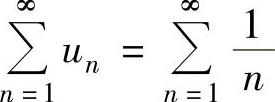 ,
,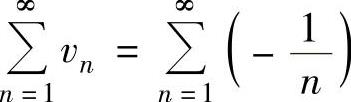 都是发散级数,
都是发散级数,
但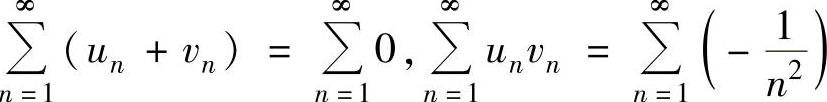 ,
,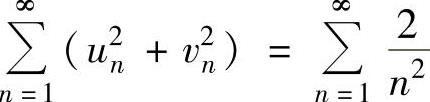 都是收敛的.
都是收敛的.
因此本题选C.
例4.8.4 求级数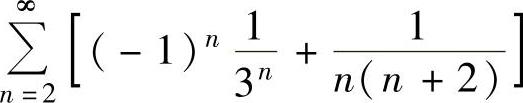 的和.
的和.
精解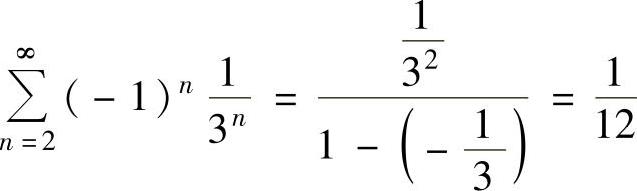 ,
,
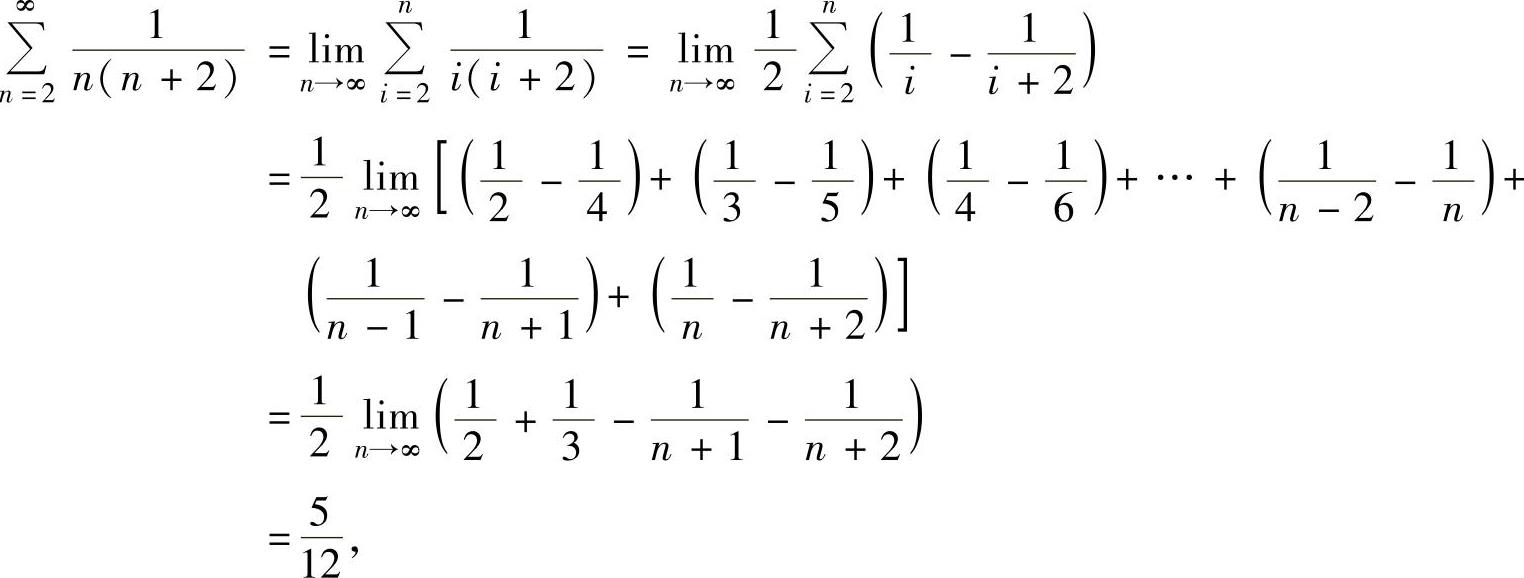
所以,