五、函数的间断点

五 、函数的间断点

【主要内容】

1.函数间断点的定义

如果函数f（x）在点x₀处不连续（即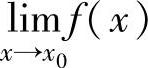不存在，或f（x）在点x₀处无定义，或虽然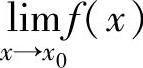与f（x₀）都存在，但它们不相等），则称x₀是f（x）的间断点.

2.函数间断点分类

（1）第一类间断点

设x₀是f（x）的间断点，如果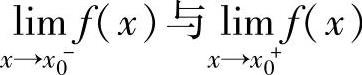都存在，则称x₀是f（x）的第一类间断

点.特别地，当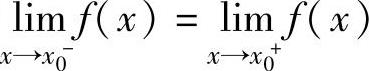（即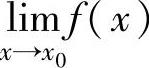存在）时，称x₀是f（x）的可去间断点；当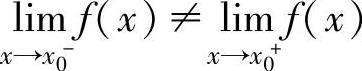时，称x₀是f（x）的跳跃间断点.

（2）第二类间断点

设x₀是f（x）的间断点，但不是第一类间断点，则称x₀是f（x）的第二类间断点，特别

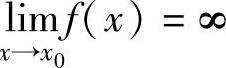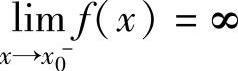地，当，或，或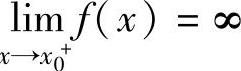时，称x₀是f（x）的无穷间断点，它

是常见的第二类间断点.

【典型例题】

例1.5.1 设函数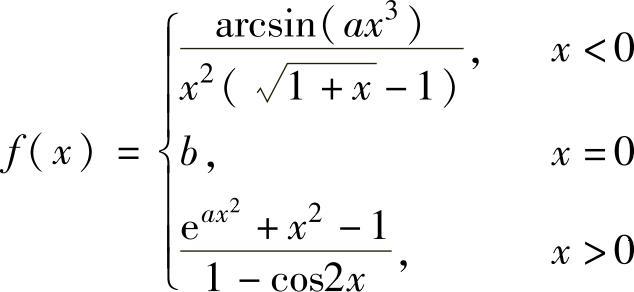，，问常数a，b为何值时，x=0是，

f（x）的可去间断点.

精解 根据可去间断点的定义有

其中，，，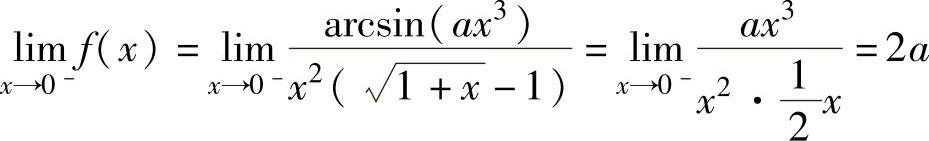

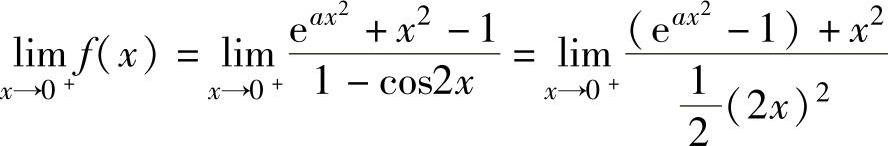
f（0）=b.

将它们代入式（1）得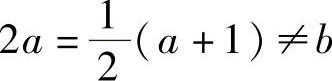，即，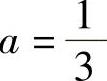

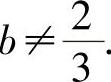
例1.5.2 设函数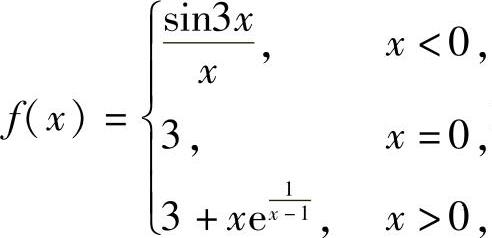求f（x）的间断点（需指明类型）与连续区间(https://www.daowen.com)

（即使f（x）连续的区间）.

精解 当x<0时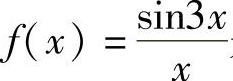，是连续的；当x>0时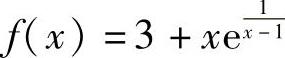，除点x=1外，处

处连续，所以f（x）的可能间断点为x=0，1.

由于，，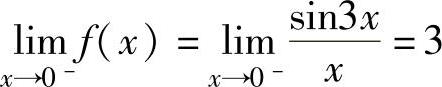

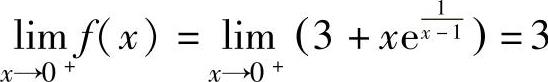且f（0）=3，即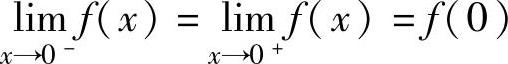，所以x=0不是函数f（x）的间断点，而是连续

点.

由于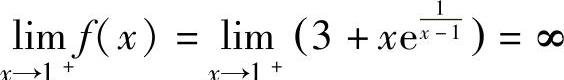，所以，x=1是f（x）的第二类间断点，且是无穷

间断点.

综上所述，f（x）有唯一的间断点x=1（第二类间断点，且是无穷间断点），连续区间为（-∞，1）和（1，+∞）.

例1.5.3 求函数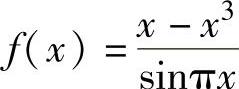的可去间断点的个数.

精解 由于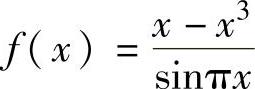是初等函数，它的间断点为分母为零的点，即x=0，±1，

±2，….

由于，，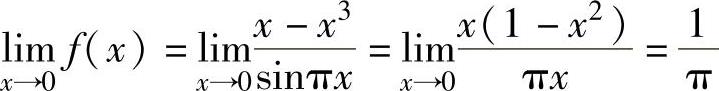

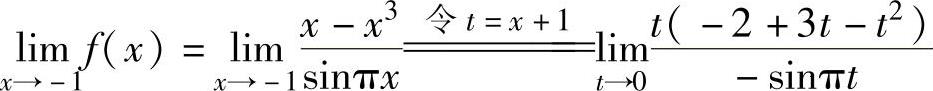
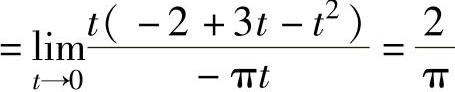且由f（x）是偶函数可得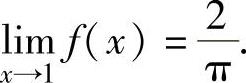

此外，对k=±2，±3，…，有，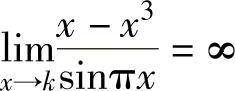

所以，f（x）仅有3个可去间断点，它们为x=0，-1，1.

例1.5.4 求函数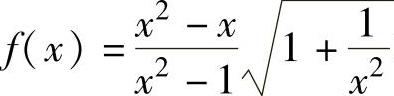的无穷间断点.

精解 f（x）有间断点x=-1，0，1.

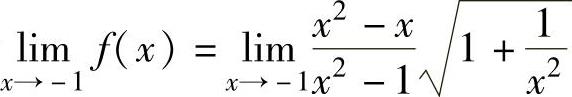
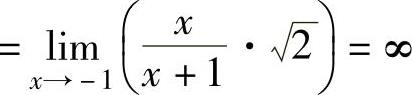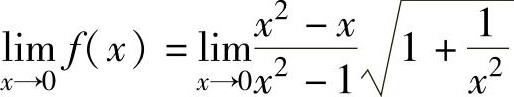
由于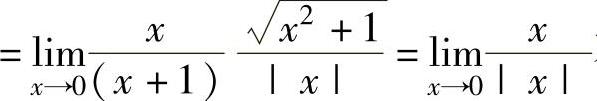，不存在，但不为无穷大，，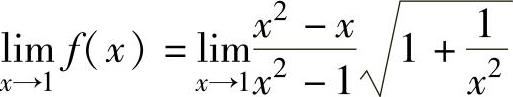

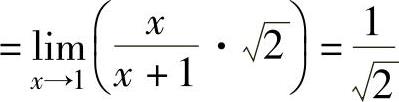所以，f（x）只有一个无穷间断点，即x=-1.