二维离散型随机变量及其分布律
【主要内容】
1.二维随机变量的定义
设E是随机试验,则称由定义在E的样本空间Ω上的随机变量X与Y构成的有序对(X,Y)为二维随机变量.
2.二维离散型随机变量及其分布律
设(X,Y)是二维随机变量,如果(X,Y)全部可能取的值是有限多个对或可列无限多个对时,则称(X,Y)为离散型随机变量.
设(X,Y)是二维离散型随机变量,它全部可能取的值为(xi,yj)(i=1,2,…,m;j=1,2,…,n或者i,j=1,2,…),且取这些值对应的概率为pij(i=1,2,…,m;j=1,2,…,n或者i,j=1,2,…),则称

或

(简记为P(X=xi,Y=yj)=pij,i=1,2,…,m,j=1,2,…,n)(简记为P(X=xi,Y=yj)=pij,i,j=1,2,…)
为(X,Y)的分布律,其中pij有以下性质:
(1)每个pij≥0;
(2)ΣiΣjpij=1.
3.二维离散型随机变量的边缘分布律设(X,Y)是二维离散型随机变量,且分布律为P(X=xi,Y=yj)=pij(i=1,2,…,
m;j=1,2,…,n或者i,j=1,2,…),则分别称X,Y的分布律
P(X=xi)=pi·(i=1,2,…,m或i=1,2,…),
P(Y=yj)=p·j(j=1,2,…,n或j=1,2,…)
为(X,Y)的关于X和关于Y的边缘分布律,其中
pi·=Σjpij(i=1,2,…,m或i=1,2,…),
p·j=Σipij(j=1,2,…,n或j=1,2,…).
4.二维离散型随机变量的条件分布律设(X,Y)是二维离散型随机变量,它的分布律及边缘分布律分别为P(X=xi,Y=yj)=pij(i=1,2,…,m;j=1,2,…,n或者i,j=1,2,…),P(X=xi)=pi·(i=1,2,…,m或者i=1,2,…),P(Y=yj)=p·j(j=1,2,…,n或者j=1,2,…),
可以用表表示为
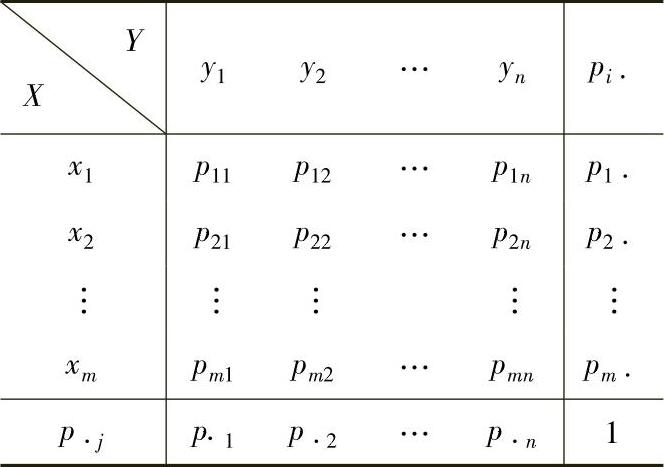
或者

则当p·j≠0时,称
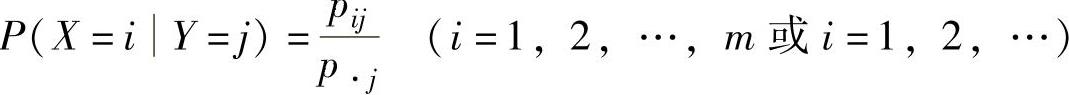
为在条件Y=yj下X的条件分布律;当pi·≠0时,称
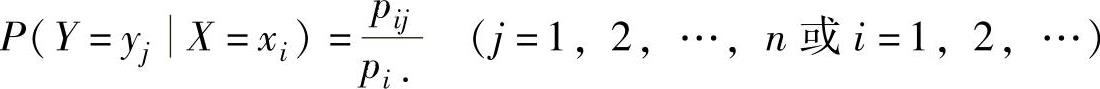
为在条件X=xi下Y的条件分布律.
【典型例题】
例7.9.1 设随机变量T~U[-2,2],记
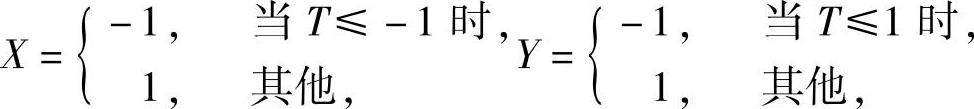
求二维随机变量(X,Y)的分布律.
精解 X,Y都只取-1与1两个值,所以(X,Y)全部可能取的值有四对:(-1,-1),(-1,1),(1,-1)以及(1,1),并且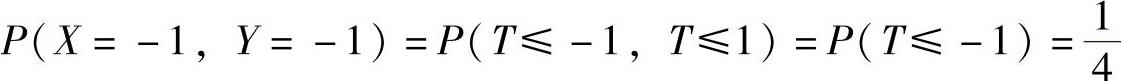 ,P(X=-1,Y=1)=P(T≤-1,T>1)=P(Φ)=0,
,P(X=-1,Y=1)=P(T≤-1,T>1)=P(Φ)=0,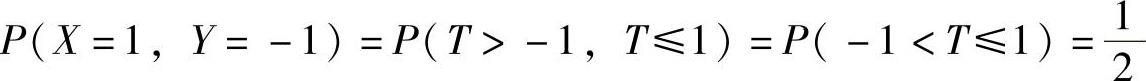 ,
,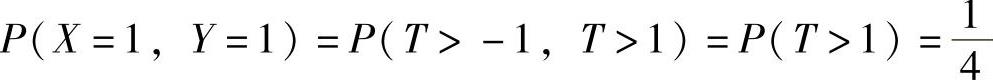 ,
,
所以(X,Y)的分布律为
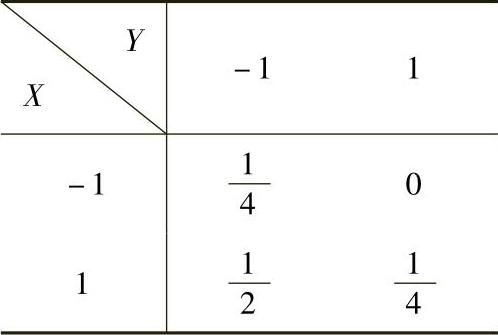
例7.9.2 将两封信等可能地投入编号为Ⅰ,Ⅱ,Ⅲ的三个邮箱中,记X,Y分别为投入Ⅰ号与Ⅱ号邮箱中信的数目,求二维随机变量(X,Y)的分布律与关于X的边缘分布律.
精解 X与Y可能取的值都为0,1,2,所以(X,Y)全部可能取的值为(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),并且
 (https://www.daowen.com)
(https://www.daowen.com)
P(X=2,Y=1)=P{X=2,Y=2}=P(Φ)=0.
因此,(X,Y)分布律列表如下:
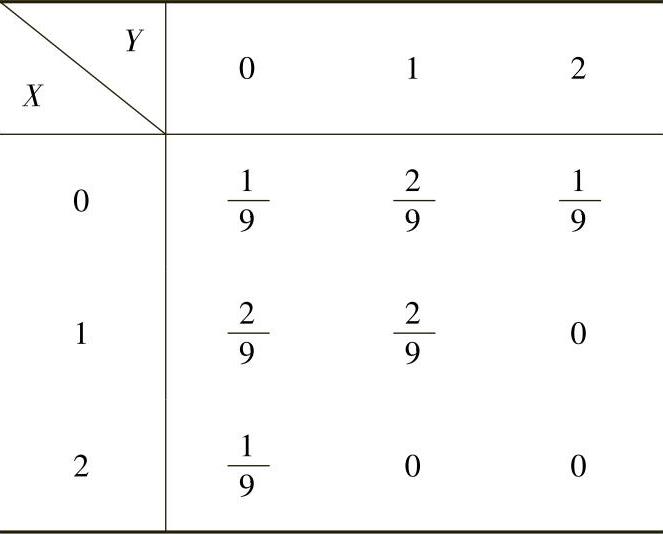
由上表可得关于X的边缘分布律为
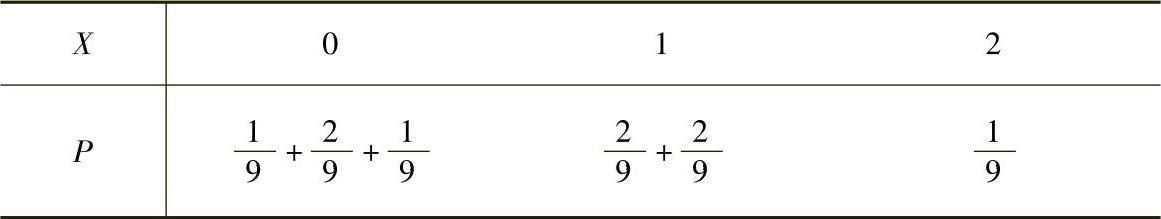
即

例7.9.3 设二维随机变量(X,Y)的分布律为
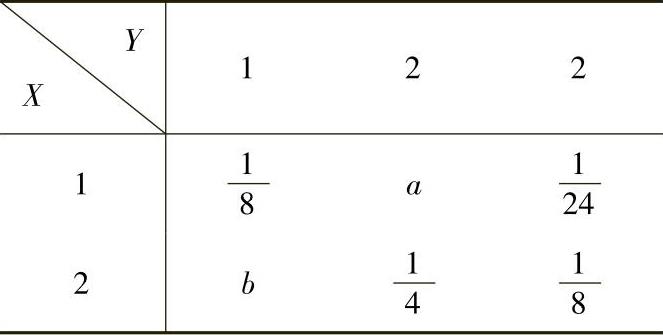
且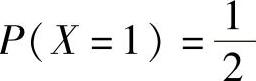 ,求:
,求:
(1)常数a,b的值;
(2)求关于Y的边缘分布律;
(3)在Y=2的条件下,X的条件分布律.
精解 (1)利用分布律的性质与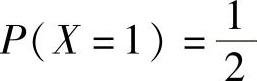 计算a,b的值.
计算a,b的值.
由分布律的性质知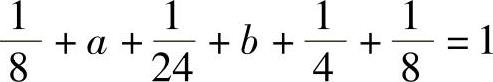 ,即
,即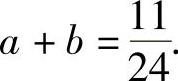 (1)
(1)
此外,由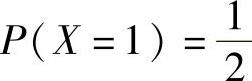 得
得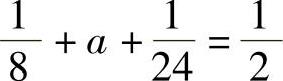 ,即
,即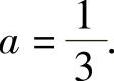
将它代入式(1)得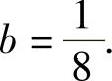
(2)由(1)的计算知(X,Y)的分布律为
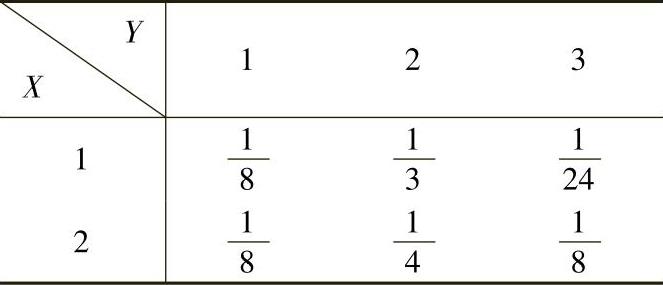
于是,(X,Y)关于Y的边缘分布律为
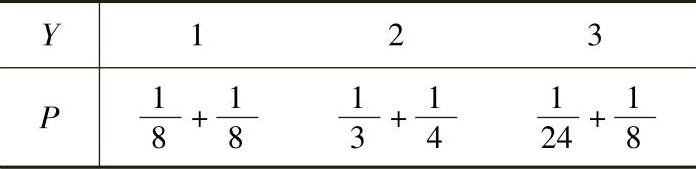
即
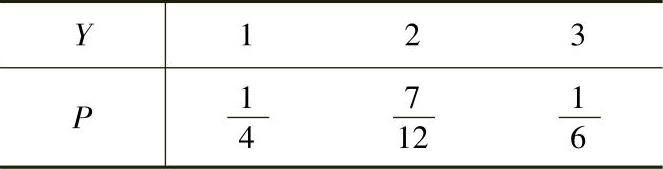
(3)在Y=2的条件下,X的条件概率分布律为
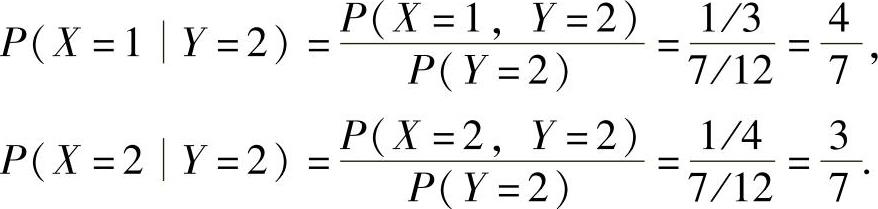
例7.9.4 设随机变量X,Y的分布律如下:
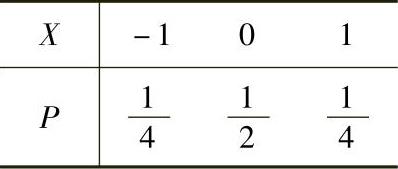
,
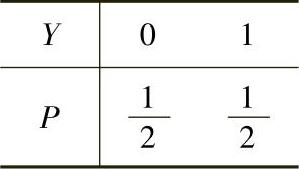
且P(XY=0)=1,求二维随机变量(X,Y)的分布律及在条件Y=0下X的分布律.
精解 先计算(X,Y)的分布律,设其为
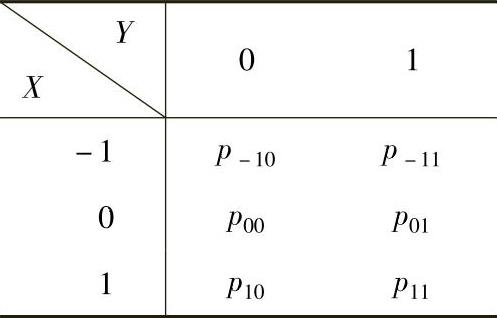
由P(XY=0)=1得
p-10+p00+p01+p10=1,
于是由分布律的性质知p-11+p11=0,即p-11=p11=0.
由表可知,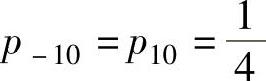 ,
,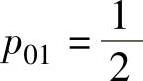 ,并由
,并由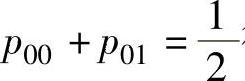 得p00=0.因此(X,Y)的分布律
得p00=0.因此(X,Y)的分布律
及边缘分布律为
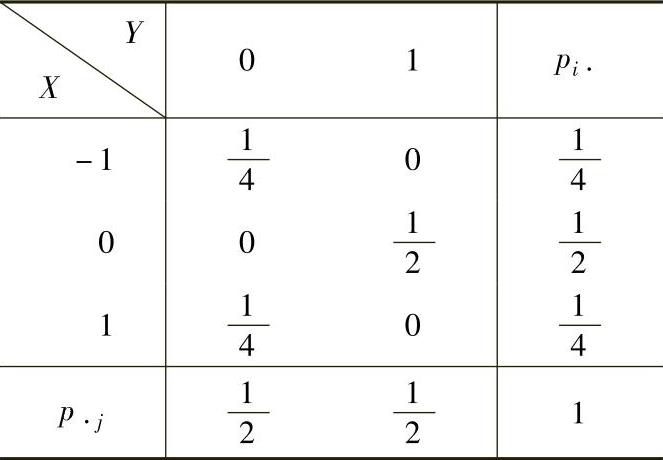
下面计算条件分布律P(X=iY=0)(i=-1,0,1):