练习题二
1.单项选择题
(1)设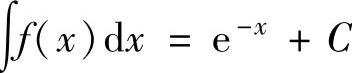 ,则不定积分
,则不定积分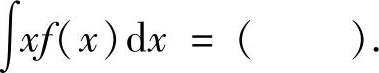
A.e-x(x+1)+C B.-e-x(x-1)+C
C.e-x(x-1)+C D.-e-x(x+1)+C
(2)设f(x)的一个原函数为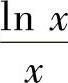 ,则∫f′(x)dx=( ).
,则∫f′(x)dx=( ).
A.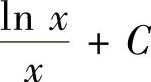 B.
B.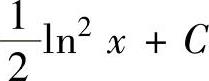
C.ln|lnx|+CD.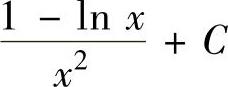
(3)设f(x)是连续函数,F(x)是f(x)的原函数,则( ).
A.当f(x)是奇函数时,F(x)必为偶函数
B.当f(x)是偶函数时,F(x)必为奇函数
C.当f(x)是周期函数时,F(x)必为周期函数
D.当f(x)是单调增加函数时,F(x)必为单调增加函数
(4)设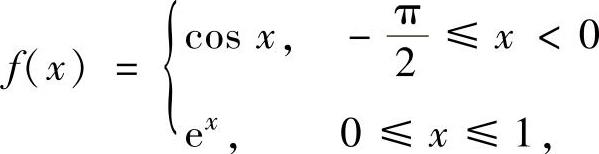 ,则下列函数中为f(x)原函数的是( ).
,则下列函数中为f(x)原函数的是( ).
A.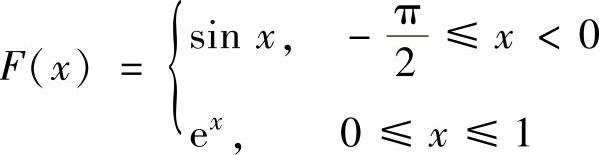 ,B.
,B.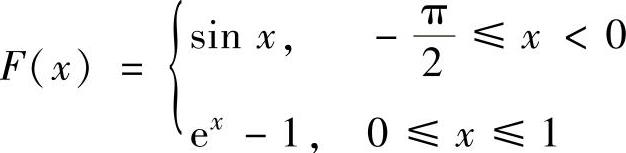 ,
,
C.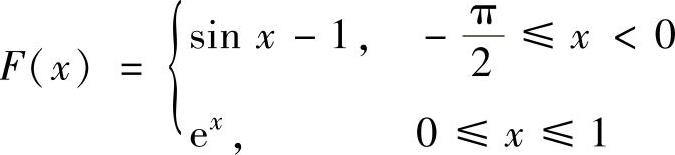 ,D.
,D.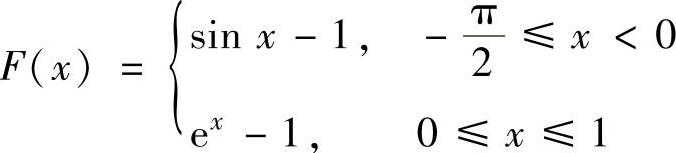 ,
,
(5)设f(x)与g(x)都是[0,1]上的连续函数,且f(x)≤g(x),则对任何c∈(0,1)有( ).
A.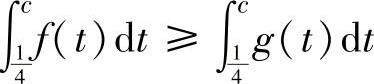 B.
B.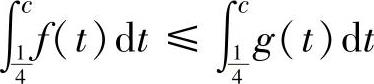
C.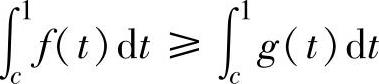 D.
D.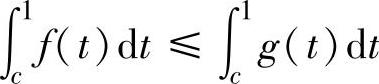
(6)设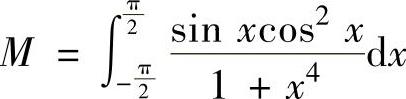 ,
,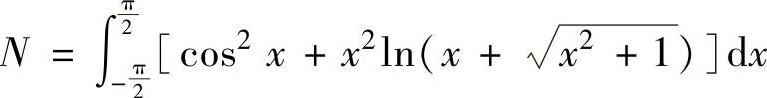 ,
,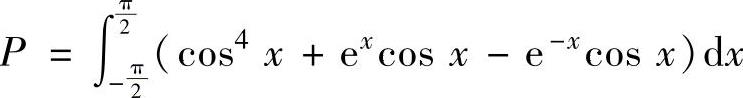 ,则有( ).
,则有( ).
A.M<N<P B.M<P<N
C.P<M<N D.N<M<P
(7)设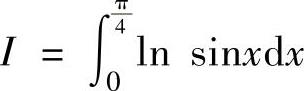 ,
,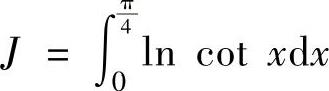 ,K
,K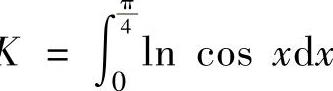 ,则I,J,K的大小关系是( ).
,则I,J,K的大小关系是( ).
A.I≤J≤K B.I≤K≤J
C.J≤I≤K D.K≤J≤I
(8)设在[a,b]上,函数f(x)有二阶导数,且f(x)>0,f′(x)<0,f″(x)>0,记S1=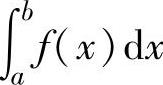 ,S2=f(b)(b-a),
,S2=f(b)(b-a),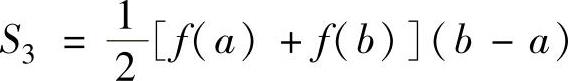 ,则有( ).
,则有( ).
A.S1<S2<S3 B.S2<S1<S3
C.S3<S1<S2 D.S2<S3<S1
(9)设函数f(x)连续,则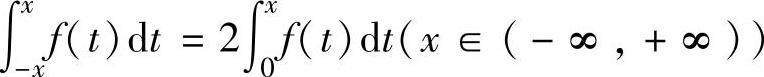 的( ).成立是f(x)为偶函数
的( ).成立是f(x)为偶函数
A.充分而非必要条件 B.必要而非充分条件
C.充分必要条件 D.既非必要又非充分条件
(10)设f(x)是以l(l>0)为周期的连续函数,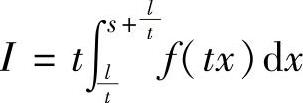 (其中,t>0),则( ).
(其中,t>0),则( ).
A.I依赖s而不依赖t,l
B.I依赖t而不依赖s,l
C.I依赖s和t而不依赖l
D.I不依赖s,t及l
(11)当x→0时,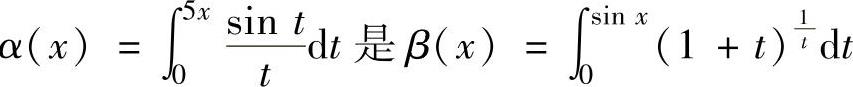 的( ).
的( ).
A.低阶无穷小 B.高阶无穷小
C.同阶但不是等价无穷小 D.等价无穷小
(12)设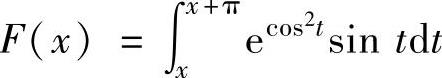 ,则F(x)是( ).
,则F(x)是( ).
A.周期为π的周期函数 .取正值的函数
C.周期为2π的周期函数 D.取负值的函数
(13)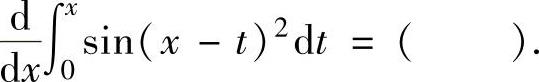
A.sint2 B.sinx2 C.2xsinx2 D.2tsint2
(14)设函数f(x)在[a,b]上连续,且f(x)>0,又设函数
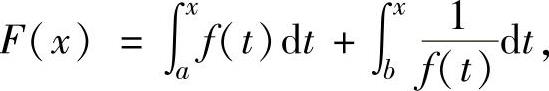
则方程F(x)=0在(a,b)内的实根个数为( ).
A.1 B.2 C.3 D.0
(15)设函数f(x)连续,则必为偶函数的是( ).
A.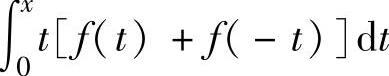 B.
B.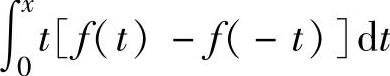
C.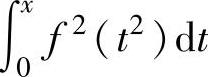 D.
D.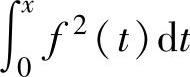
(16)设函数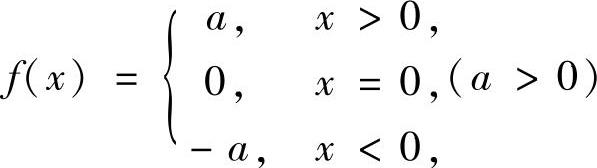 ,则函数
,则函数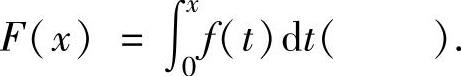
A.在点x=0处不连续(https://www.daowen.com)
B.在(-∞,+∞)上连续,但在点x=0处不可导
C.在(-∞,+∞)上可导,且F′(x)=f(x)
D.在(-∞,+∞)上可导,但不一定满足F′(x)=f(x)
(17)设f(x)是连续函数,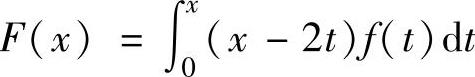 ,则当f(x)是单调增加的偶函数时,F(x)必为( ).
,则当f(x)是单调增加的偶函数时,F(x)必为( ).
A.单调增加的偶函数 B.单调减少的偶函数
C.单调增加的奇函数 D.单调减少的奇函数
(18)设函数y=f(x)在[-1,3]上的图形如图题2.1.18所示,
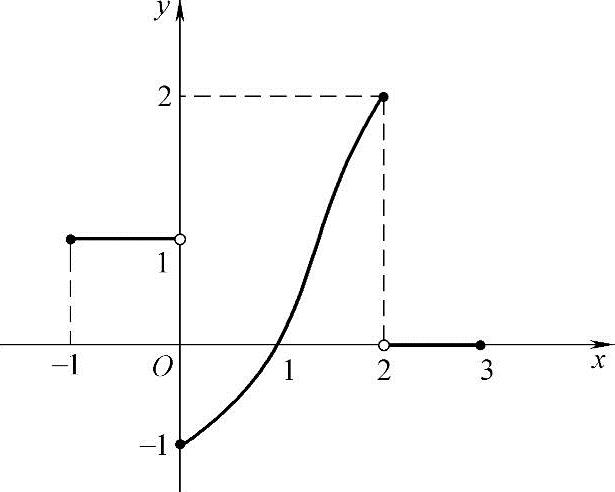
图题2.1.18
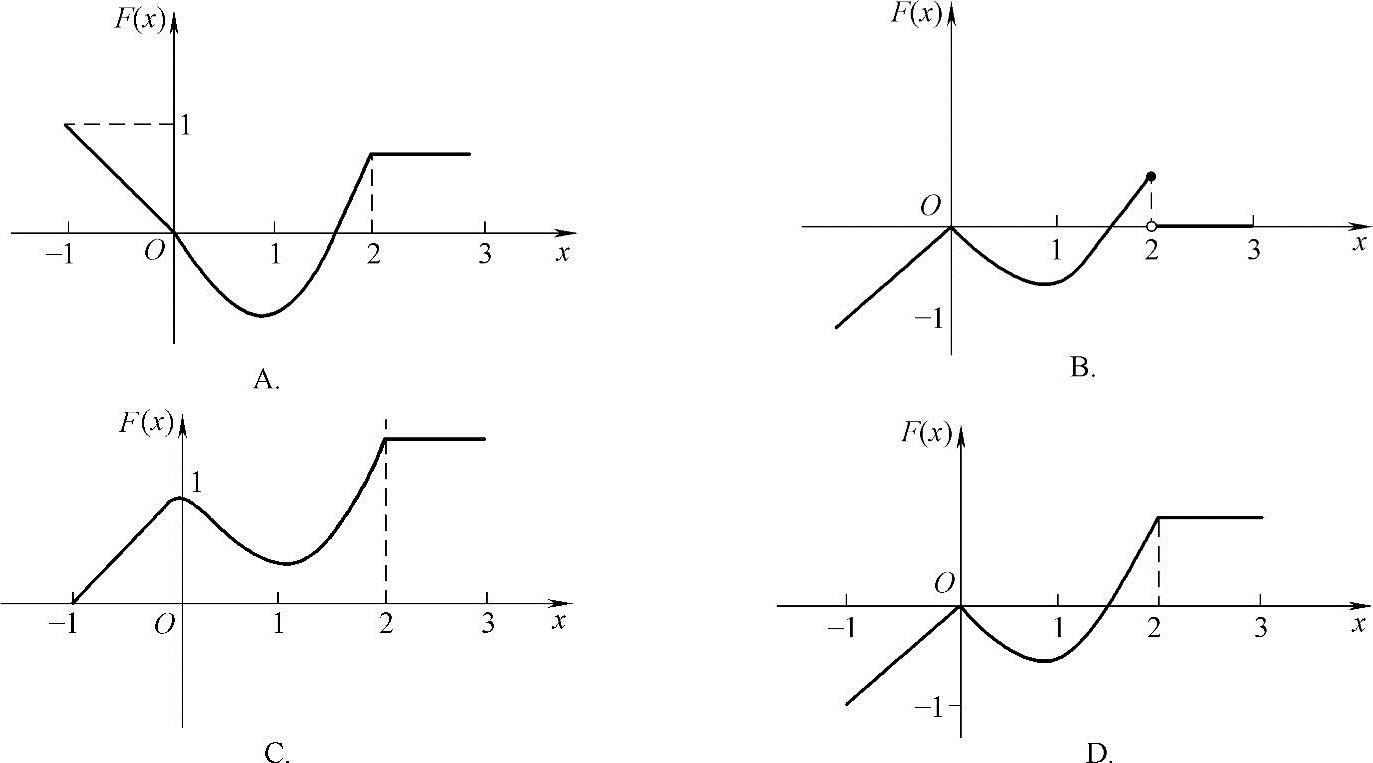
则函数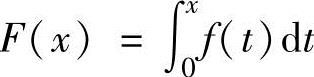 的图形为( ).
的图形为( ).
(19)设f(x)是(-∞,+∞)上的连续奇函数,则().
A.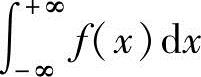 收敛B.当
收敛B.当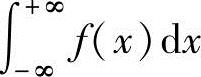 收敛时,其值必为零
收敛时,其值必为零
C.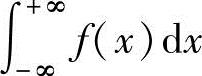 发散D.当
发散D.当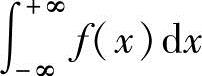 收敛时,其值未必不为零
收敛时,其值未必不为零
(20)由曲线y=(x+1)x(x-2)(-1≤x≤2)与x轴围成的平面图形面积的积分表达式为( ).
A.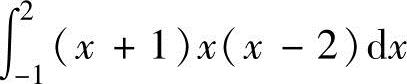 B.
B.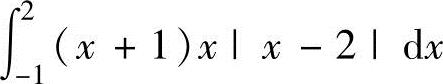
C.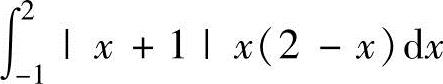 D.
D.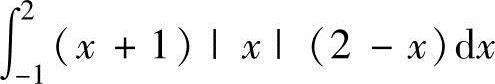
(21)由曲线y=x3-2x与y=x2(x≥0)围成的平面图形绕x轴旋转一周而成的旋转体体积的积分表达式为( ).
A.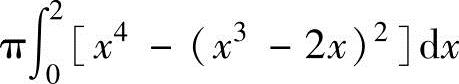
B.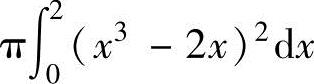
C.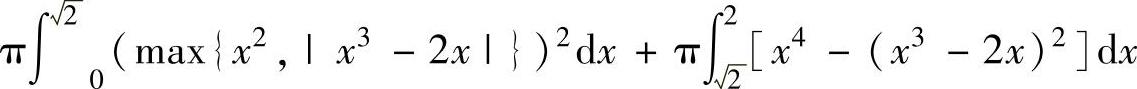
D.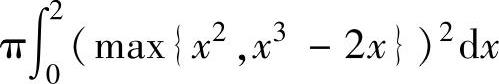
(22)设曲线y=min{ex,e-2x},记位于该曲线与x轴之间及直线x=t左边的平面图形面积为A(t),则A(t)=( ).
A.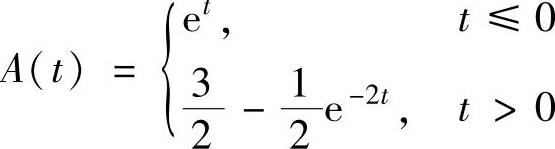 ,B.
,B.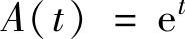
C.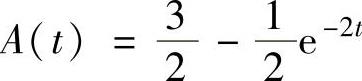 D.
D.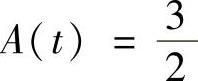
2.解答题
(1)设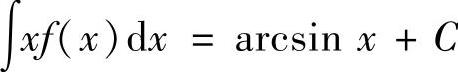 ,求不定积分
,求不定积分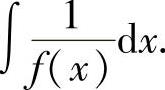
(2)设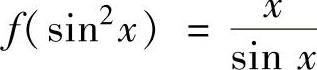 ,求
,求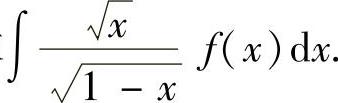
(3)求不定积分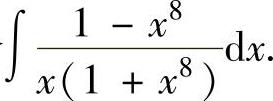
(4)求不定积分∫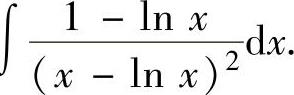
(5)求不定积分∫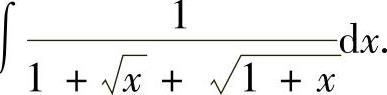
(6)设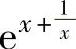 是函数f(x)的一个原函数,求不定积分∫
是函数f(x)的一个原函数,求不定积分∫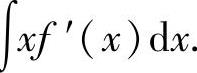
(7)已知y=f(x)单调可导,且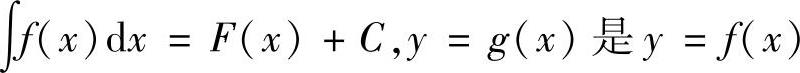 的反函数,求
的反函数,求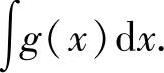
(8)设F(x)是函数f(x)的一个原函数,且当x≥0时f(x)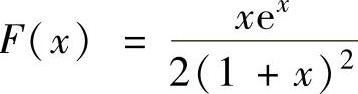 以及F(0)=1,求F(x)的表达式.
以及F(0)=1,求F(x)的表达式.
(9)求定积分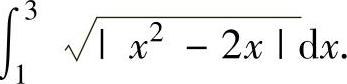
(10)求定积分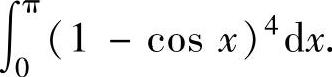
(11)求定积分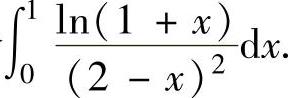
(12)求定积分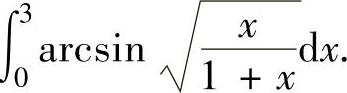
(13)设函数f(x)二阶连续可导,且f(0)=1,f(2)=3,f′(2)=5,求定积分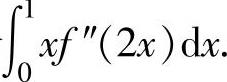
(14)设函数y=y(x)由方程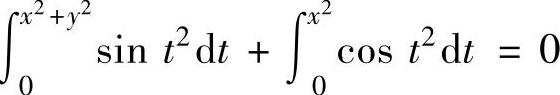 确定,求
确定,求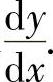
(15)设函数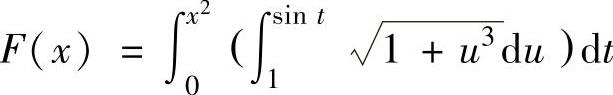 ,求
,求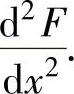
(16)设函数f(x)满足f(x)=f(x-1)+ln(1+x),且在[0,1]上f(x)=xex,求定积分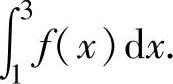
(17)设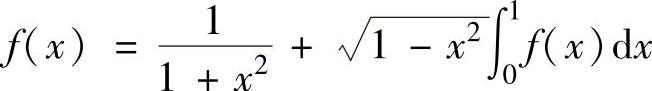 ,求定积分
,求定积分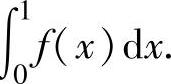
(18)求广义积分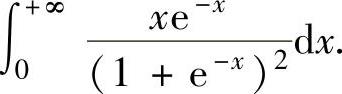
(19)求广义积分∫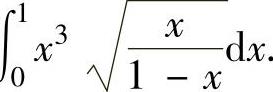
(20)设函数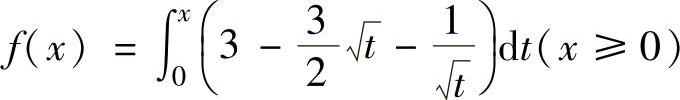 ,求由曲线y=f(x)及x轴围成的平面图形面积A.
,求由曲线y=f(x)及x轴围成的平面图形面积A.
(21)求曲线y=sinx(0≤x≤2π)和x轴围成的平面图形绕y轴旋转一周而成的旋转体体积V.
(22)求由曲线y=x2及y=1-x2围成的平面图形绕直线y=1旋转一周而成的旋转体体积V.
(23)设位于曲线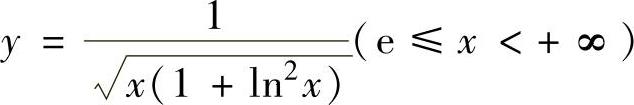 下方、x轴上方的无界区域为G,求G
下方、x轴上方的无界区域为G,求G
绕x轴旋转一周所得的空间区域的体积V.
