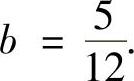平面图形面积的计算
【主要内容】
1.由曲线y=f1(x),y=f2(x)(其中,函数f1(x),f2(x)连续),直线x=a,x=b(a<b)围成的平面图形面积为
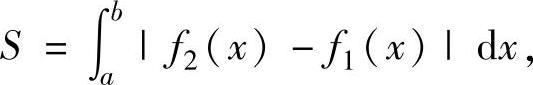
特别地,由曲线y=f(x)(其中,f(x)是非负连续函数),直线x=a,x=b(a<b)围成的平面图形(曲边梯形)面积为
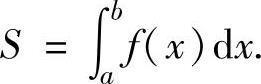
2.由曲线x=g1(y),x=g2(y)(其中,函数g1(y),g2(y)连续),直线y=c,y=d(c<d)围成的平面图形面积为
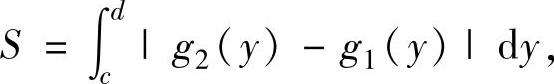
特别地,由曲线x=g(y)(其中,g(y)是非负连续函数),直线y=c,y=d(c<d)围成的平面图形(曲边梯形)面积为
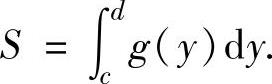
【典型例题】
例2.12.1 (单项选择题)连续函数y=f(x)在区间[-3,-2],[2,3]上的图形分别为直径是1的上、下半圆周,在区间[-2,0],[0,2]上的图形分别为直径是2的下、上半圆周(见
图2.12.1).设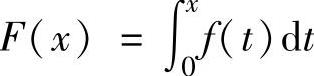 ,则下列结论正确的是( ).
,则下列结论正确的是( ).
A.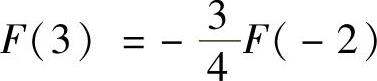
B.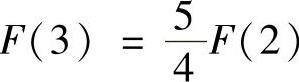
C.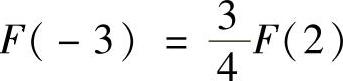
D.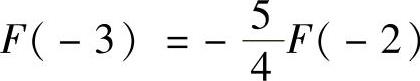
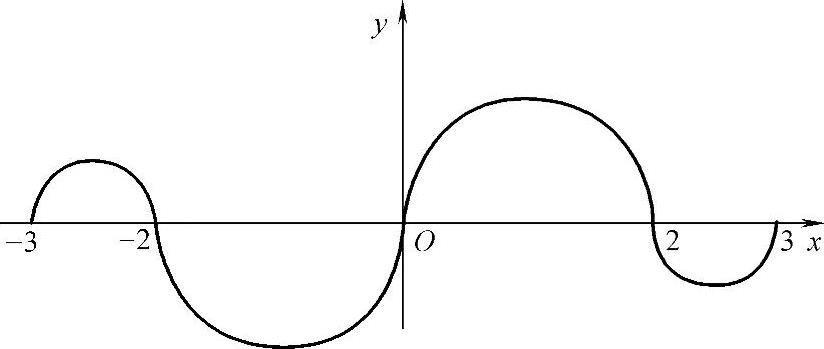
图 2.12.1
精解 算出F(3),F(-3),F(2)即可确定正确的选项.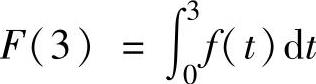 (它是[0,2]上的上半圆的面积与[2,3]上的下半圆面积的差)
(它是[0,2]上的上半圆的面积与[2,3]上的下半圆面积的差)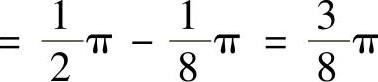 ,
,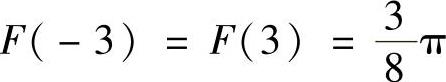 (由于f(x)是奇函数,所以F(x)是偶函数),
(由于f(x)是奇函数,所以F(x)是偶函数),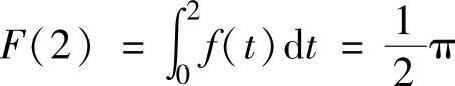 (它是[0,2]上的上半圆的面积).
(它是[0,2]上的上半圆的面积).
由此可知,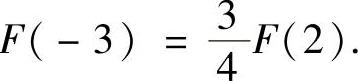
因此本题选C.
例2.12.2 求抛物线y2=2x与其上一点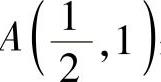 处的法线围成的平面图形D的面积S.
处的法线围成的平面图形D的面积S.
精解 先写出法线方程,然后画图计算图形D的面积S.
由于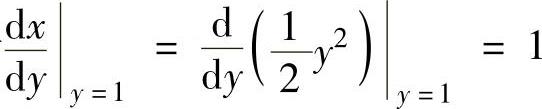 ,所以抛物
,所以抛物
线y2=2x在点A处的法线方程为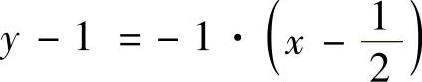 ,即
,即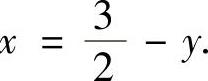
D的图形如图2.12.2所示,它是由曲线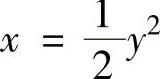 ,
,
直线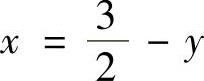 围成的,所以由该图可得
围成的,所以由该图可得
 (https://www.daowen.com)
(https://www.daowen.com)
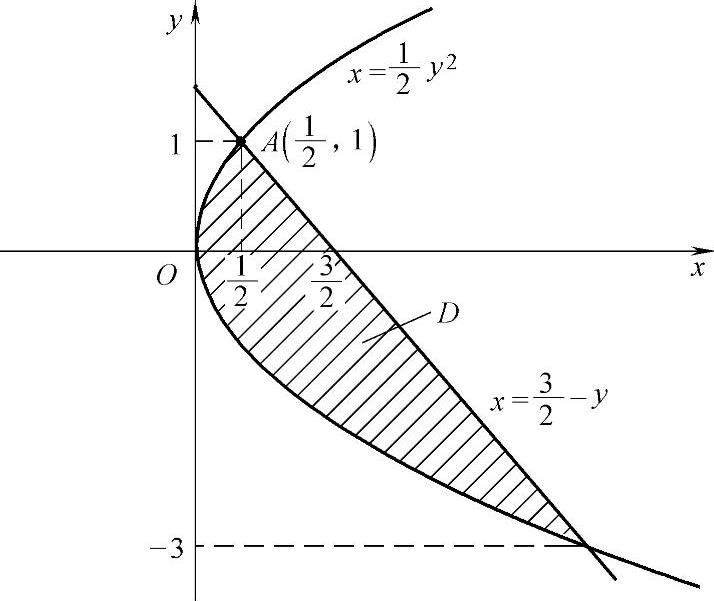
图 2.12.2
例2.12.3 求两椭圆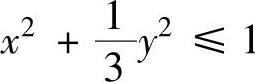 和
和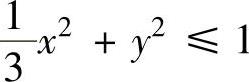 公共部分D的面积S.
公共部分D的面积S.
精解 D的图形如图2.12.3所示.由对称性知D在各个象限的面积相等,所以
S=4S1,
其中,S1是D在第一象限部分D1的面积.
记两椭圆的边界在第一象限的交点为A,则点A的坐标(x,y)满足
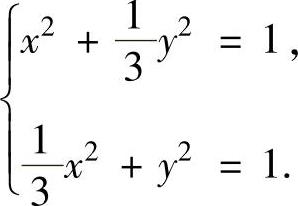
解此方程组得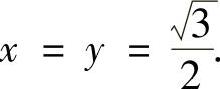
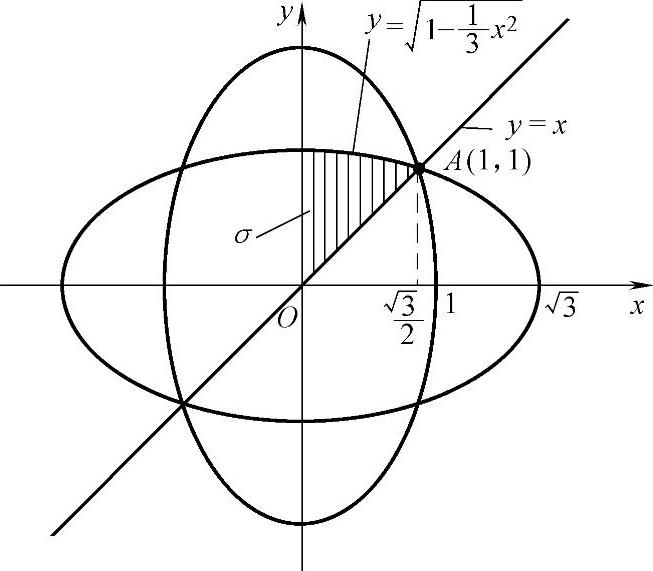
图 2.12.3
直线OA∶y=x将D1分成面积相等的两部分.记其中位于OA上方部分的面积为σ,由于
这一部分是由曲线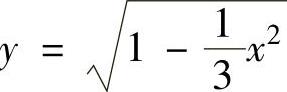 ,直线y=x和x=0围成(见图2.12.3阴影部分),所以
,直线y=x和x=0围成(见图2.12.3阴影部分),所以
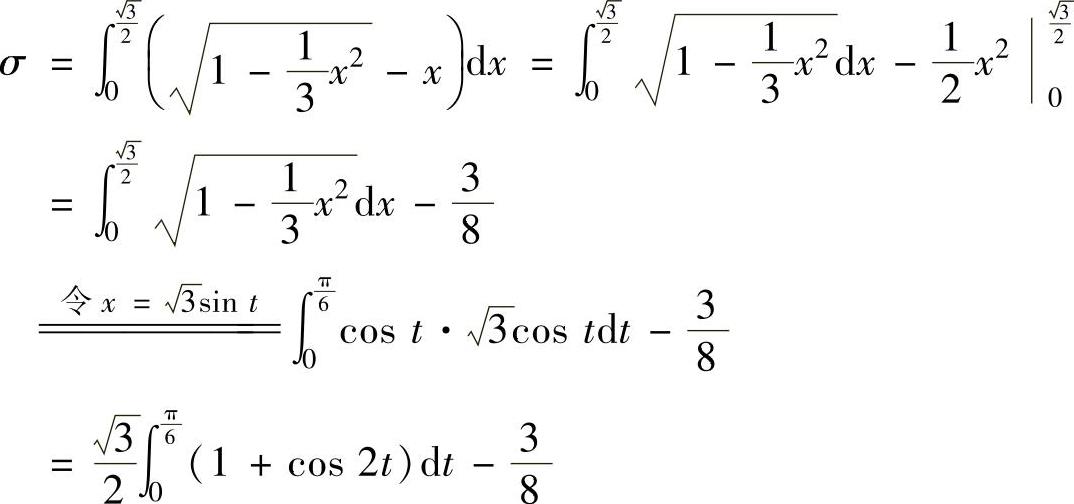
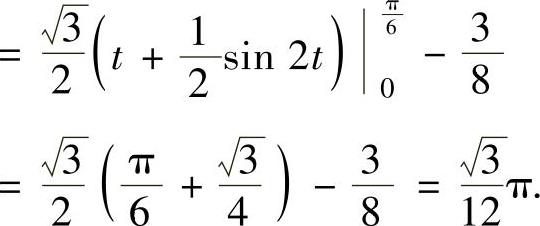
因此,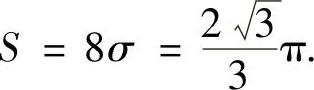
例2.12.4 设曲线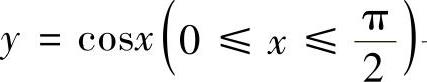 与x轴和
与x轴和
y轴围成的平面图形D被曲线y=asinx和y=bsinx(0<b<a)三等分,求常数a,b的值.
精解 图形D及曲线y=asinx,y=bsinx如图2.12.4所示.
由于D的面积为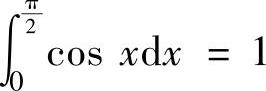 ,所以由题设知,由
,所以由题设知,由
曲线y=cosx,y=asinx及y轴围成的图形面积为
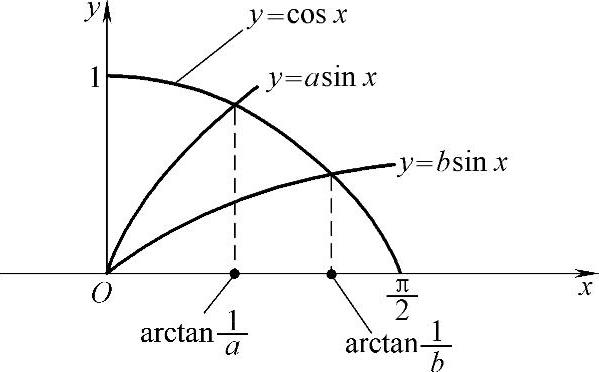
图 2.12.4
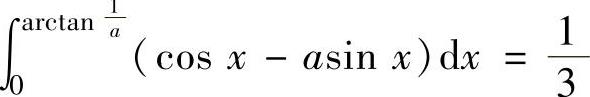 ,即
,即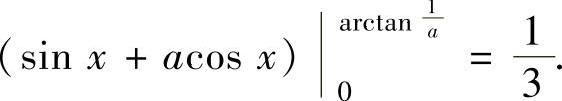
由此得到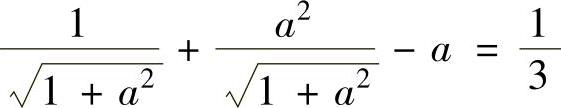 ,即
,即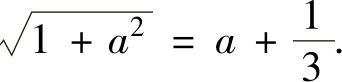
解此方程得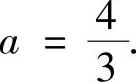
同样由题设知,由曲线y=cosx,y=bsinx及y轴围成的图形面积为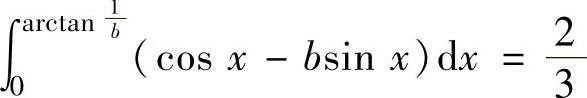 ,即
,即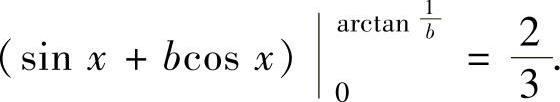
由此得到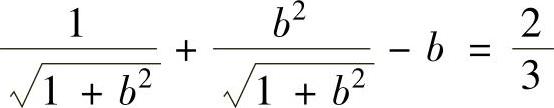 ,即
,即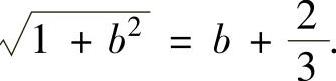
解此方程得