切比雪夫不等式
2026年01月14日
十九
、切比雪夫不等式
【主要内容】
切比雪夫不等式
设随机变量X的数学期望EX和方差DX都存在,则对任意ε>0,有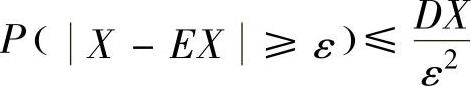 或
或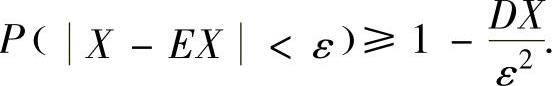
切比雪夫不等式可以用来估计某个随机变量X(仅知EX与DX,而未知X的分布)在以EX为中心的对称区间上取值的概率.
【典型例题】
例7.19.1 从发芽率为0.95的一批种子里随机取400粒,用切比雪夫不等式估计其不发芽的种子在15粒与25粒之间的概率.
精解 设随机变量X为400粒种子中不发芽的种子数,则X~B(400,0.05),并且EX=400×0.05=20,DX=400×0.05×(1-0.05)=19,于是由切比雪夫不等式知
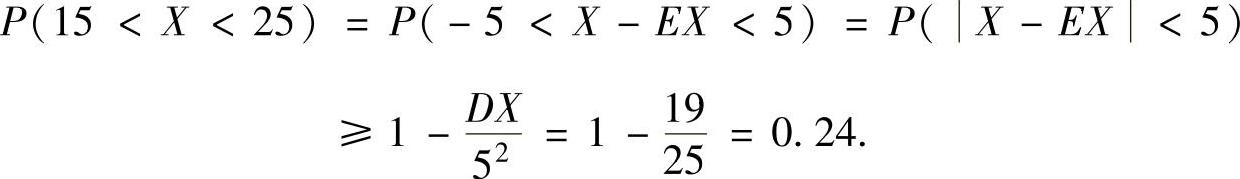
例7.19.2 设随机变量X,Y的数学期望分别为-2,2,方差分别为1,4,而相关系数为-0.5.用切比雪夫不等式估计概率P(X+Y≥6).
精解 记Z=X+Y,则
EZ=EX+EY=0,
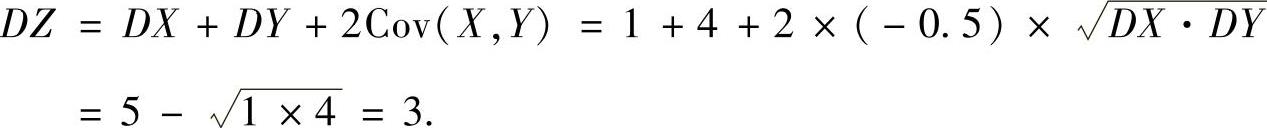
所以,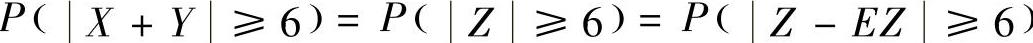
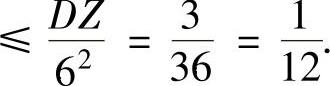 (https://www.daowen.com)
(https://www.daowen.com)
例7.19.3 设随机变量X~N(1,1),Y~N(0,1),且E(XY)=-0.1.用切比雪夫不等式估计概率P(-4<X+2Y<6).
精解 记Z=X+2Y,则
EZ=EX+2EY=1+2×0=1,
DZ=DX+4DY+4Cov(X,Y)
=1+4×1+4[E(XY)-EX·EY]
=5+4(-0.1-1×0)=4.6,
所以,由切比雪夫不等式得
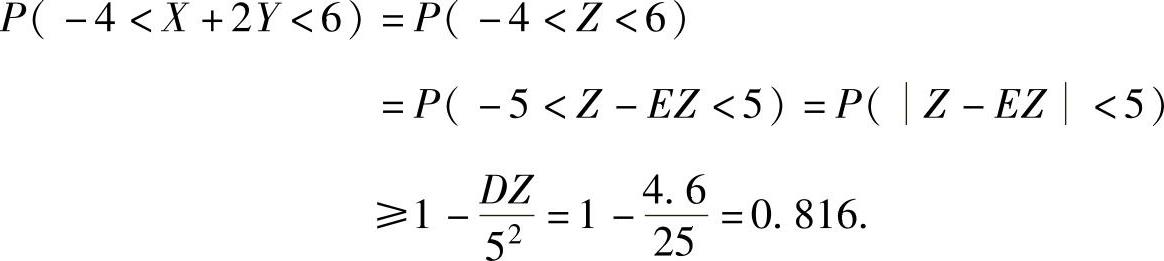
例7.19.4 设二维随机变量(X,Y)在圆域D:x2+y2≤4上服从均匀分布,用切比雪夫不等式估计概率P(XY≥1).
精解 应先算E(XY)与D(XY),由(X,Y)的概率密度为f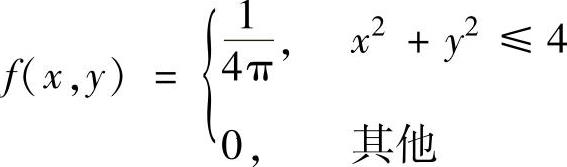 ,知
,知
D(XY)=E(XY-E(XY))2=E(X2Y2)

由于(X,Y)在D上服从均匀分布,所以P(XY≥1)=P(XY≤-1),从而