练习题七
1.单项选择题
(1)设A,B,C是事件,且P(AB-C)=0,0<P(C)<1,则必有( ).
A.P(A∪BC)=P(A∪B)B.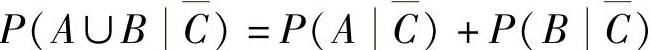
C.P(A∪BC)=P(AC)+P(BC)D.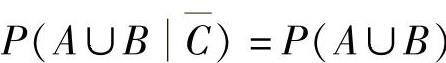
(2)设A,B,C是事件,且P(AB)=P(A)P(B),0<P(B)<1,0<P(C)<1,则必有( ).
A.P(ABC)=P(AC)P(BC)B.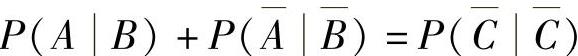
C. D.
D.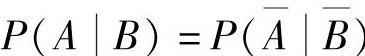
(3)设A1,A2,B是事件,且P(B)>0,A1A2=,则下列命题中不正确的是( ).
A.P(A1∪A2B)=P(A1B)+P(A2B)B.P(A1A2B)=
C.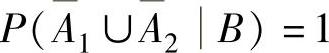 D.
D.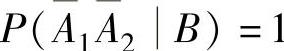
(4)设A,B,C是相互独立事件,且0<P(C)<1,AC≠,则下列4组事件中不独立的是( ).
A.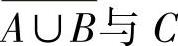 B.
B.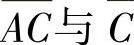
C.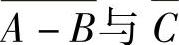 D.
D.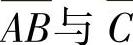
(5)设A1,A2,B都是事件,且0<P(B)<1及P(A1∪A2B)=P(A1B)+P(A2B),则( ).
A.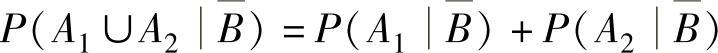 B.
B.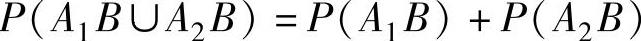
C.P(A1∪A2)=P(A1B)+P(A2B)D.P(B)=P(A1)P(BA1)+P(A2)P(BA2)
(6)袋中有7个乒乓球,其中2个黄球3个白球及2个黑球,今有两个人依次随机各取一球,取后不放回,则第二个人取到黄球的概率与第二个人才取到白球的概率分别为( ).
A.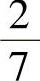 ,
,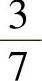 B.
B.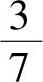 ,
,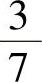
C.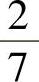 ,
,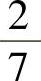 D.
D.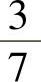 ,
,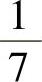
(7)已知A,B是相互独立的事件,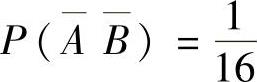 ,
,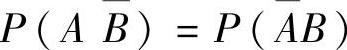 ,则P(A)=( ).
,则P(A)=( ).
A.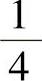 B.
B.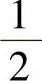 C.
C.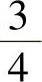 D.1
D.1
(8)已知A,B是事件,满足P(A)=0.4,P(AB)=0.2,P(AB)=P(AB),则P(A∪B)=().
A.0,2 B.0.5 C.0.7 D.0.9
(9)欲使f(x)=cosx,x∈[a,b],
{0,其他为随机变量X的概率密度,则[a,b]应为( ).
A.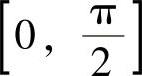 B.
B.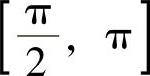
C.[0,π]D.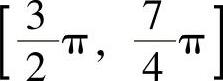
(10)设F(x)是连续型随机变量X的分布函数,f(x)是X的概率密度,已知X与-X有相同的概率分布,则
A.F(x)=F(-x) B.F(x)=-F(x)
C.f(x)=f(-x) D.f(x)=-f(x)
(11)随机变量Y=aX+b(a≠0)与随机变量X服从同一名称的分布,则X服从( ).
A.二项分布 B.泊松分布 C.正态分布 D.指数分布
(12)设对任意常数a,b(a<b),随机变量X满足
P(X>a)=1-α,P(X≤b)=1-β,则P(a<X≤b)=p满足( ).
A.p=1-(α+β) B.p≥α+β
C.p>1-(α+β) D.p<α+β
(13)设Z为连续型随机变量,其分布函数为FZ(z),X~U[0,1],则随机变量Y=FZ-1(X)的分布函数为( ).
A.FZ-1(y) B.FZ(y) C.1-FZ-1(y) D.1-FZ(y)
(14)设随机变量X~B(2,p),Y~B(3,p),若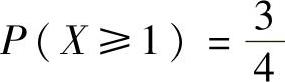 ,则P(Y≥1)=( ).
,则P(Y≥1)=( ).
A.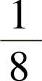 B.
B.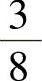
C.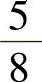 D.
D.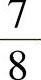
(15)设随机变量X~E(λ),则概率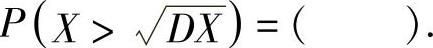
A.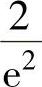 B.
B.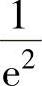
C.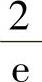 D.
D.
(16)一边长为1的正方体容器盛有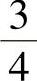 的液体.设一个小孔出现在容器的六个侧面的任
的液体.设一个小孔出现在容器的六个侧面的任
何一个部位都是等可能的.现容器侧面出现一个小孔,液体经此小孔流出,最后剩余液体的液面高度X是一个随机变量,则其分布函数F(x)是( ).
A.连续型的 B.恰好有两个间断点
C.离散型的 D.恰好有一个间断点
(17)设随机变量X~N(μ,σ2),且以y为未知数的二次方程y2+4y+X=0无实根的概率为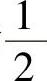 ,则μ=( ).
,则μ=( ).
A.0 B.1 C.2 D.4
(18)设随机变量X~N(μ,σ2),则概率P(X≤1+μ)( ).
A.随μ的增大而变大 B.随μ的增大而变小
C.随σ的增大而变大 D.随σ的增大而变小
(19)设随机变量X与Y相互独立,且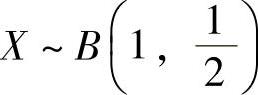 ,
,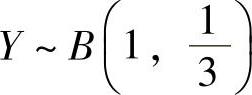 ,则二次方程t2+2Xt+Y=0有相同实根的概率为( ).
,则二次方程t2+2Xt+Y=0有相同实根的概率为( ).
A.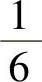 B.
B.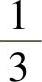
C.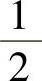 D.
D.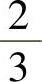
(20)设随机变量X与Y相互独立,且X~N(0,1),Y~N(1,1),则().
A.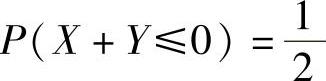 B.
B.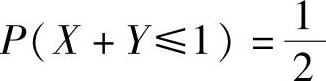
C.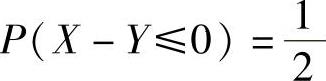 D.
D.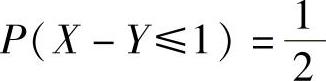
(21)设随机变量X,Y满足P(X≥0,Y≥0)=3
7,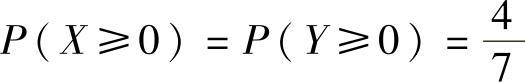 ,则P(max{X,Y}≥0)=( ).
,则P(max{X,Y}≥0)=( ).
A.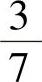 B.
B.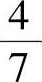
C.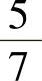 D.
D.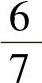
(22)设二维随机变量(X,Y)~N(0,0,1,1,0),则概率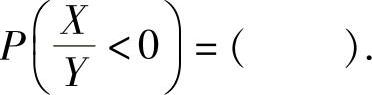
A.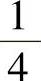 B.
B.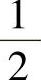
C.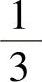 D.
D.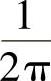 (https://www.daowen.com)
(https://www.daowen.com)
(23)设二维随机变量(X,Y)在D={(x,y)0≤x≤1,0≤y≤1}上服从均匀分布,则( ).
A.E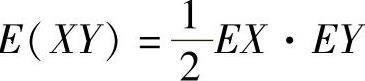 B.E(XY)=EX·EY
B.E(XY)=EX·EY
C.E(XY)=2EX·EY D.E(XY)=4EX·EY
(24)设X,Y都是随机变量,则D(X-2Y)=( ).
A.DX+4DY B.DX-4DY
C.DX+4DY-4Cov(X,Y) D.DX+DY+4Cov(X,Y)
(25)设随机变量X与Y相互独立,且EX=EY=0,DX=DY=1,则E(X+Y+1)2=( ).

(26)设二维随机变量(ξ,η)的概率密度为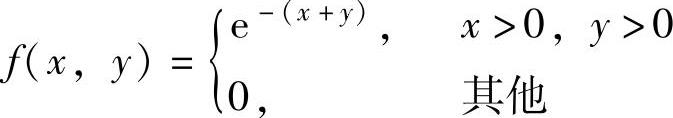 ,则随机变量
,则随机变量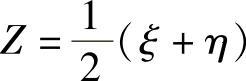 的概率密度φ(z)为( ).
的概率密度φ(z)为( ).
A.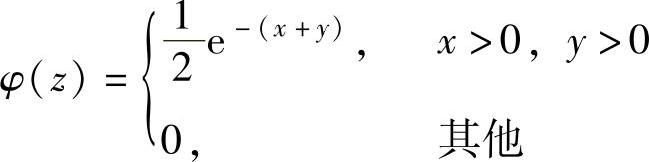 ,B.
,B.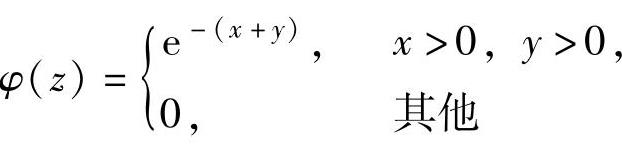
C.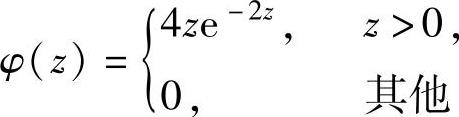 D.
D.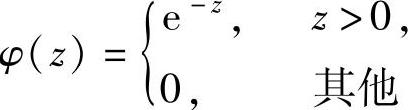
(27)设随机变量X~π(λ),且E((X-1)(X-2))=1,则参数λ=( ).
A.-2 B.-1 C.1 D.2
(28)现有10张奖券,其中8张2元的,2张5元的,今从中任取3张,则所得奖金的数学期望为( ).
A.6 B.12 C.7.8 D.9
(29)设二维随机变量(X,Y)服从二维正态分布,则随机变量ξ=X+Y与η=X-Y不相关的充分必要条件为( ).
A.EX=EY B.EX2-(EX)2=EY2-(EY)2
C.EX2=EY2 D.EX2+(EX)2=EY2+(EY)2
2.解答题
(1)在空战训练中甲机先向乙机开火,击落乙机的概率为0.2;若乙机未被击落,就进行还击,击落甲机的概率为0.3;若甲机未被击落,则再进攻乙机,击落乙机的概率是0.4,计算在两个回合中,乙机被击落的概率.
(2)袋中有4枚正品匀质硬币,2枚次品匀质硬币(次品硬币两面均印有国徽).在袋中任取一枚,将它投掷3次,已知每次都出现国徽,求此硬币是正品的概率.
(3)有10个相同的罐子,其中,有3个罐子中都装有1个黑球和1个红球,有6个罐子中都装有2个黑球和2个红球,有1个罐子中装有1个黑球和9个红球,现任取一个罐子,再从这个罐子中任取一球,结果发现取出的是红球.
(ⅰ)求此球是从装有10个球的罐子中取出的概率;
(ⅱ)此球最有可能是从装有几个球的罐子中取出的?
(4)设随机变量X的概率密度为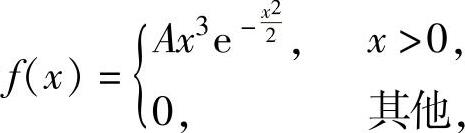 求常数A和X的分布函数F(x).
求常数A和X的分布函数F(x).
(5)考虑关于t的一元二次方程t2+Xt+Y=0,其中X,Y分别是将一颗骰子接连投掷两次先后出现的点数,求该方程有实根的概率p和有重根的概率q.
(6)已知随机变量X的分布律为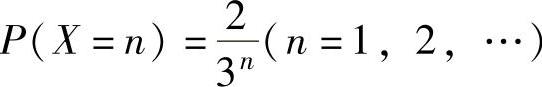 ,求随机变量Y=1+(-
,求随机变量Y=1+(-
1)X的分布律及分布函数F(y).
(7)设随机变量X的概率密度为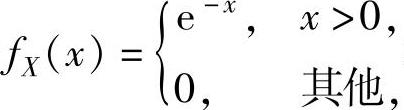 求随机变量
求随机变量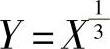 的概率密度fY(y).
的概率密度fY(y).
(8)设随机变量X的分布函数为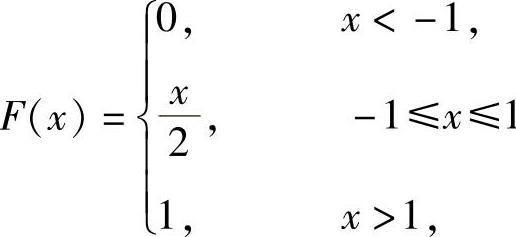 ,求Y=X2的分布函数FY(y).
,求Y=X2的分布函数FY(y).
(9)设某设备开机后无故障工作时间X服从参数为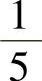 的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2h便自动关机.求该设备每次开机无故障工作时间Y的分布函数.
的指数分布.设备定时开机,出现故障时自动关机,而在无故障的情况下工作2h便自动关机.求该设备每次开机无故障工作时间Y的分布函数.
(10)设随机变量X与Y相互独立,且都服从U[0,3],求概率P(max{X,Y})≤1).
(11)设二维随机变量(X,Y)的概率密度为
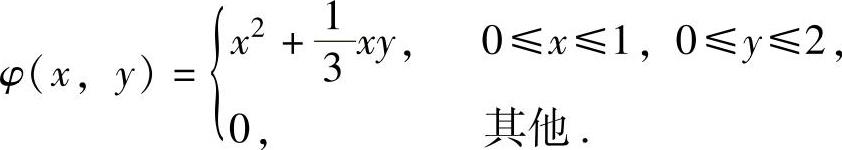
求:(ⅰ)(X,Y)的分布函数F(x,y);
(ⅱ)在Y=y(0≤y≤2)的条件下,关于X的条件概率密度φXY(xy).
(12)设平面区域D是曲线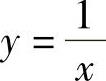 ,直线y=0,x=1,x=e2围成的,二维随机变量(X,
,直线y=0,x=1,x=e2围成的,二维随机变量(X,
Y)在D上服从均匀分布,求Y在X=2条件下的条件概率密度fYX(y2).
(13)设随机变量X与Y有相同的概率分布
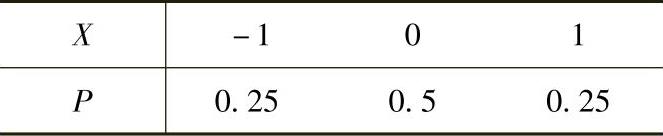
并且满足P(XY=0)=1,求概率P(X2=Y2)与P(Y·<X2).
(14)设独立重复试验中,每次成功的概率为p(0<p<1),X表示第一次成功之前失败的次数,Y表示前两次成功之间失败的次数,求二维随机变量(X,Y)的分布律,并问X与Y是否独立.
(15)设盒中有5个产品,其中有2个次品,现无放回地逐个检验,求:
(ⅰ)检验出第i个次品所需的检验次数Xi的分布律(i=1,2);
(ⅱ)二维随机变量(X1,X2)的分布律.
(16)设随机变量X的概率密度为 令Y=X2,F(x,y)是二维随机变量(X,Y)的分布函数,求:
令Y=X2,F(x,y)是二维随机变量(X,Y)的分布函数,求:
(ⅰ)Y的分布函数FY(y);
(ⅱ)F(1,4)的值.
(17)设二维随机变量(X,Y)的概率密度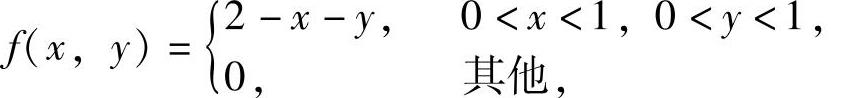
求:(ⅰ)概率P(X≥2Y);
(ⅱ)随机变量Z=X-Y的概率密度fZ(z).
(18)设随机变量X与Y相互独立,X的分布律为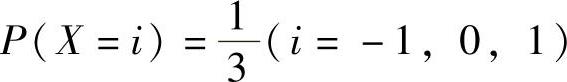 ,Y的
,Y的
概率密度为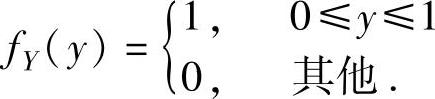 ,记Z=X+Y,求:
,记Z=X+Y,求:
(ⅰ)概率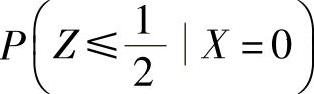 ;
;
(ⅱ)随机变量Z的概率密度fZ(z).
(19)设二维随机变量(X,Y)的概率密度为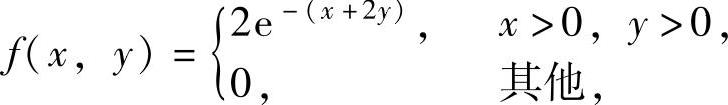 求随机变量Z=X+2Y的概率密度fZ(z).
求随机变量Z=X+2Y的概率密度fZ(z).
(20)设随机变量X的概率密度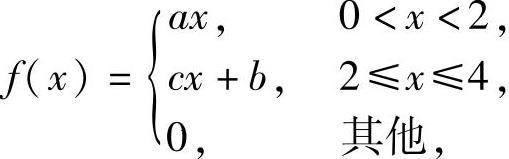 且EX=2,
且EX=2,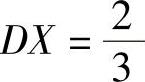 ,求常数a,b,c的值及随机变量Y=eX的数学期望EY.
,求常数a,b,c的值及随机变量Y=eX的数学期望EY.
(21)设随机变量(X,Y)在D={(x,y)0<x<1,0<y<x}上服从均匀分布,求Cov(X,Y).
(22)设X,Y是相互独立的随机变量,它们都服从参数为λ的泊松分布,求随机变量U=2X+Y,V=2X-3Y的相关系数.
(23)设随机变量X~U[-π,π],记Y=min{X,1},求随机变量Y的数学期望与方差.
(24)某箱装有100件产品,其中一、二、三等品的件数分别为80,10,10.现从中随机抽取一件,记 i=1,2.求随机变量X1与X2的相关系数ρ.
i=1,2.求随机变量X1与X2的相关系数ρ.
(25)某餐厅每天接待400名顾客.设每位顾客的消费额(元)在区间[20,100]上服从均匀分布,且顾客的消费是相互独立的.
(ⅰ)求该餐厅的日平均营业额;
(ⅱ)利用独立同分布中心极限定理求日营业额在平均营业额上下不超过760(元)的概率.
