附录 微积分在经济上的应用
【主要内容】
1.成本、收益与利润
某产品的总成本是指生产一定数量的产品所需的全部经济源投入的价格或费用的总额，记为C.它由固定成本C1与可变成本C2组成，其中固定成本C1是常数，可变成本是产品量Q的函数，即C2=C2（Q），于是，产品量为Q的产品的总成本是
C（Q）=C1+C2（Q）.
某产品的总收益是生产者出售一定数量产品所得的全部收入，记为R.它是出售的产品量Q的函数，即R=R（Q）.
某产品的总利润L为某总收益减去其总成本和上缴税金后的余额.在产销平衡和不计上缴税金的前提下，产品量为Q的产品总利润是
L（Q）=R（Q）-C（Q）.
2.边际与弹性
函数y=f（x）在点x处的导数f′（x）称为f（x）的变化率，也称f（x）的边际函数.例如，称总成本C（Q）的导数C′（Q）为边际成本；称总收益R（Q）的导数R′（Q）为边际收益.函数y=f（x）在x处的导数f′（x）与yx之比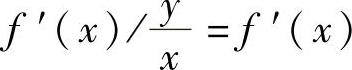
·
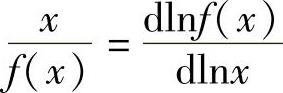，称为
f（x）的弹性函数，记为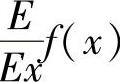
，即
E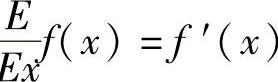
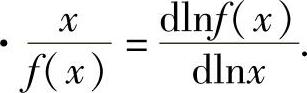例如，商品的需求函数
Q=f（P）（其中P为商品价格，Q为商品的需求值）对价格的弹性（简称为需求价格弹性）为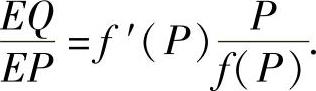
3.复利问题
设本金为P0，年利率为γ，则存款x年后，年复利的本利和为S=P0（1+γ）x；存款x年后，连续复利的本利和为S=P0eγx.
【典型例题】
例附1 设总成本C关于产品量x的函数为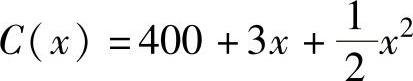
，价格P关于需求量
x的函数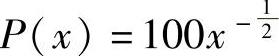
（假定供销平衡），求
（1）边际成本；
（2）边际收益；
（3）边际利润；
（4）收益价格的弹性（即收益对价格的弹性）.
精解 （1）边际成本C′（x）=3+x.
（2）收益函数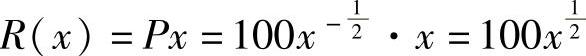
，所以边际收益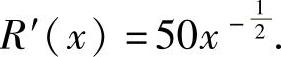
（3）利润函数L（x）=R（x）-C（x），所以边际利润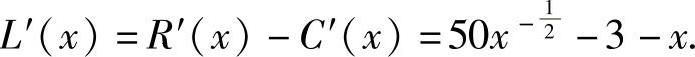
（4）由于收益对价格的函数为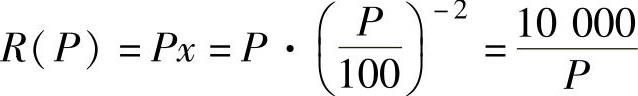
，
所以，收益价格的弹性
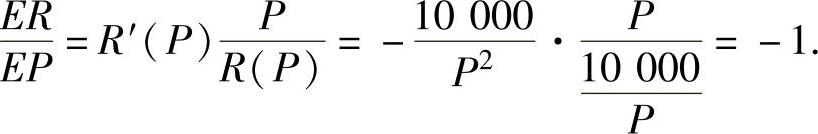
例附2 设某工厂生产x件产品的成本为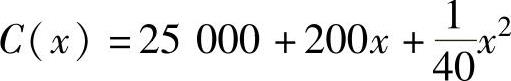
，问
（1）生产多少件产品，可使平均成本最小？
（2）如果每件产品以500元出售，则生产多少件产品，可获利最大？
精解 （1）平均成本函数为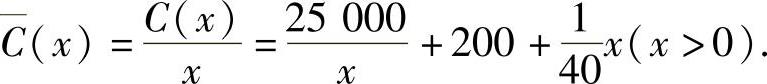
于是由
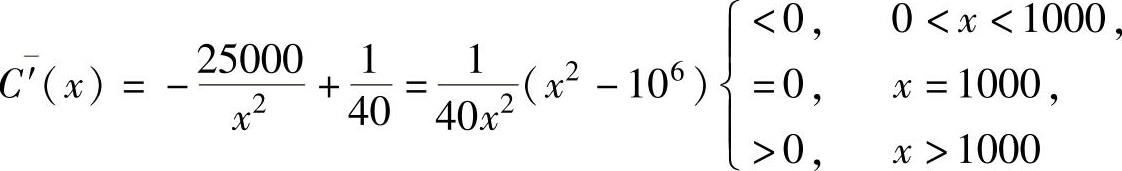
知，x=1000时C（x）取得最小值，即当生产1000件产品时，平均成本最小.
（2）利润函数为
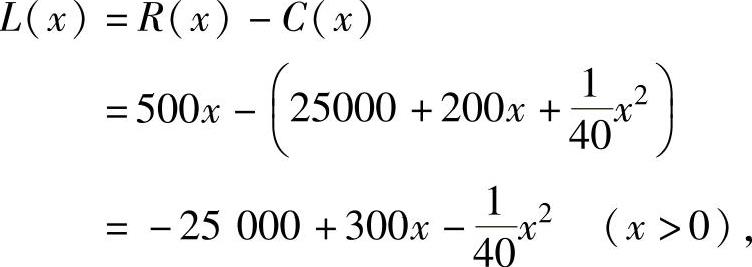
所以，由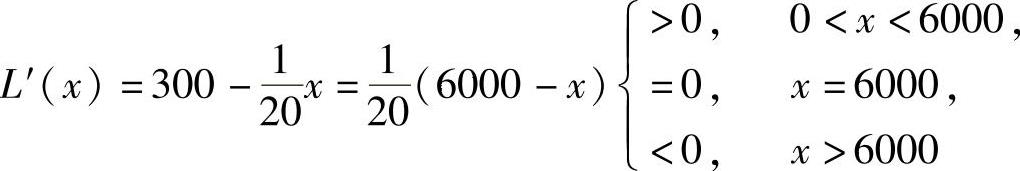
知x=6000时，L（x）取最大值，即如果每件产品以500元出售，则生产6000件产品时，可获利最大.
例附3 设产生某种产品的固定成本为50，产量为x时，边际成本函数C′（x）=x2-14x+111，边际收益函数为R′（x）=100-2x.
（1）求总利润函数；
（2）产量为多少时，总利润最大？
精解 （1）总利润函数L（x）=R（x）-C（x），
其中，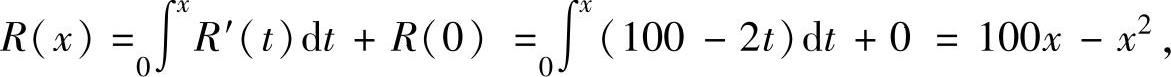
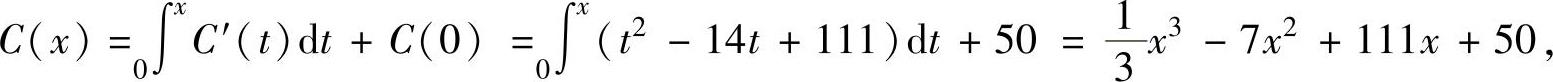
所以，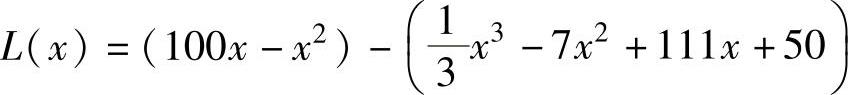
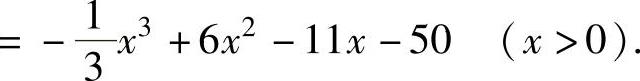
（2）L′（x）=R′（x）-C′（x）=（100-2x）-（x2-14x+111）
=-（x2-12x+11）=-（x-11）（x-1）=0，(https://www.daowen.com)
它的根为x=1，11.据此列表得
由表可知，L（x）在x=11处取到极大值，此外由于L（0）=-50，所以L（11）是最大值.因此当产量为11单位时，总利润最大.
注 题解中，是由比较L（11）与L（0）后才能确定x=11是最大值点.
例附4 设某商品的平均收益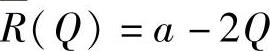
（常数a>0，Q为产量或需求量），总成本
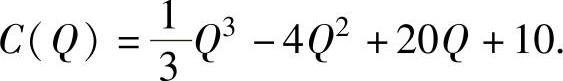已知需求价格弹性εp=-1.5时，总利润最大.求a与总利
润最大时的产量.
精解 设总利润最大时的产量为Q0，由于商品价格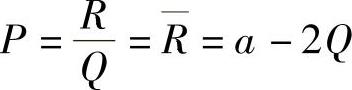
，即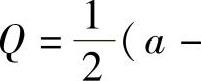
P）.于是由
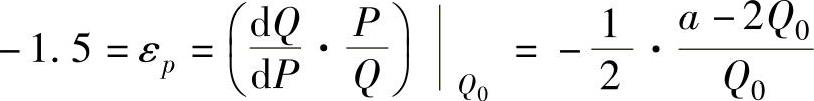
得a=5Q0.
下面计算Q0.
记总利润函数为L（Q），则，
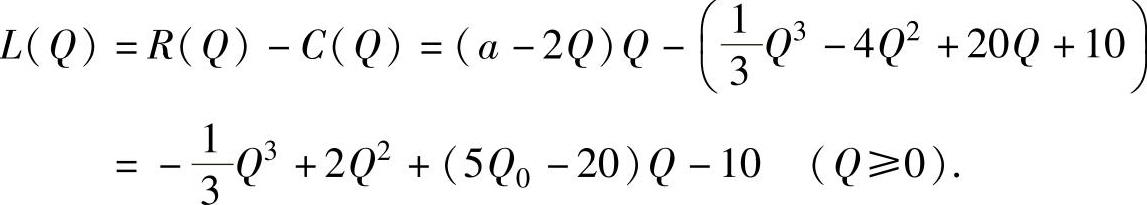
由于L（Q）在Q0（Q0>0）处取到最大值，所以有L′（Q0）=0，即Q20-9Q0+20=0，由此得到Q0=4，5.
显然，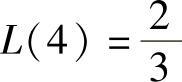
，
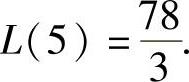所以Q0=5及a=25.因此，总利润最大时，常数a=25，且
产量为5.
例附5 已知当某种型号的游艇生产到第Q艘时，平均成本的边际函数为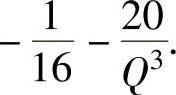
又
知每艘游艇的销售价为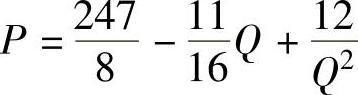
（万元），而每销售这种游艇一艘要纳税2万元，
此外，已知生产这种游艇2艘时的平均成本为6.25万元.问这种游艇生产多少艘才能获得最大利润？
精解 由题设知，平均成本函数
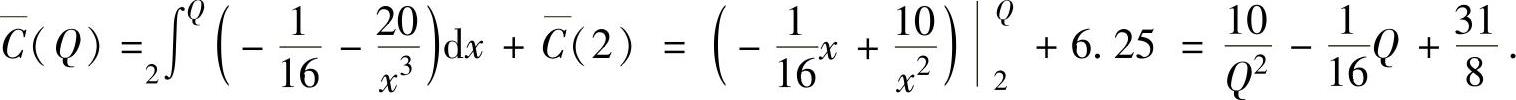
因此，总利润函数为
由于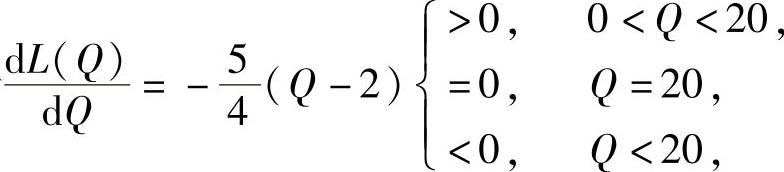
所以，Q=20时，L（Q）取得最大值，即当生产20艘艇才能获得最大的利润.
例附6 设某酒厂有批新酿的好酒，如果现在（设t=0）就出售，总收入为R0（元）.如果窖藏起来待来日按陈酒价格出售，t年末总收入为R（t）=R0e0.4t.假设银行利率为0.06，并以连续复利计算，试求窖藏多少年售出可使总收入的现值最大.
精解 这批酒在窖藏到t年末售出的总收入为R（t）时，其现值为
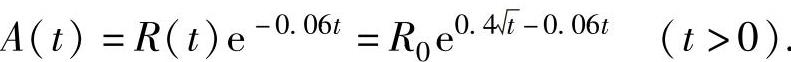
由于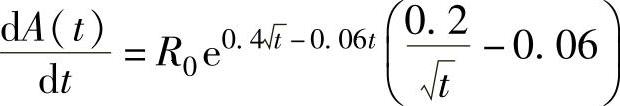
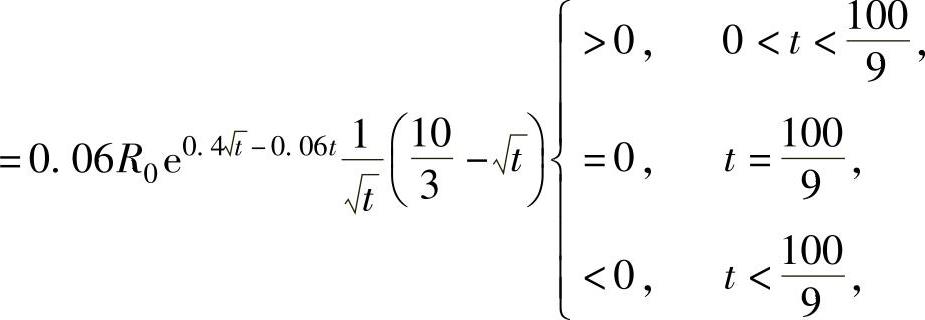
所以，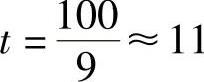
时，A（t）取最大值.因此，在窖藏约11年后售出可使总收入的现值
最大.
注 当本金为A，年利率为r时，存款t年后连续复利的本利和为Aert；当年利率为r，存款t年后的本利和为R（t）时，现值A=R（t）e-rt.
例附7 设银行存款的年利率为r=0.05，并依年复利计算以下问题：
某基金会希望通过存款A万元实现第一年末提取19万元，第二年末提取28万元，…，第n年末提取（10+9n）万元，并能按此规律一直提取下去，问A至少为多少万元？
精解 设第一年初存入本金A1万元，使第一年末时能提取19万元，则A1=（1+r）-1；
设第一年初存入本金A2万元，使第二年末时能提取28万元，则A2=28（1+r）-2︙
设第一年初存入本金An万元，使第n年末时能提取（10+9n）万元，则An=（10+9n）（1+r）-n，︙
于是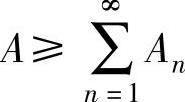
.下面计算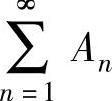
：
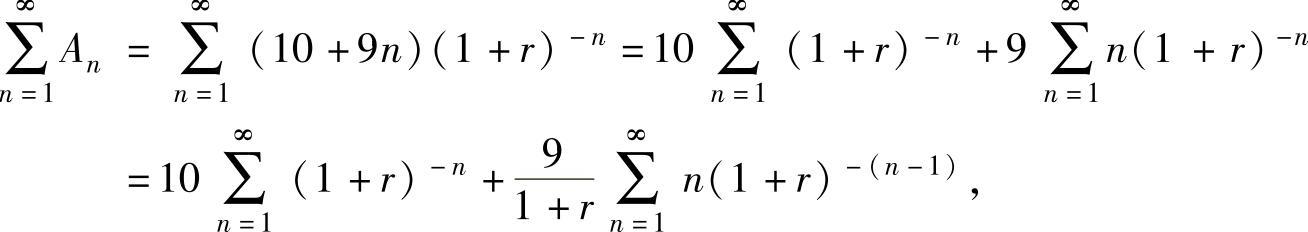
其中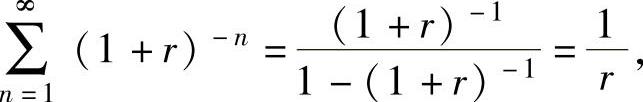
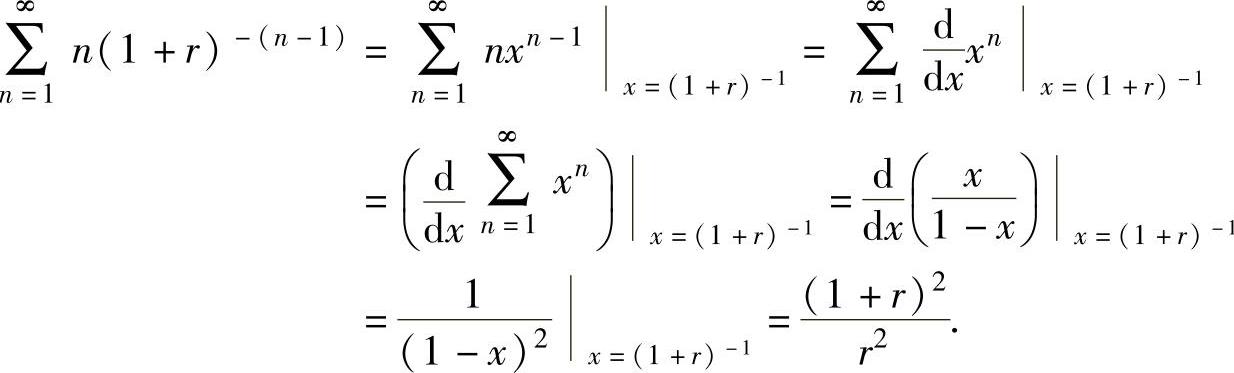
将它们代入式（1）得
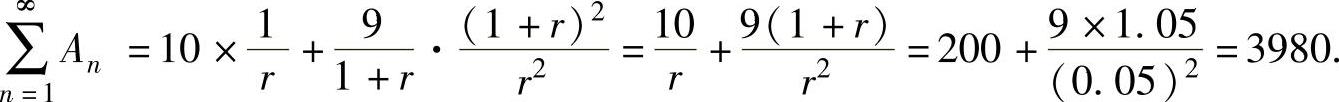
由此可知，A至少是3980万元，才能按题中所列规律一直提取下去.