练习题八解答
一、单项选择题
(1)D (2)A (3)C (4)B (5)D (6)C
(7)A (8)C (9)C (10)C (11)C (12)C
(13)B
2.解答题
(1)ES2=DX=EX2-(EX)2,(1)
其中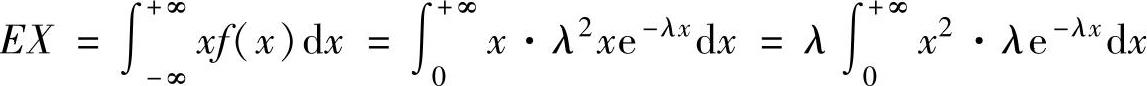 =λET2(其中T~E(λ))
=λET2(其中T~E(λ))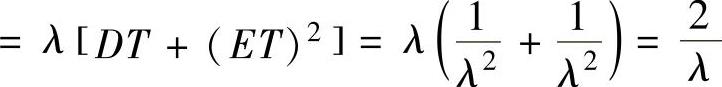 ,(2)
,(2)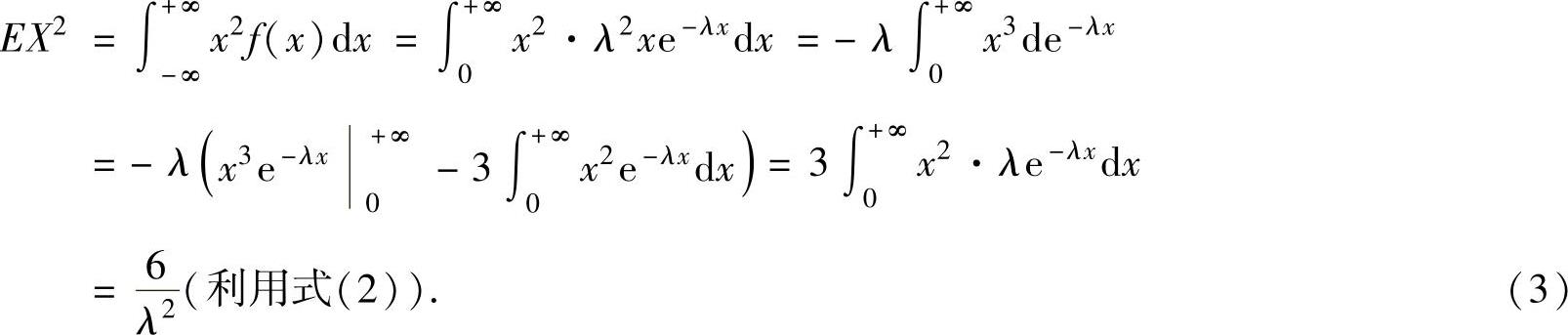
将式(2)、式(3)代入式(1)得
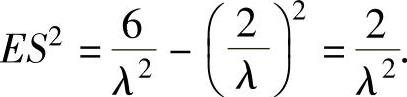
(2)由于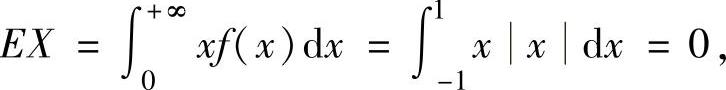
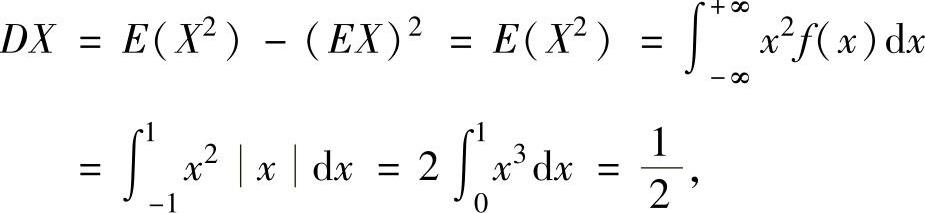
所以,由独立同分布中心极限定理得
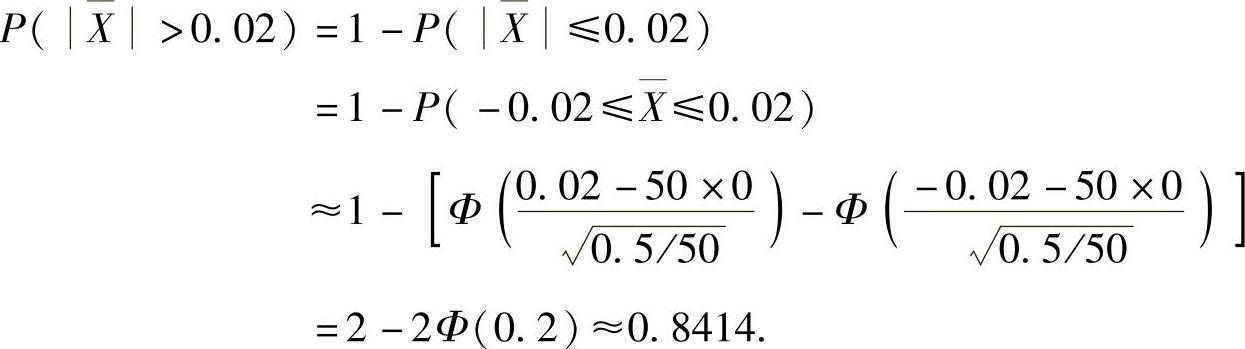
(3)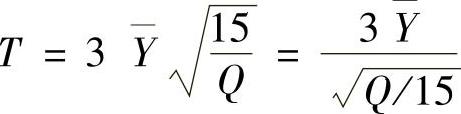 ,其中由
,其中由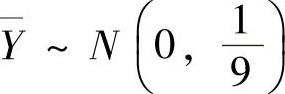 知
知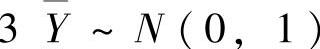 ,此外由
,此外由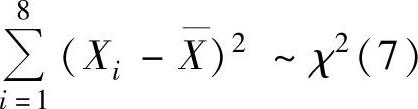 ,
,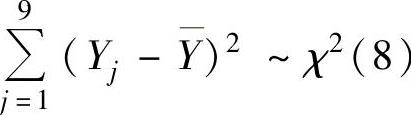 ,且
,且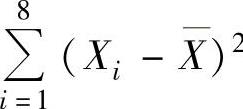 与
与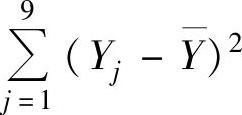 相互独立知
相互独立知
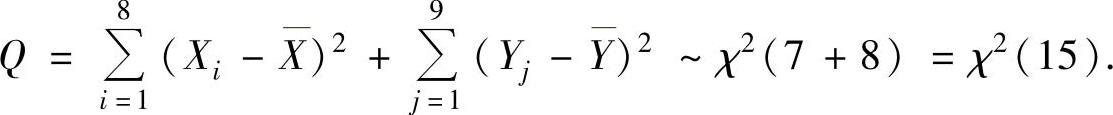
并且3Y与Q相互独立.因此由t分布的定义知T~t(15).
(4)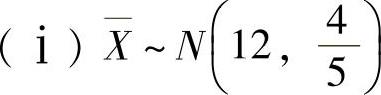 ,所以
,所以
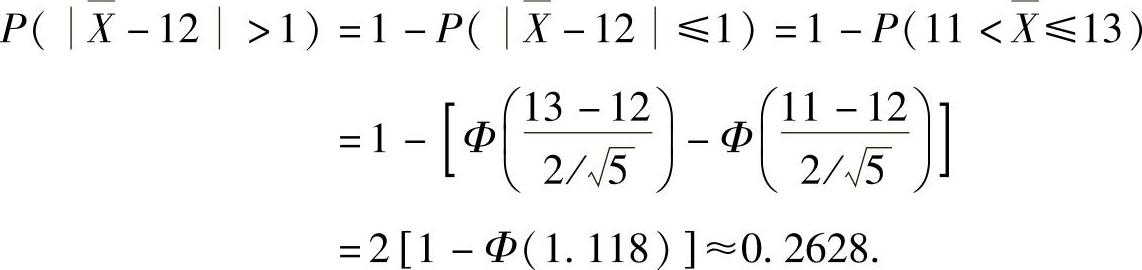
(ⅱ)P(max{X1,X2,…,X5}>15)=1-P(max{X1,X2,…,X5}≤15)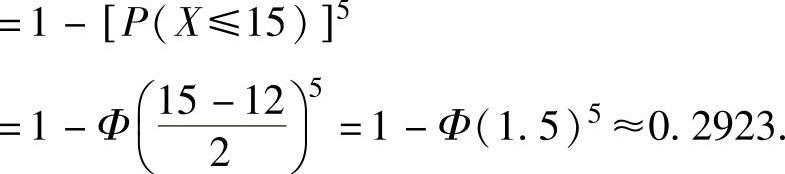
(5)(ⅰ)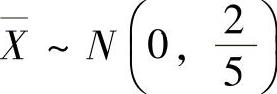 ,
,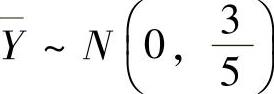 ,并且它们相互独立,所以Z=X-Y~N(0,1).
,并且它们相互独立,所以Z=X-Y~N(0,1).
(ⅱ)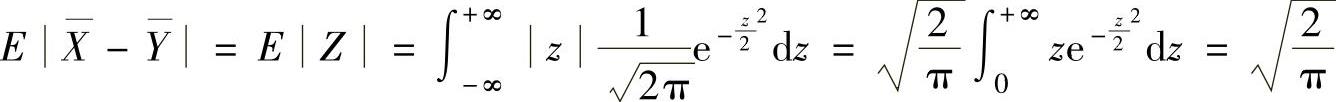 ,
,
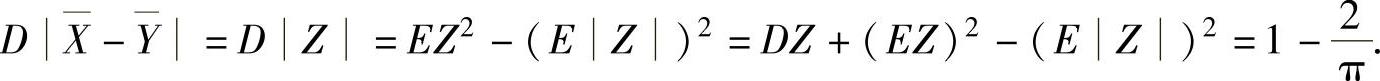
(6)由X与S2相互独立知X2与S4相互独立,所以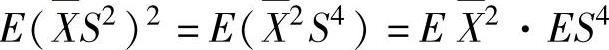 ,(1)其中,
,(1)其中,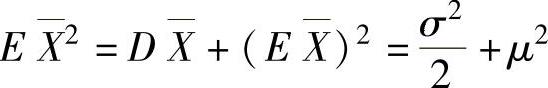 ,(2)
,(2)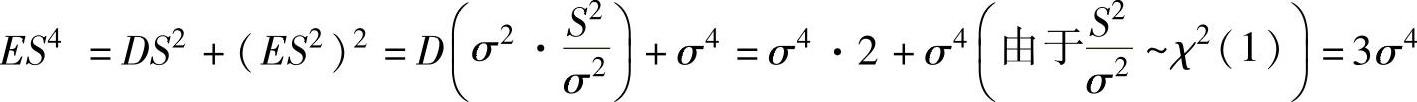 ,(3)
,(3)
将式(2)、式(3)代入式(1)得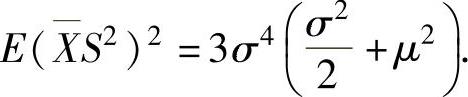
(7)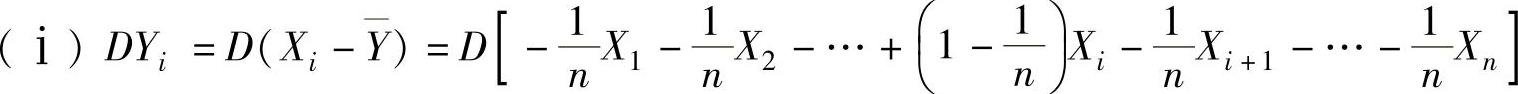
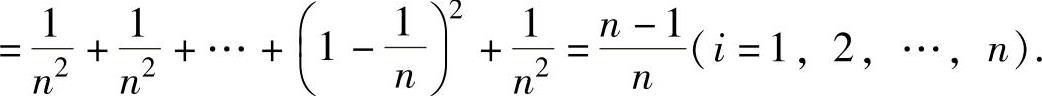 (https://www.daowen.com)
(https://www.daowen.com)
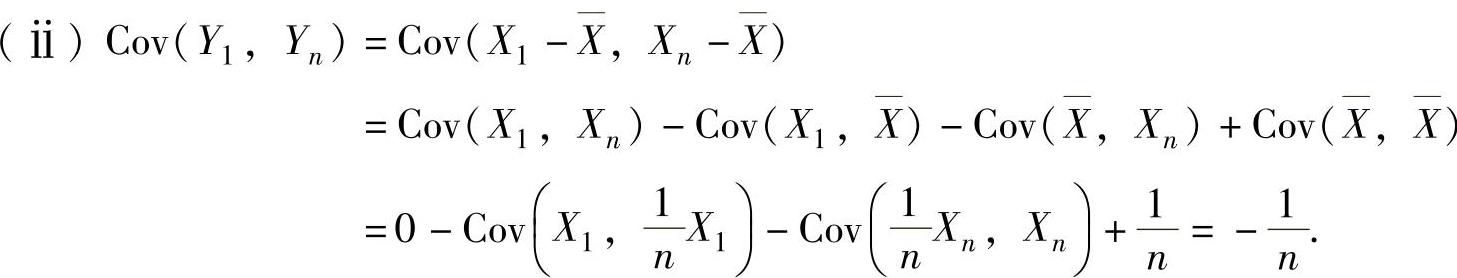
(8)X的分布律为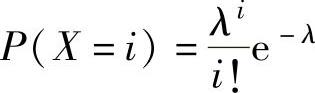 .于是似然函数为
.于是似然函数为
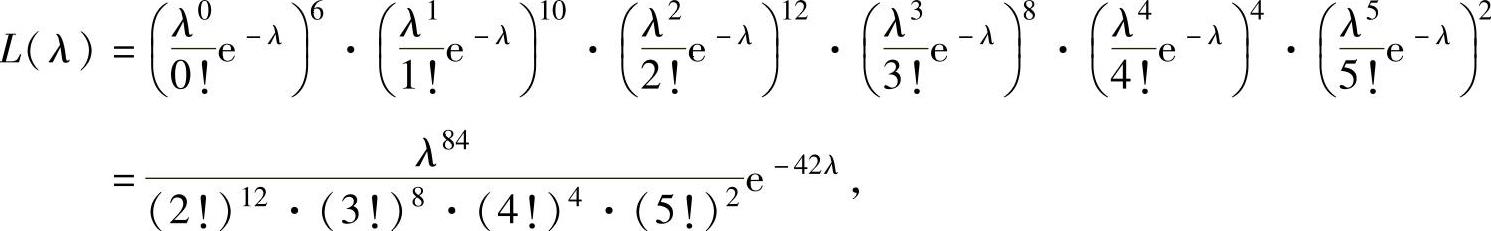
即 lnL(λ)=K+84lnλ-42λ(其中K=-ln[(2!)12·(3!)8·(4!)4·(5!)2]).
令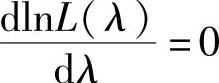 得λ的最大似然估计值λ^ =2.
得λ的最大似然估计值λ^ =2.
(9)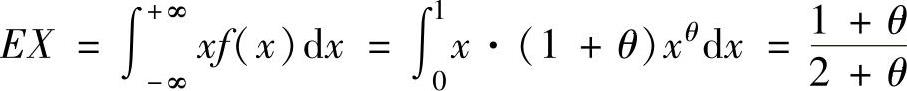 ,记样本均值为X.
,记样本均值为X.
令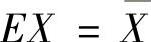 ,即
,即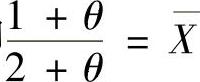 ,所以θ的矩估计量为
,所以θ的矩估计量为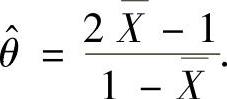
设样本观察值为x1,x2,…,xn,则似然函数为
L(θ)=(1+θ)x1θ·(1+θ)x2θ·…·(1+θ)xnθ
=(1+θ)n(x1x2…xn)θ,
lnL(θ)=nln(1+θ)+θln(x1x2…xn),
令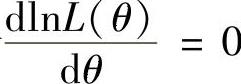 得
得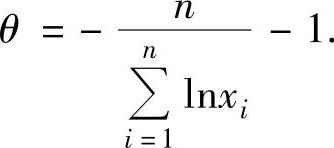 所以θ的最大似然估计量为
所以θ的最大似然估计量为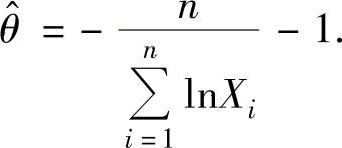
(10)(ⅰ)X的分布函数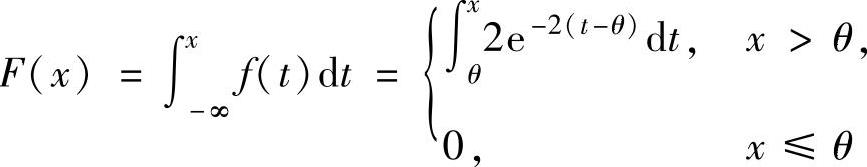
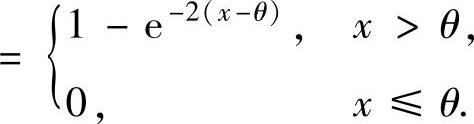
(ⅱ)θ^的分布函数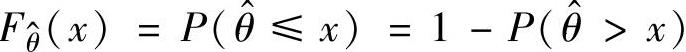
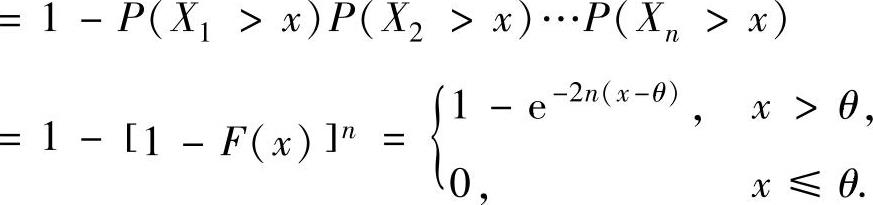
(ⅲ)由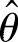 的概率密度
的概率密度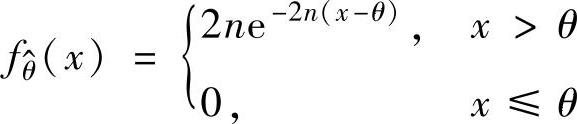 ,知
,知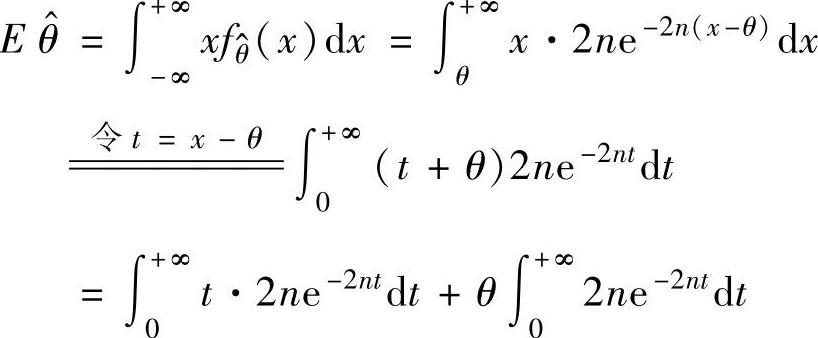
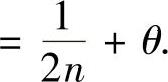
(11)(ⅰ)设样本观察值为x1,x2,…,xn,则似然函数
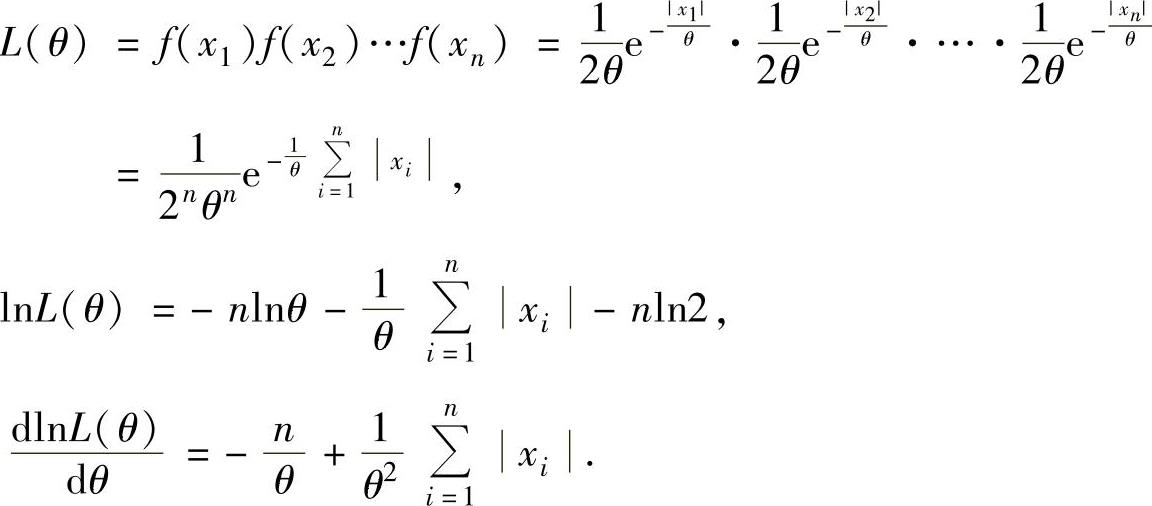
令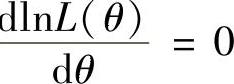 得
得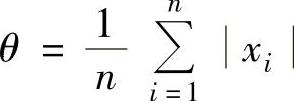 .从而θ的最大似然估计量为
.从而θ的最大似然估计量为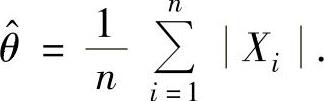
(ⅱ)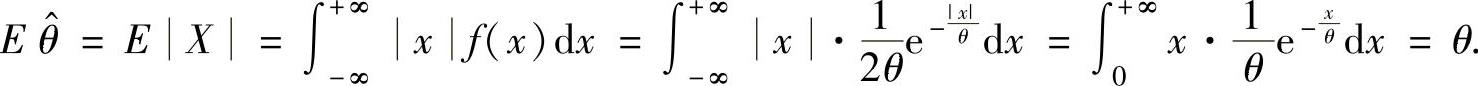
(ⅲ)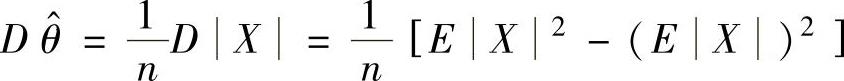
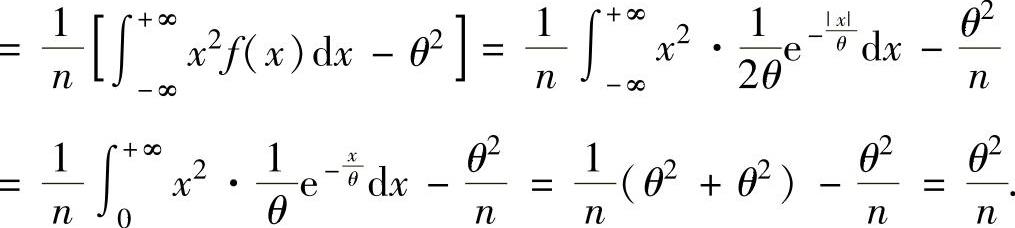
(12)θ的最大似然估计量为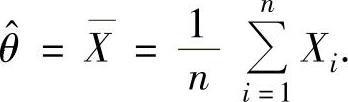 由于对任意实数x有P
由于对任意实数x有P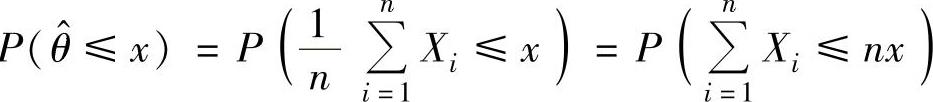 ,其中X1,X2,…,
,其中X1,X2,…,
Xn独立同分布,且数学期望为θ,方差为θ2,所以由独立同分布中心极限定理知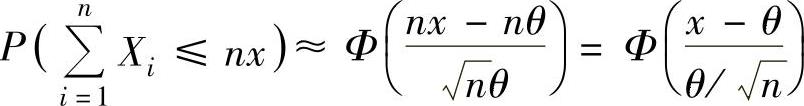 (Φ(x)是N(0,1)的分布函数).
(Φ(x)是N(0,1)的分布函数).
由此得到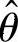 近似服从
近似服从