多元连续函数在有界闭区域上最值的计算

七 、多元连续函数在有界闭区域上最值的计算

【主要内容】

1.二元情形

设二元函数f（x，y）在有界闭区域D上连续，则它在D上必能取到最大值与最小值，当f（x，y）还在D的内部可微时，则最大值与最小值可按以下步骤计算：

（1）计算f（x，y）在D的内部的所有可能极值点，记为（x₁，y₁），（x₂，y₂），…，（x_n，y_n）.

（2）计算f（x，y）在D的边界上的最大值与最小值，分别记为M₁，m₁，其中M₁，m₁可以把边界方程代入f（x，y）转化成一元函数最值问题计算，也可以把边界方程作约束条件，用拉格朗日乘数法计算.

（3）比较f（x₁，y₁），f（x₂，y₂），…，f（x_n，y_n），M₁，m₁，其中最大者即为f（x，y）在D上的最大值，最小者即为f（x，y）在D上的最小值.

2.三元情形

设三元函数f（x，y，z）在有界闭区域Ω上连续，则它在Ω上必能取到最大值与最小值，当f（x，y，z）在Ω内部可微时，其最大值与最小值的计算方法与二元情形相同.

【典型例题】

例3.7.1求二元函数f（x，y）=x²+2y²-x²y²在闭区域D={（x，y）|x²+y²≤4，y≥0}上的最大值与最小值.

精解 先计算f（x，y）在D内部{（x，y）|x²+y²<4，y>0}的所有可能极值点.

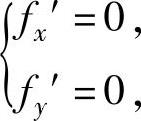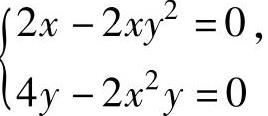解方程组即得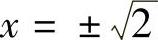，y=1，所以f（x，y）在D的内部的所有

可能极值点为，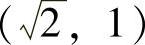

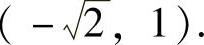
下面计算f（x，y）在D的边界C上的最值.边界C由C₁：x²+y²=4（-2≤x≤2，y≥0）和C₂：y=0（-2≤x≤2）组成.在C₁上，f（x，y）=x²+2（4-x²）-x²（4-x²），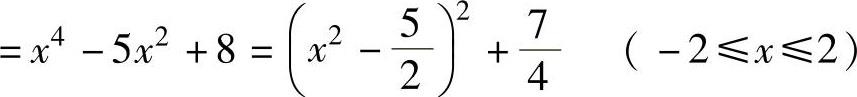

所以f（x，y）在C₁上的最大值为8（即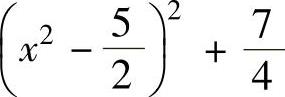在x=0处的值），最小值为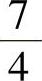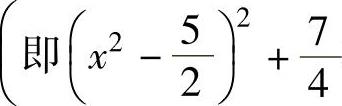在

在C₂上，f（x，y）=x²（-2≤x≤2），所以f（x，y）在C₂上的最大值为4，最小值为0.

由此可知，f（x，y）在C上的最大值为8，最小值为0.

由于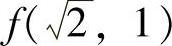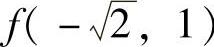，，8，0，即2，2，8，0中最大者为8，最小者为0，所以，

f（x，y）在D上的最大值为8，最小值为0.

例3.7.2 求二元函数f（x，y）=3x²+3y²-x³在有界闭区域D={（x+y）|x+y≤1，x≥0，y≥0}上的最大值与最小值.

精解 先计算f（x，y）在D内部{（x，y）|x+y<1，x>0，y>0}的可能极值点.解方程组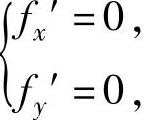即{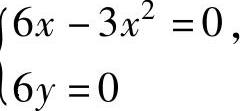得x=0，y=0；x=2，y=0，故f（x，y）的可能极值点为（0，0）和（2，0）.显然它们都不在D的内部，即在D的内部f（x，y）无可能极值点.

下面计算f（x，y）在D的边界C上的最值，显然它的最大值、最小值即为f（x，y）在D上的最大值、最小值.

边界C由三部分组成，即Ⅰ：x+y=1（0≤x≤1）；Ⅱ：y=0（0≤x≤1）；Ⅲ：x=0（0≤y≤1）.

在Ⅰ上，y=1-x，所以

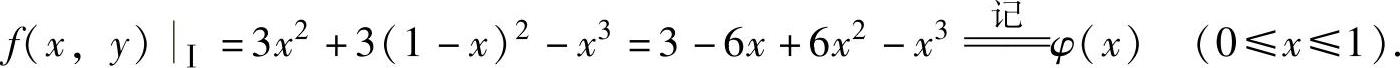
由于φ′（x）=-6+12x-3x²=-3（x²-4x+2）在（0，1）内有唯一实根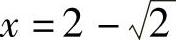，所以φ（x）

在[0，1]上的最大值为max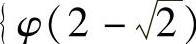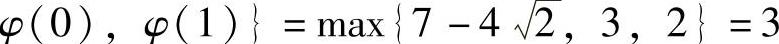，，最小值

为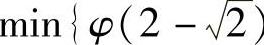，φ（0），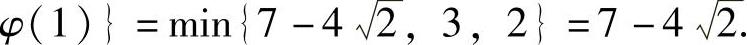

在Ⅱ上，y=0，所以(https://www.daowen.com)

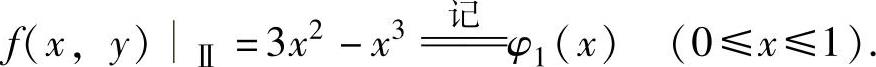
由于φ₁′（x）=6x-3x²=3x（2-x）>0（0<x<1），所以φ₁（x）在[0，1]上的最大值为φ1（1）=2，最小值为φ₁（0）=0.

在Ⅲ上，x=0，所以

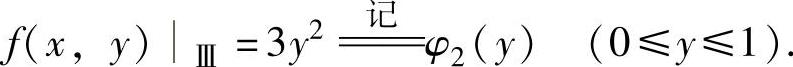
显然，φ₂（y）在[0，1]上的最大值为φ₂（1）=3，最小值为φ₂（0）=0.

综上所述，f（x，y）在C上的最大值为max{3，2，3}=3，最小值为，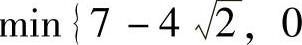

0}=0.从而f（x，y）在D上的最大值为3，最小值为0.

例3.7.3 求二元函数f（x，y）=x²+y²在闭区域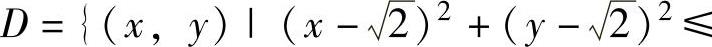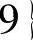上的最大值与最小值.

精解 先计算f（x，y）在D的内部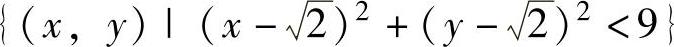的极值点.

解方程组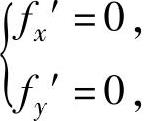即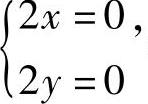得x=y=0，所以f（x，y）在D的内部有唯一的可能极值点

（0，0）.下面计算f（x，y）在D的边界C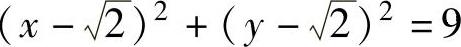：上的最值，应用拉格朗日乘

数法：记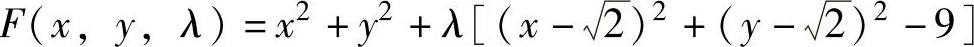，则

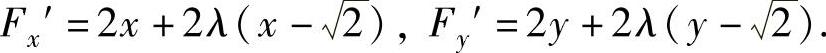
于是方程组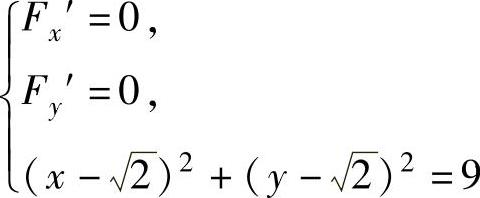

即为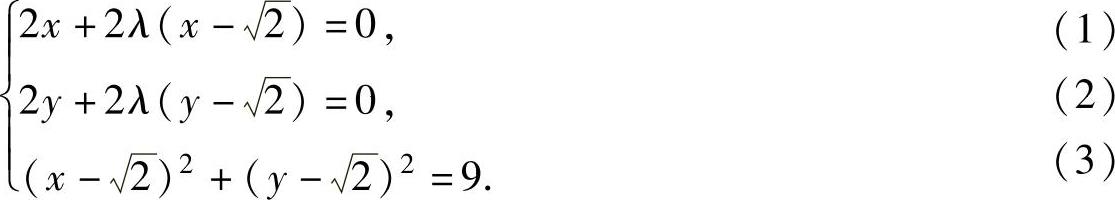

由式（1）和式（2）知x=y，将它代入式（3）得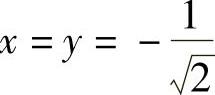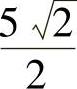，，即f（x，y）在C上有两个可

能极值点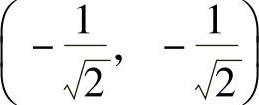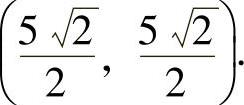，由于，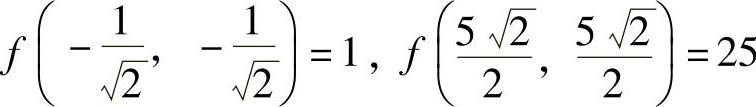

所以，f（x，y）在C上的最大值为25，最小值为1.从而f（x，y）在D上的

最大值=max{f（0，0），25}=max{0，25}=25，

最小值=min{f（0，0），1}=min{0，1}=0.

例3.7.4 求三元函数u=x²+2y²+3z²在闭区域Ω={（x，y，z）|x²+y²+z²≤100}上的最值.

精解 先计算u在Ω内部{（x，y，z）|x²+y²+z²<100}的所有可能极值点.

解方程组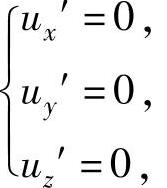即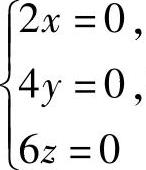得x=y=z=0，所以u在Ω内部有唯一的可能极值点（0，0，0）.

下面应用拉格朗日乘数法计算u在Ω的边界S：x²+y²+z²=100上的最值.

由于在S上u=x²+2y²+3z²=100+y²+2z²，所以，u在S上的最大值与最小值即为φ（y，z）=100+y²+2z²在yOz平面上闭区域D={（x，y）|y²+z²≤100}上的最大值与最小值.

先计算φ（y，z）在D的内部{（y，z）|y²+z²<100}的所有可能极值点.

解方程组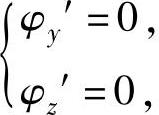即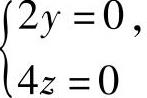得y=z=0，所以φ（y，z）在D内部有唯一可能的极值点（0，0）.

再计算φ（y，z）在D的边界C：y²+z²=100上的最值.

在C上，φ（y，z）=100+（y²+z²）+z²=200+z²（-10≤z≤10），显然它的最大值为300，最小值为200.

因此，φ（y，z）在D上的最大值=max{φ（0，0），300}=max{100，300}=300，最小值=min{100，200}=100.从而u在Ω上的最大值与最小值分别为300与0.