练习题一解答
1.单项选择题
(1)D (2)B (3)B (4)D (5)C (6)D (7)A (8)B (9)D (10)C (11)B (12)A (13)C (14)B (15)C (16)B (17)A (18)D (19)B (20)D (21)B (22)D (23)D
2.解答题
(1)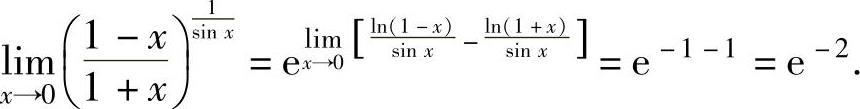
(2)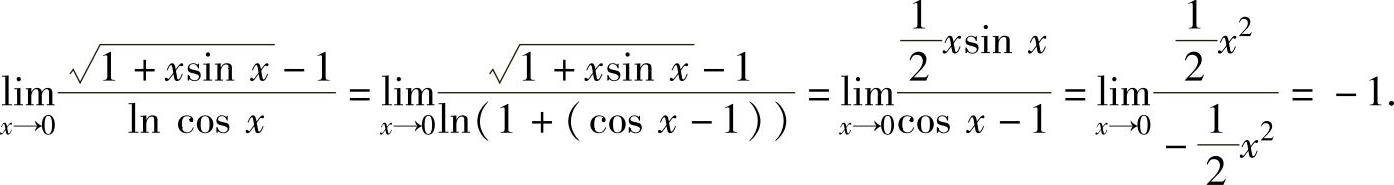
(3)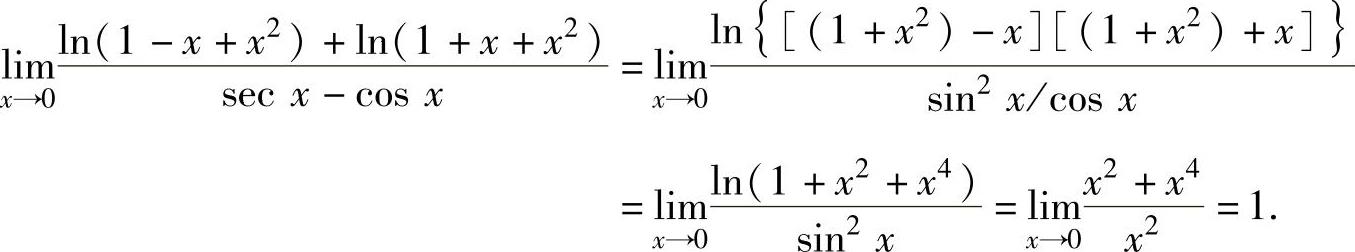
(4)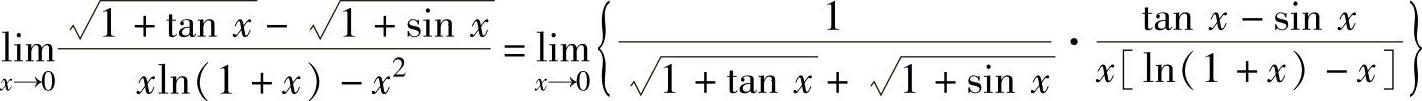
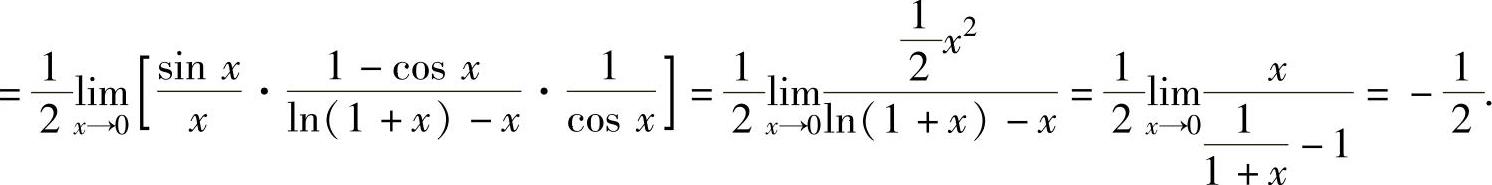
(5)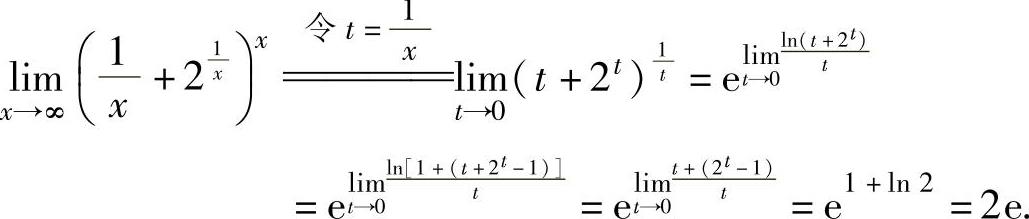
(6)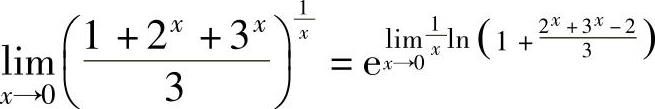
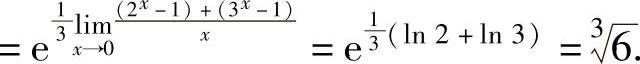
(7)由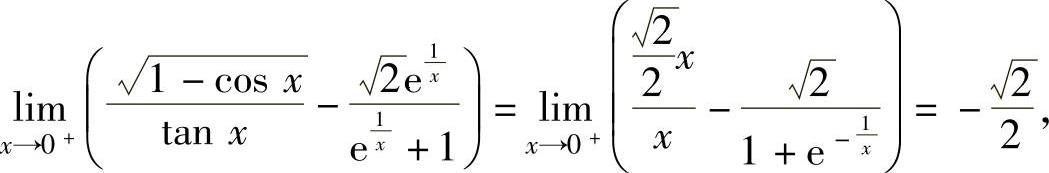
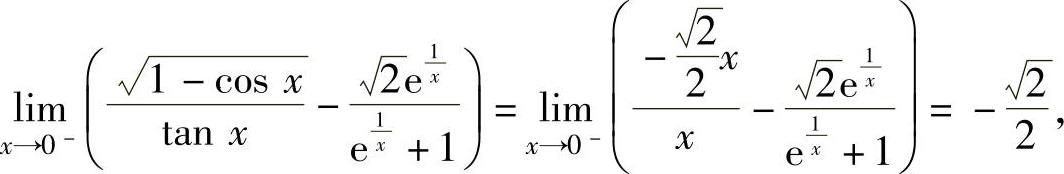
得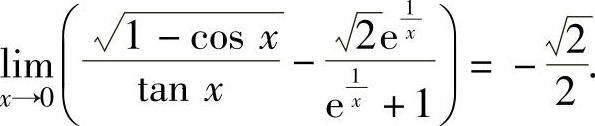
(8)由于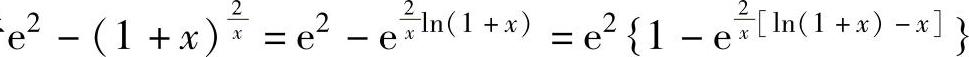
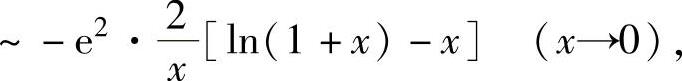
所以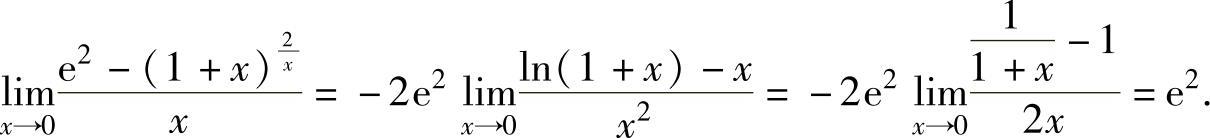
(9)由于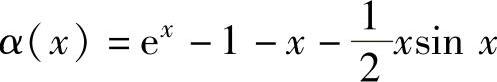
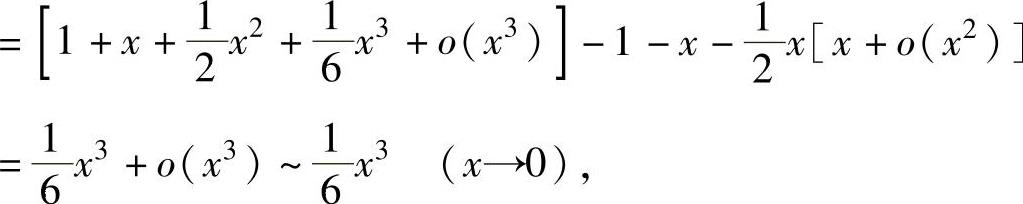
所以,x→0时,α(x)是x的三阶无穷小.
(10)记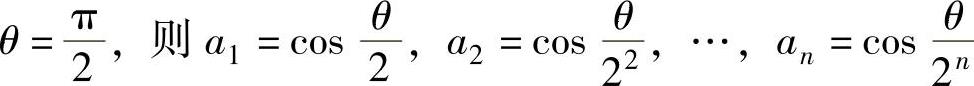 ,从而
,从而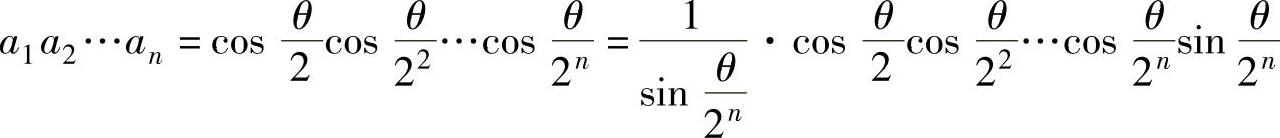
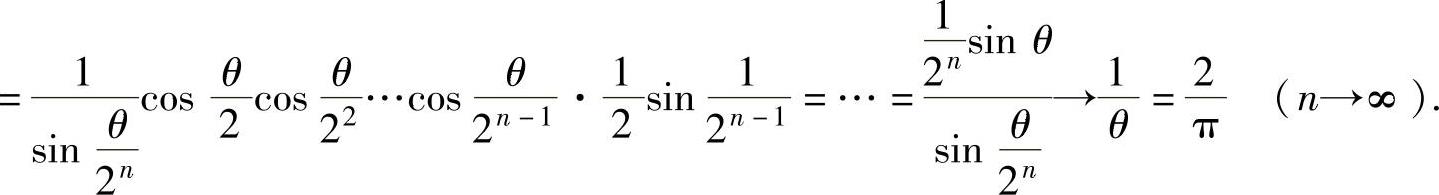
(11)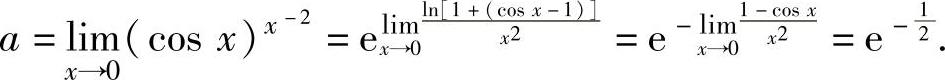
(12)由题设知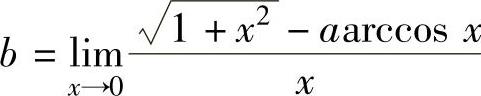 ,从而
,从而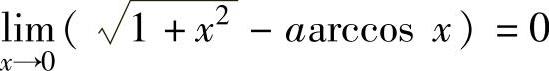 ,由此得
,由此得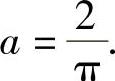 因此
因此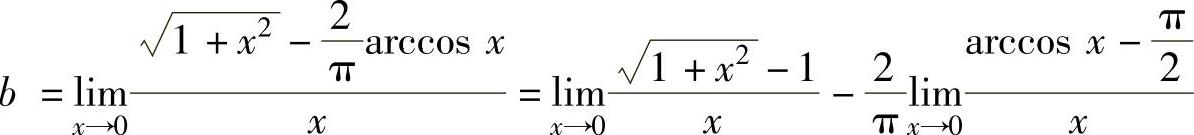
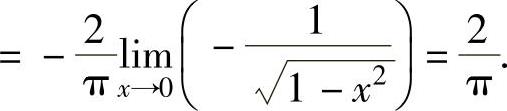
(13)x=-1是f(x)的第二类间断点(无穷间断点);
x=1是f(x)的第一类间断点(可去间断点);
x=0是f(x)的第一类间断点(跳跃间断点).
(14)记y1=xsinx,则由lny1=sinx·lnx得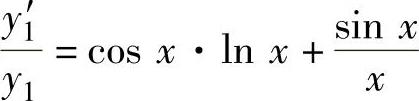 ,所以
,所以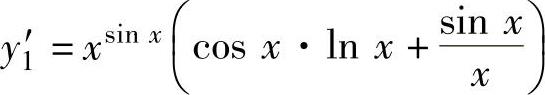 ,
,
记y2=2tan2x,则由lny2=tan2x·ln2得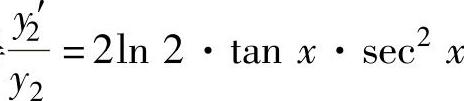 ,所以,y2′=2ln2·2tan2xtanx·sec2x.
,所以,y2′=2ln2·2tan2xtanx·sec2x.
因此,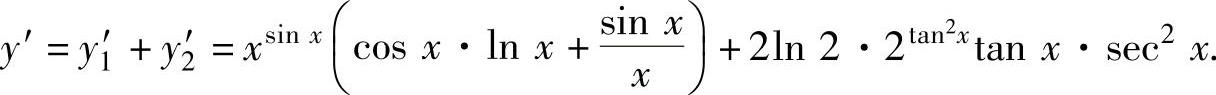
(15)y(4)=(xex·sinx)(4)=xex(sinx)(4)+C41(xex)′(sinx)‴+C42(xex)″(sinx)″+
C43(xex)‴(sinx)′+(xex)(4)sinx(https://www.daowen.com)
=xexsinx-4(x+1)excosx-6(x+2)exsinx+4(x+3)excosx+
(x+4)exsinx.
=-4(x+2)exsinx+8excosx.
(16)由于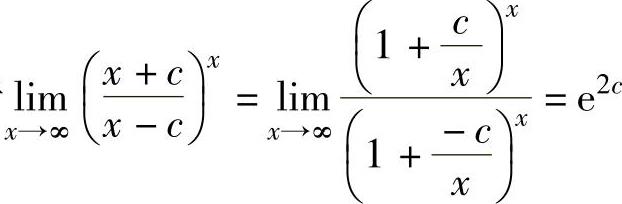 ,
,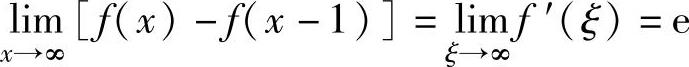 ,所以e2c=e,即
,所以e2c=e,即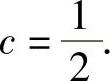
(17)f(n)(x)=(x+n)ex,f(n+1)(x)=(x+n+1)ex,f(n+2)(x)=(x+n+2)ex,由f(n+1)(x)=0得x=-n-1.所以,f(n+2)(-n-1)=e-n-1>0,所以f(n)(x)的极小值为f(n)(-n-1)=-e-n-1.
(18)x<0时,f′(x)=6(x+x2);x>0时,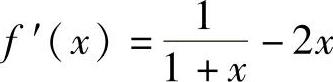 ,此外f(x)在x=0处不
,此外f(x)在x=0处不
可导.于是
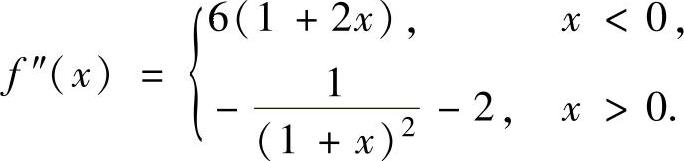
方程f″(x)=0仅有根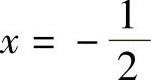 ,且当
,且当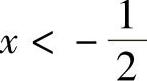 时,f″(x)<0;当
时,f″(x)<0;当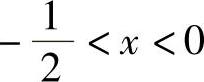 时,f″(x)>0.
时,f″(x)>0.
所以f′(x)有极小值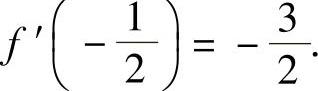
(19)记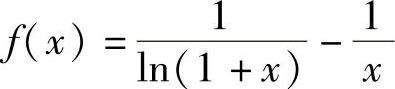 ,则它在(0,1)内可导且
,则它在(0,1)内可导且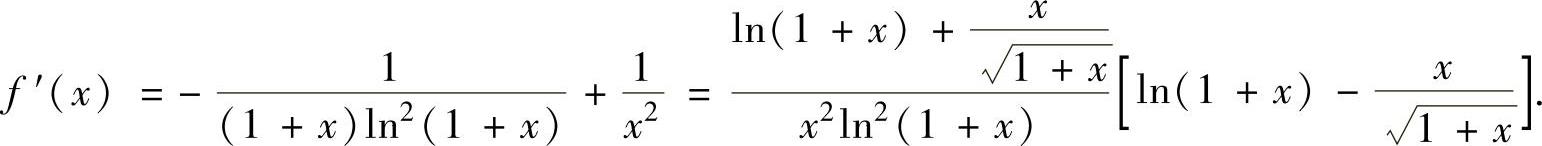
记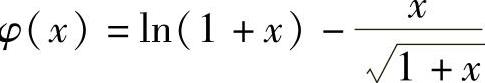 ,它在(0,1)内可导且
,它在(0,1)内可导且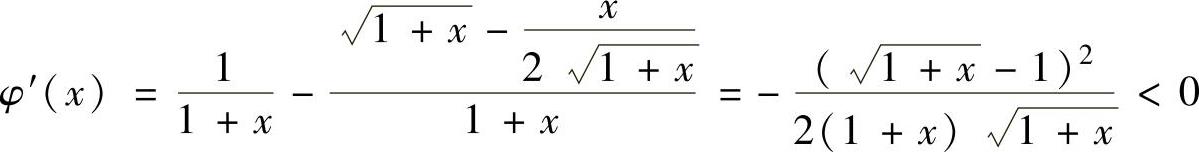 ,
,
所以,对x∈(0,1),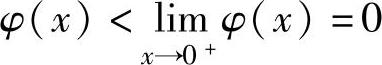 ,从而f′(x)<0.因此
,从而f′(x)<0.因此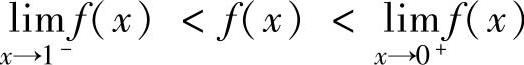 ,即
,即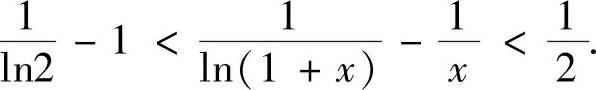
(20)记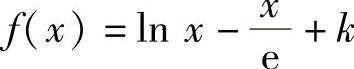 ,则它在(0,+∞)上可导且
,则它在(0,+∞)上可导且
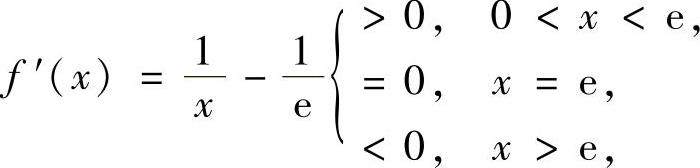
即f(x)在(0,+∞)上的最大值为k.于是,当k<0时,方程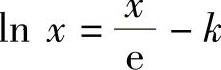 无实根;当k=0
无实根;当k=0
时,方程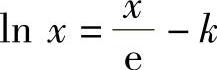 仅有一个实根;当k>0时,注意到lim
仅有一个实根;当k>0时,注意到lim
x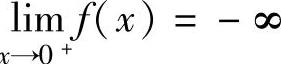 ,
,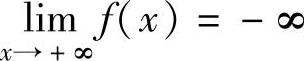
知方程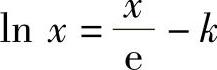 有两个实根.
有两个实根.
(21)作辅助函数F(x)=x2f(x),则F(x)在[0,1]上连续,在(0,1)内可导,且F(0)=F(1)(=0),所以,存在ξ∈(0,1),使得F′(ξ)=0,即ξf′(ξ)+2f(ξ)=0.
(22)由于bn-an=nηn-1(b-a)(η∈(a,b)).
bn-an=bnf(b)-anf(a)=[xnf(x)]′|x=ξ(b-a)
=[nξn-1f(ξ)+ξnf′(ξ)](b-a),ξ∈(a,b).
所以,nηn-1=nξn-1f(ξ)+ξnf′(ξ),即