导数的几何意义
【主要内容】
设函数f（x）在点x0处可导，则f′（x0）是曲线y=f（x）在点（x0，y0）（y0=f（x0））处切线的斜率.
曲线y=f（x）在点（x0，y0）处的切线方程为
y-y0=f′（x0）（x-x0）.
当f′（x0）≠0时，曲线y=f（x）在点（x0，y0）处的法线方程为
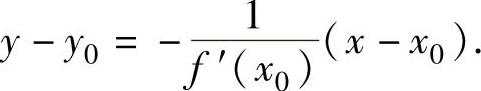
注 （ⅰ）如果f′（x0）=∞，则曲线y=f（x）在点（x0，y0）处的切线方程为x=x0；如果f′（x0）=0，则曲线y=f（x）在点（x0，y0）处的法线方程为x=x0.
（ⅱ）曲线y=f（x）在点（x0，y0）处有切线的充分必要条件是f（x）在点x0处可导或导数为∞.
【典型例题】
例1.9.1 设函数f（x）=xn（n为正整数），且曲线y=f（x）在点（1，1）处的切线与x轴交点的横坐标为ξn，求极限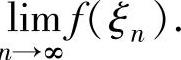
精解 算出曲线y=xn在点（1，1）处的切线方程以及ξn后即可算出极限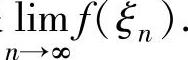
由于（xn）′x=1=n，所以曲线y=xn在点（1，1）处的切线方程为
y-1=n（x-1），（1）
它与x轴交点的横坐标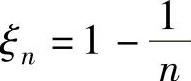
（即在式（1）中令y=0，解出的x）.
于是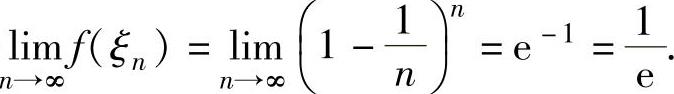
例1.9.2 设函数f（x）=（x2-x-2）x3-x，求曲线y=f（x）上不存在切线的点.
精解 首先注意：函数φ（x）=x仅在点x=0处不可导，即φ′（0）不存在，但不为∞；函数xx处处可导.
于是，f（x）=（x2-x-2）x3-x=[（x-2）（x+1）x+1]xx-1仅在点x=0，1两点处不可导，即f′（0），f′（1）都不存在，但都不为∞.所以曲线y=f（x）仅在点（0，0）和点（1，0）处不存在切线.
例1.9.3 设周期为4的周期函数f（x）在（-∞，+∞）上可导，且lim
x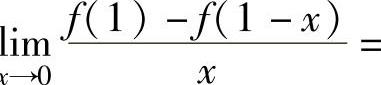
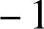
，求曲线在点（5，f（5））处的法线斜率.
精解 由于法线斜率为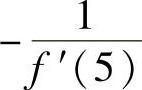
，所以只要算出f′（5）即可.
由
可知，曲线y=f（x）在点（5，f（5））的法线斜率为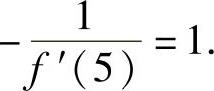
例1.9.4 设曲线C：y=x3-3x2+5的切线l与直线x+9y=1垂直，求l的方程.
精解 设切点为（x0，y0）（其中y0=x30-3x20+5），只要算出x0，就可确定l的方程.由于（x0，y0）满足
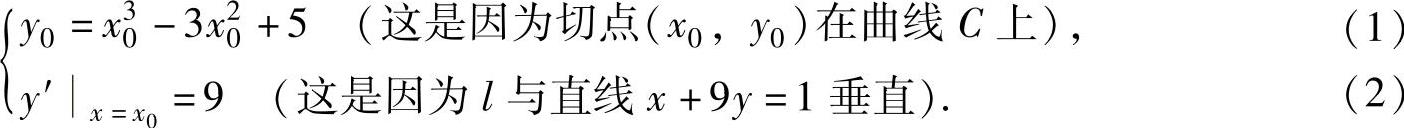
由式（2）得 x20-2x0-3=0，即x0=-1，3.将它代入式（1）对应得y0=1，5.所以l的方程为
y-1=9（x+1）及y-5=9（x-3），即y=9x+10及y=9x-22.
注 计算曲线y=f（x）的切线方程时，如果未知切点坐标，则总是设切点坐标为（x0，f（x0）），然后计算x0.
例1.9.5 设两曲线y=x2+ax+b，2y=-1+xy3相切于点（1，-1），求常数a，b及公切线.
精解 由于两曲线相切于点（1，-1），所以a，b应满足
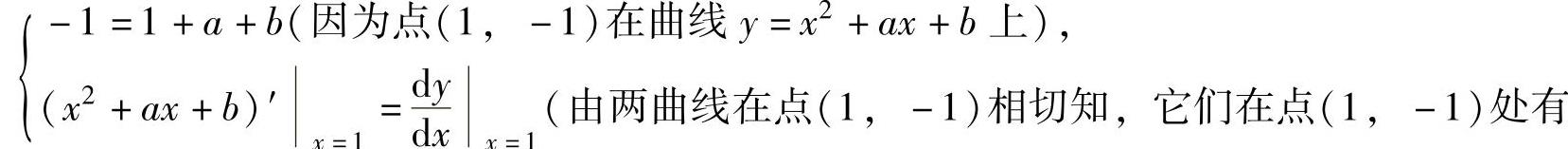
相同的切线斜率，其中，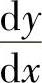
是方程2y=-1+xy3两边对x求导所得）
其中，（x2+ax+b）′x=1=2+a，此外，方程2y=-1+xy3两边对x求导得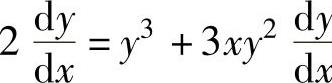
y，即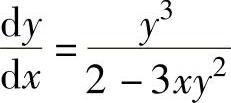
，
所以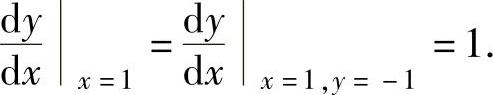
将它们代入上面所列方程组得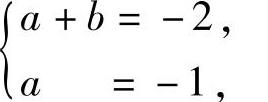
即 a=b=-1.
并且公切线方程为
y+1=1·（x-1）， 即 y=x-2.