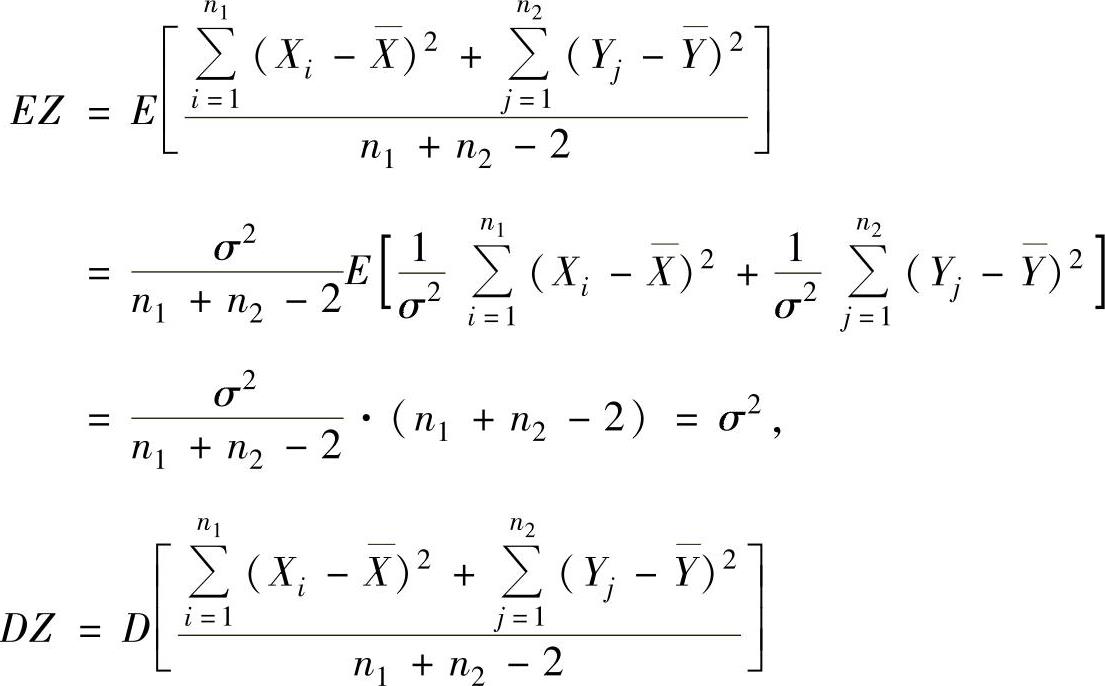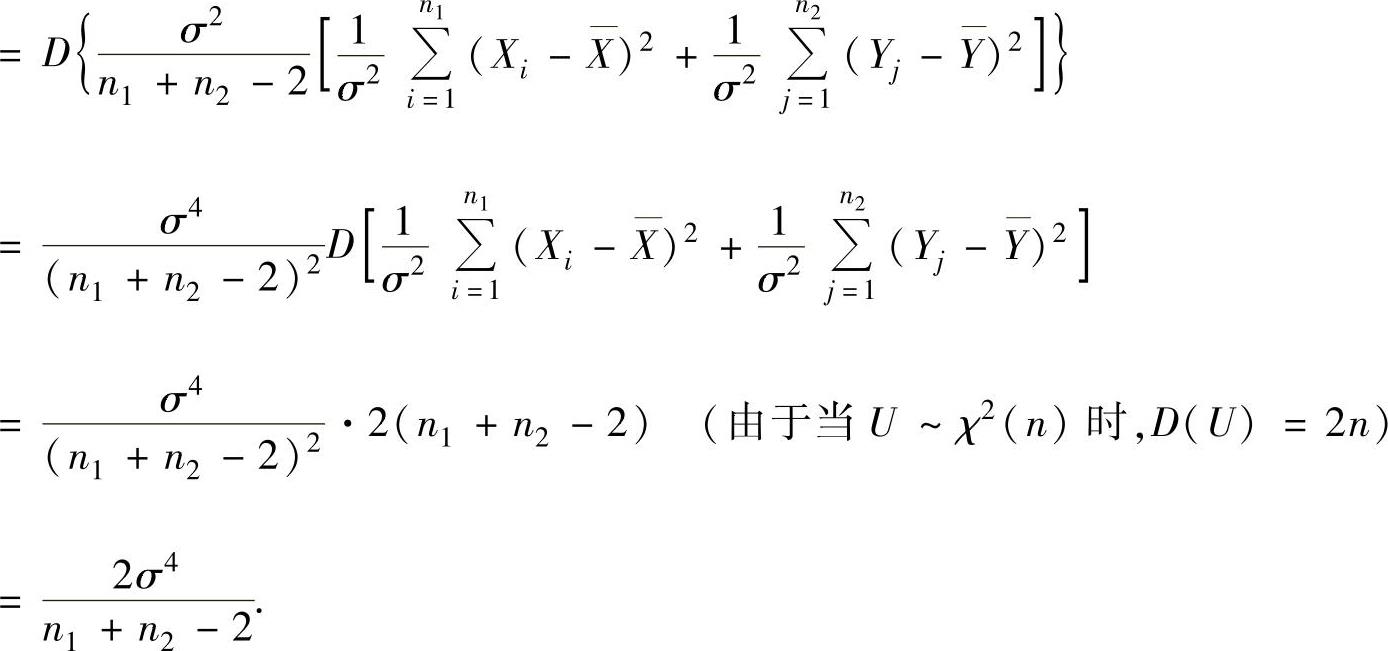正态总体样本的常用统计量及其分布
【主要内容】
1.一个正态总体情形
设总体X~N(μ,σ2)(此时简称X是正态总体),X1,X2,…,Xn是来自X的一个简单随机样本,其均值为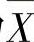 ,方差为S2,则有关统计量及其分布如下:
,方差为S2,则有关统计量及其分布如下:
(1)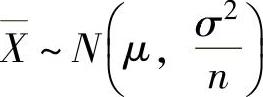 ,即
,即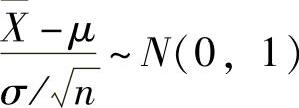 ,并且
,并且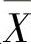 与S2相互独立.
与S2相互独立.
(2)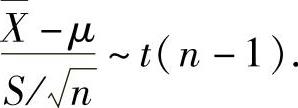
(3)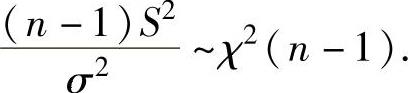
2.两个正态总体情形
设总体X~N(μ1,σ12),Y~N(μ2,σ22),它们相互独立.X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自总体X和Y的简单随机样本,它们的均值分别为X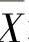 和
和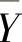 ,方差分别为S12和S22,则有关统计量及其分布如下:
,方差分别为S12和S22,则有关统计量及其分布如下:
(1)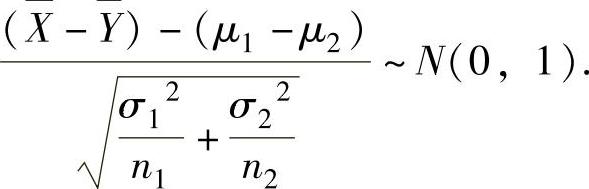
(2)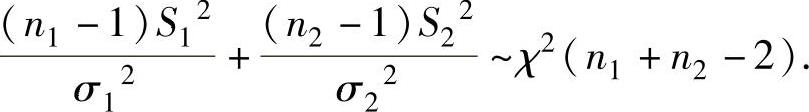
(3)当σ1=σ2时,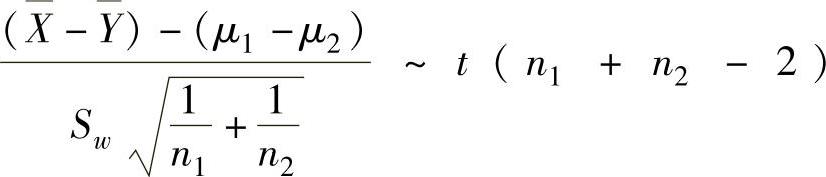 ,其中Sw2=
,其中Sw2=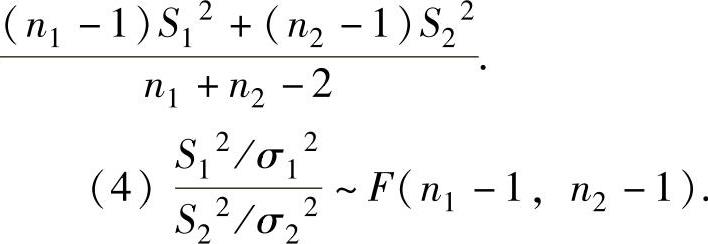
【典型例题】
例8.2.1 (单项选择题)设X1,X2,…,X9是来自总体X~N(μ,σ2)的简单随机样本.记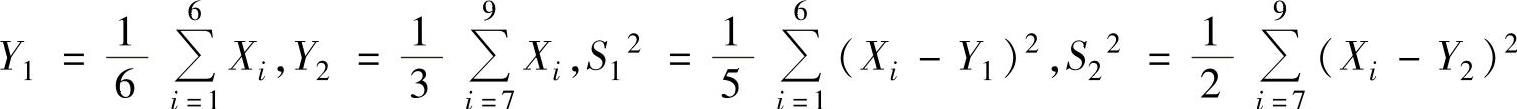 ,则随机变量
,则随机变量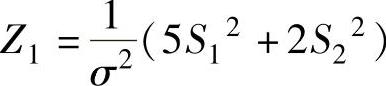 ,
,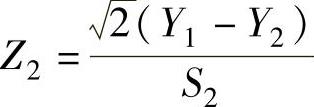 分别服从( ).A.χ2(9),t(2)B.χ2(7),t(3)C.χ2(7),t(2)D.χ2(9),t(3)
分别服从( ).A.χ2(9),t(2)B.χ2(7),t(3)C.χ2(7),t(2)D.χ2(9),t(3)
精解 先考虑Z1.
由于随机变量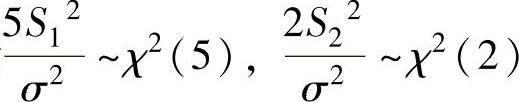 ,且它们相互独立,所以由χ2分布的性质得
,且它们相互独立,所以由χ2分布的性质得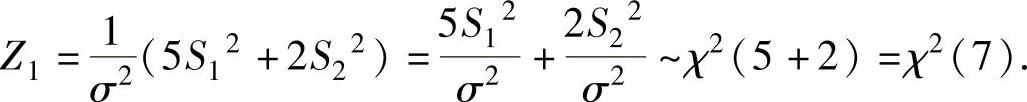
下面考虑Z2.(https://www.daowen.com)
由随机变量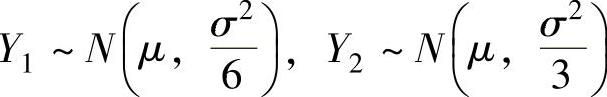 ,且它们相互独立知
,且它们相互独立知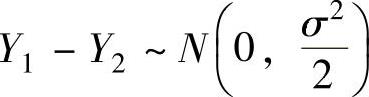 ,
,
所以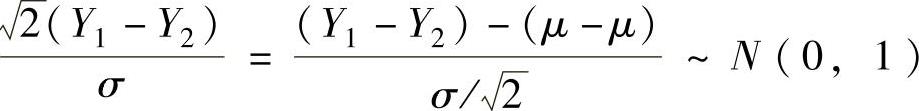 .由上已知
.由上已知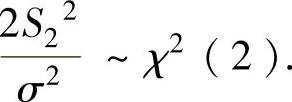 此外,
此外,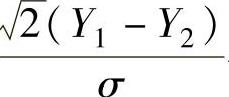 与
与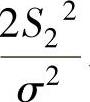 相互独立(这是由于Y1与S22相互独立,Y2与S22相互独立,所以
相互独立(这是由于Y1与S22相互独立,Y2与S22相互独立,所以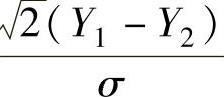 与
与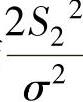 相互独立),所以由t分布的定义得
相互独立),所以由t分布的定义得
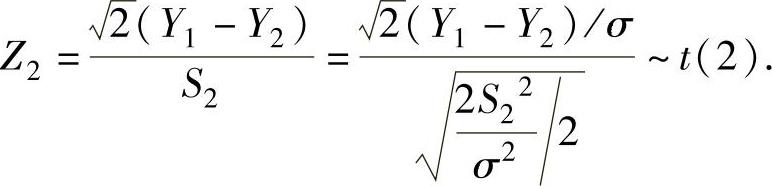
因此本题选C.
例8.2.2 设X1,X2,X3,X4是来自正态总体X~N(0,22)的简单随机样本.记Z=a(X1-2X2)2+b(3X3-4X4)2,求参数a,b(a>0,b>0)的值,使得Z服从χ2分布,并求这个χ2分布的自由度.
精解 记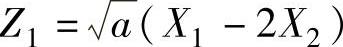 ,
,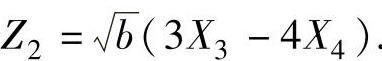 要使Z服从χ2分布,必须使Z1,
要使Z服从χ2分布,必须使Z1,
Z2~N(0,1),从而a,b应满足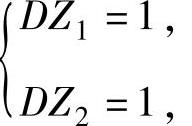 即
即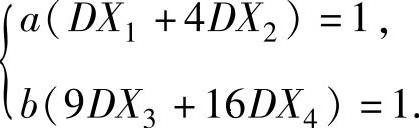
由此得到a(4+4×4)=1,即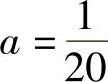 ;b(9×4+16×4)=1,即
;b(9×4+16×4)=1,即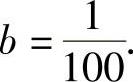
此时,Z=Z12+Z22,其中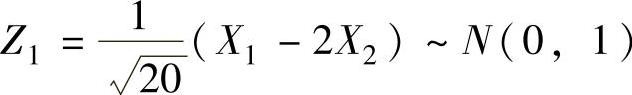 ,
,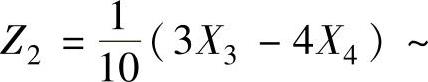 N(0,1),且Z1与Z2相互独立,所以Z服从自由度为2的χ2分布.
N(0,1),且Z1与Z2相互独立,所以Z服从自由度为2的χ2分布.
例8.2.3 设X1,X2是来自总体X~N(0,1)的一个简单随机样本.
(1)证明:随机变量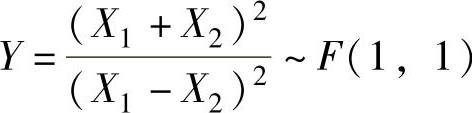 ,并求概率P(Y≤39.86);
,并求概率P(Y≤39.86);
(2)已知概率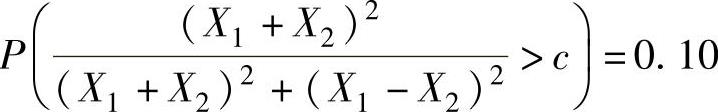 ,求常数c.
,求常数c.
精解 (1)记Y1=X1+X2,Y2=X1-X2,则Y1,Y2都服从N(0,2),所以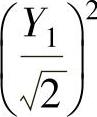 和
和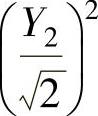 都服从χ2(1).
都服从χ2(1).
此外,由Cov(Y1,Y2)=Cov(X1+X2,X1-X2)=Cov(X1,X1)-Cov(X2,X2)=DX1-DX2=1-1=0
知Y1与Y2相互独立,即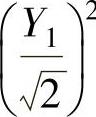 与
与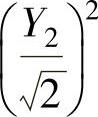 相互独立.于是由F分布的定义得证
相互独立.于是由F分布的定义得证
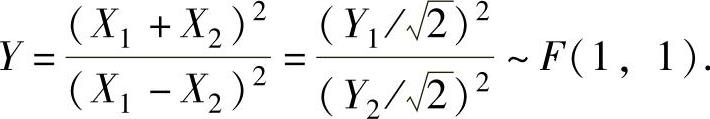
查表
由此可得P(Y≤39.86)=1-P(Y>39.86)1-0.10=0.90.
(2)由于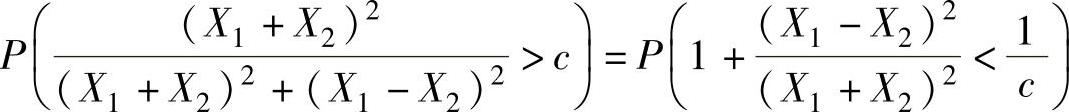
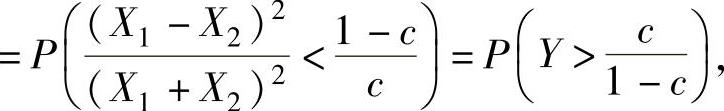
所以由题设得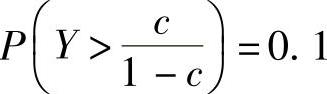 ,查F(1,1)分布表得
,查F(1,1)分布表得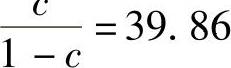 ,所以c=0.97.
,所以c=0.97.
例8.2.4 设总体X~N(μ1,σ2),Y~N(μ2,σ2),它们相互独立.又设X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自X和Y的简单随机样本,记
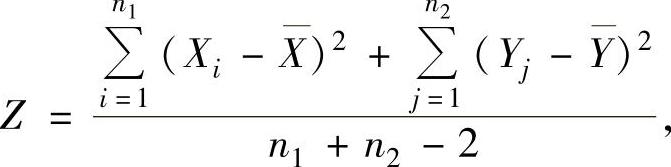
求EZ和DZ.
精解 由两个正态情形的样本统计量的分布知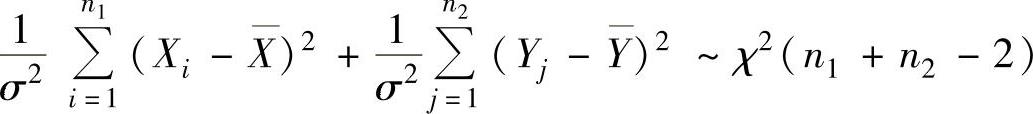 ,
,
所以