六、矩阵的秩
【主要内容】
1.矩阵秩的定义
设A是m×n矩阵,则称A的不为零的子行列式(简称子式)的最高阶数为A的秩,记为r(A),其中,A的k(k≤min{m,n})阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.
零矩阵的秩定义为0.
2.矩阵秩的性质
(1)设A是m×n矩阵,则0≤r(A)≤min{m,n}.
(2)设A是m×n矩阵,k是常数,则
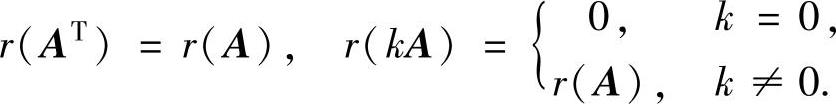
(3)初等变换不改变矩阵的秩,即等价矩阵的秩相等.
(4)设A,B都是m×n矩阵,则r(A+B)≤r(A)+r(B).
(5)设A,B分别是m×s,s×n矩阵,则r(A)+r(B)-s≤r(AB)≤min{r(A),r(B)}.
(6)设A是n阶矩阵,则A可逆的充分必要条件是r(A)=n.
(7)分块矩阵

的秩都为r(A)+r(B).
3.矩阵秩的计算
通常,用以下的初等行变换方法计算矩阵的秩:
设A是m×n矩阵,经过一系列初等行变换后成为阶梯形矩阵B,则r(A)等于B中非零行的个数,其中,满足以下条件的矩阵称为阶梯形矩阵:
(1)元素全为零的行(称为零行)在矩阵的最下方.
(2)对于非零行,第i+1行的由左至右的第一个非零元素的列标必大于第i行由左至右的第一个非零元素的列标.例如
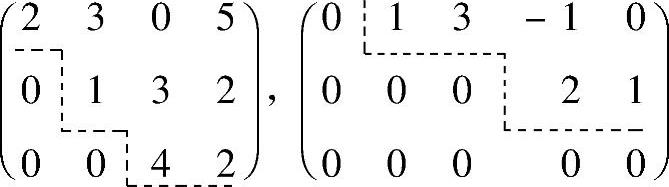
都是阶梯形矩阵.
【典型例题】
例5.6.1 (单项选择题)设A是m×n矩阵,B是n×m矩阵,则( ).
A.当m>n时,|AB|≠0 B.当m>n时,|AB|=0
C.当m<n时,|AB|≠0 D.当m<n时,|AB|=0
精解 显然,AB是m阶矩阵.由r(AB)≤min{m,n}知,当m>n时有r(AB)≤n<m,即AB的秩小于它的阶数,所以|AB|=0.
因此本题选B.
例5.6.2 已知
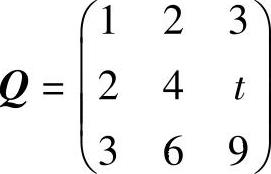
,P为三阶非零矩阵,且PQ=O3,则( ).
A.t=6时,P的秩必为1 B.t=6时,P的秩必为2(https://www.daowen.com)
C.t≠6时,P的秩必为1 D.t≠6时,P的秩必为2
精解 当t≠6时,由
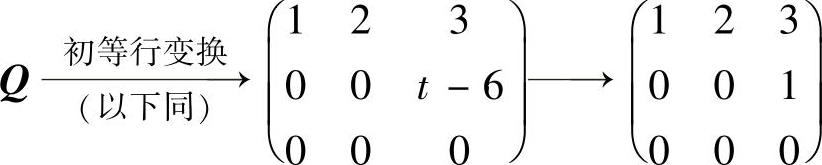
知r(Q)=2.
此外,由PQ=O3知r(P)+r(Q)-3≤r(PQ)=0,即0<r(P)≤1(利用P是非零矩阵和r(Q)=2).由此得到r(P)=1.
因此本题选C.
例5.6.3 求矩阵A的秩,其中
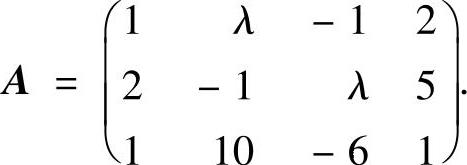
精解 利用初等行变换法计算A的秩.
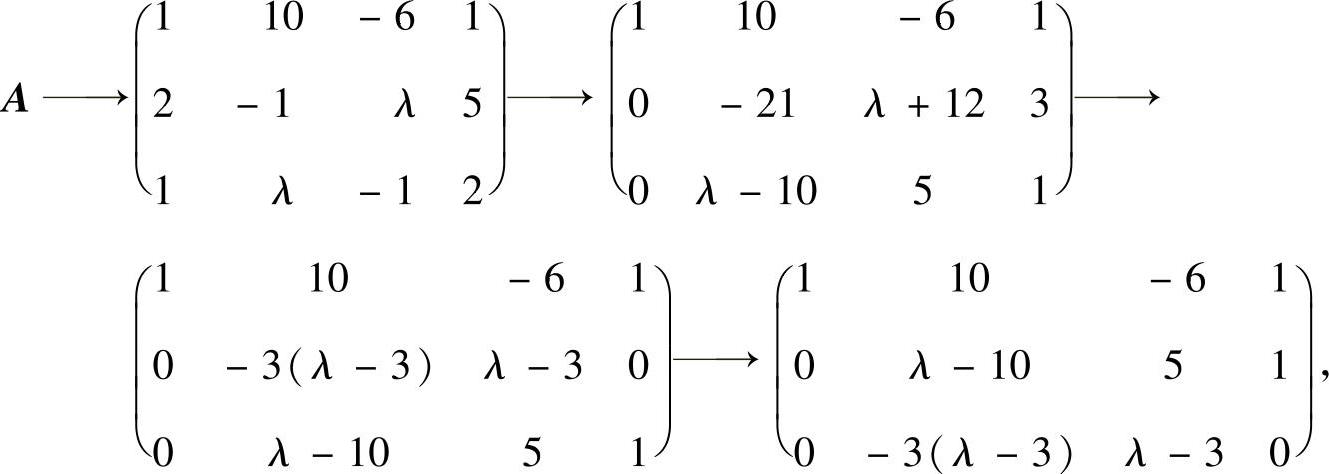
所以,当λ-3=0,即λ=3时,由
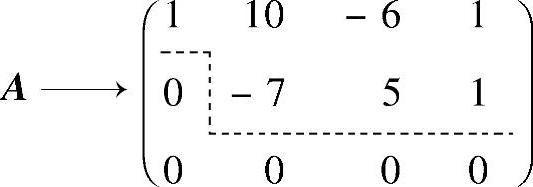
知r(A)=2.此外,当λ≠3时,由
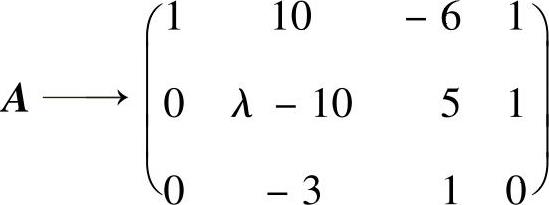
知 r(A)=3(这是因为
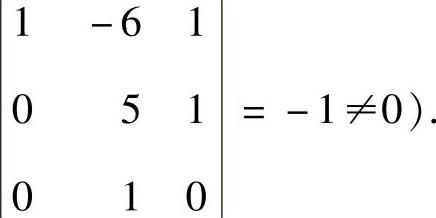
例5.6.4 设矩阵
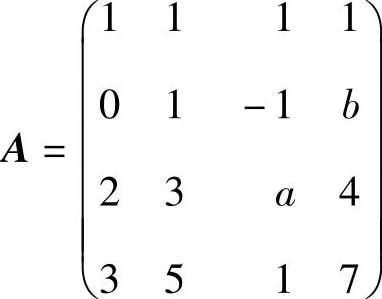
的秩为3,求a,b的取值范围.
精解 用初等行变换法将A化为阶梯形矩阵,然后根据r(A)=3,确定a,b的值.

于是,由r(A)=3知,a,b应满足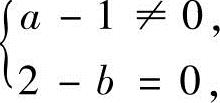 或
或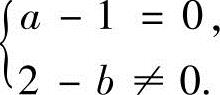
所以,取值范围是a≠1且b=2,或a=1且b≠2.
例5.6.5 设A,B都是n阶矩阵,且ABA=B-1.证明:
r(En+AB)+r(En-AB)=n.
精解 利用矩阵秩的性质证明
r(En+AB)+r(En-AB)≤n和r(En+AB)+r(En-AB)≥n同时成立即可.
由ABA=B-1得ABAB=En,所以
(En+AB)(En-AB)=En+AB-AB-ABAB=On.从而有
r(En+AB)+r(En-AB)-n≤r((En+AB)(En-AB))=0,即r(En+AB)+r(En-AB)≤n.(1)
此外,r(En+AB)+r(En-AB)≥r((En+AB)+(En-AB))=r(2En)=n,即r(En+AB)+r(En-AB)≥n.(2)
由式(1)和式(2)得
r(En+AB)+r(En-AB)=n.
