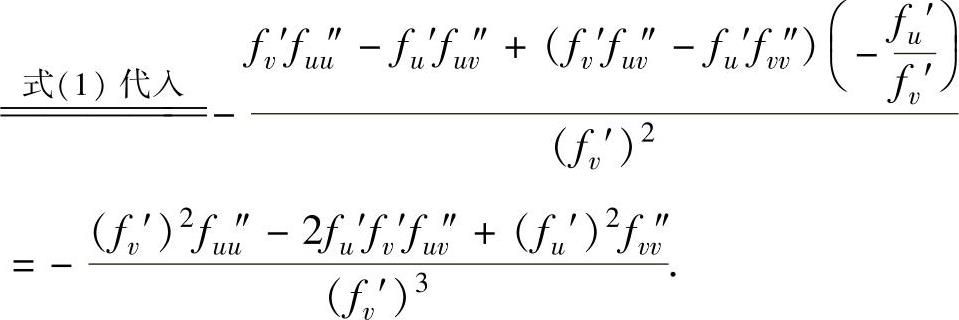二元隐函数偏导数及二阶偏导数的计算

四 、二元隐函数偏导数及二阶偏导数的计算

【主要内容】

1.二元隐函数偏导数的计算

设二元函数z=z（x，y）由方程F（x，y，z）=0确定，则称z=z（x，y）是二元隐函数.它的偏导数可按以下步骤计算：

（1）所给方程两边对x（或y）求偏导数（此时应注意z是关于x与y的二元函数）得；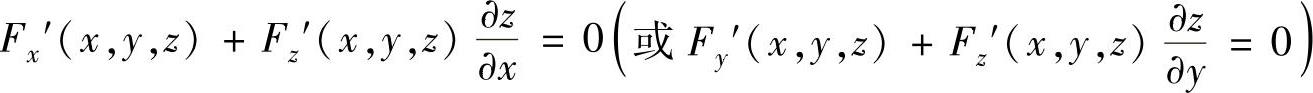

（2）解上述以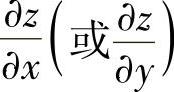为未知数的方程，即得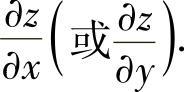

注 关于方程F（x，y，z）=0确定隐函数z=z（x，y）有以下的隐函数定理：

设F（x，y，z）在点（x₀，y₀，z₀）的某个邻域内有连续偏导数，并且F（x₀，y₀，z₀）=0，F_z′（x₀，y₀，z0）≠0，则方程F（x，y，z）=0在点（x₀，y₀，z₀）的某个邻域内确定唯一的具有连续偏导数的函数z=z（x，y），它还满足z₀=z（x₀，y₀）及F（x，y，z（x，y））≡0.

2.二元隐函数二阶偏导数的计算

二元隐函数的二阶偏导数，可以对已求得的一阶偏导数再求偏导数得到.(https://www.daowen.com)

【典型例题】

例3.4.1 设二元函数z=z（x，y）由方程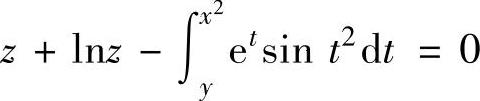确定，求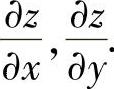

精解 所给方程两边求全微分得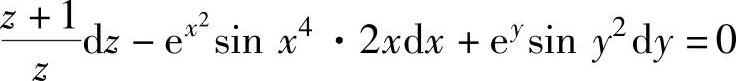

即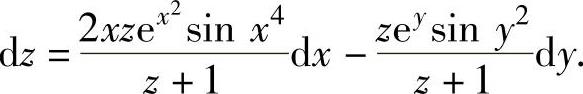

所以，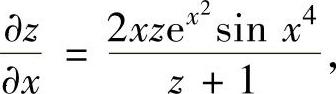

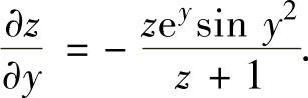
注 由于本题需计算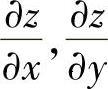，所以不是从对所给方程两边分别求关于x和关于y的偏导数入手，而是从对所给方程两边求全微分入手.

例3.4.2 设二元函数z=z（x，y）由方程f（x+y，y+z）=0确定，其中，函数f（u，v）具有二阶连续偏导数，且f_v′≠0.求z_x″_x.

精解 由二元隐函数求偏导数方法先算出z_x′，然后计z_x″_x.

记u=x+y，v=y+z，在所给方程两边对x求偏导数得f_u′+f_v′z_x′=0， 即

于是，