三、矩阵方程求解

三 、矩阵方程求解

【主要内容】

设A是m×n矩阵，B是m×l矩阵，它们都是已知矩阵，X是未知矩阵，则称方程AX=B为矩阵方程.满足AX=B的矩阵X称为该方程的解.

设A=（A┆B），称为该矩阵方程的增广矩阵，则

AX=B有唯一解的充分必要条件是，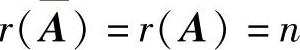

AX=B有无穷多解的充分必要条件是，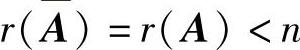

AX=B无解的充分必要条件是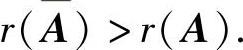

注 （ⅰ）矩阵方程AX=O（其中，A是已知的m×n矩阵，O是m×l零矩阵）有非零解的充分必要条件是r（A）<n（只有零解的充分必要条件是r（A）=n）.

（ⅱ）当A是n阶可逆矩阵时，矩阵方程AX=B的唯一解为

X=A^-1B.

（ⅲ）当矩阵方程AX=B有无穷多解时，其解的一般表达式称为通解或一般解.

【典型例题】

例6.3.1 设三阶矩阵

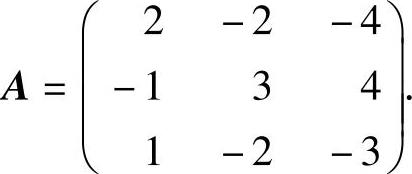
（1）证明：存在三阶矩阵B（B≠E₃），使得AB=A；

（2）求出所有满足AB=A的矩阵B（B≠E₃）.

精解 本题实际是证明矩阵方程AX=O₃有解，并求其通解.

（1）由于

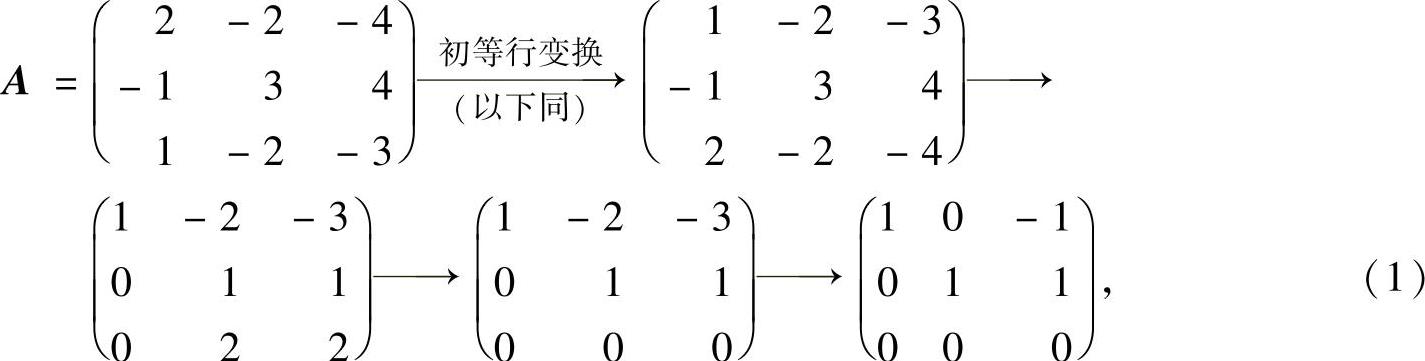
所以 r（A）=2<3，因此矩阵方程AX=O有非零解，即存在非零矩阵B-E₃使得A（B_- E₃）=O₃.由此证得存在三阶不为E₃的矩阵B，使得

AB=A.

（2）记矩阵方程AX=O₃的解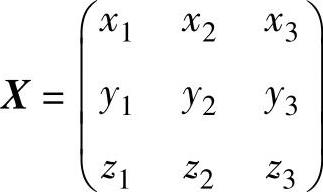，则由（1）知AX=O₃与矩阵方程

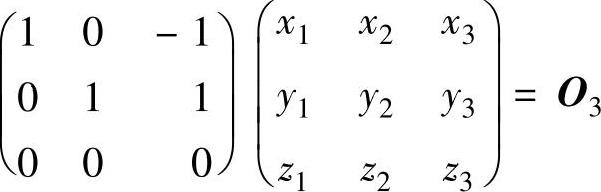
同解.

显然（x_i，y_i，zi）（i=1，2，3）都是方程组

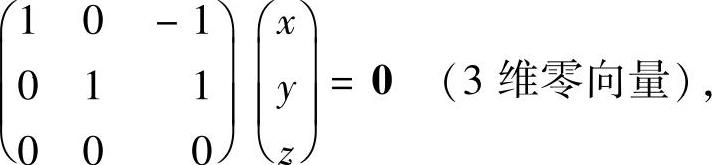(https://www.daowen.com)

即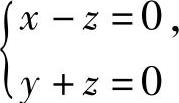

的解，而该方程组的通解为c（1，-1，1）T=（c，-c，c）T.因此

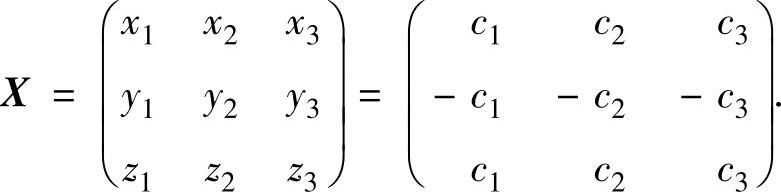
由于B≠E₃，所以所求的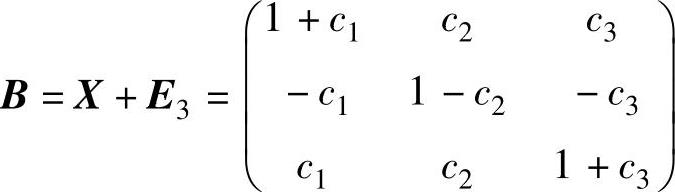（其中，c₁，c₂，c3是不

全为零的任意常数）.

例6.3.2 设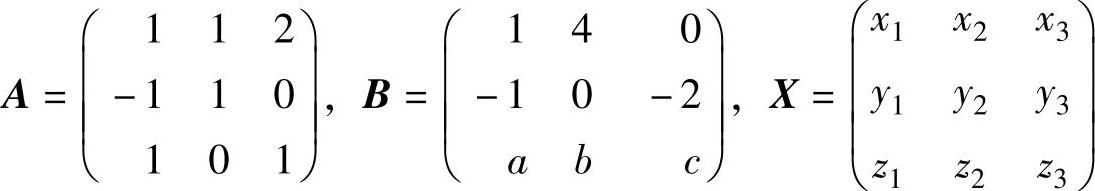，问a，b，c取

何值时，矩阵方程AX=B有无穷多解？并求出此时矩阵方程的通解.

精解 对所给矩阵方程AX=B的增广矩阵（A┆B）施行初等行变换：

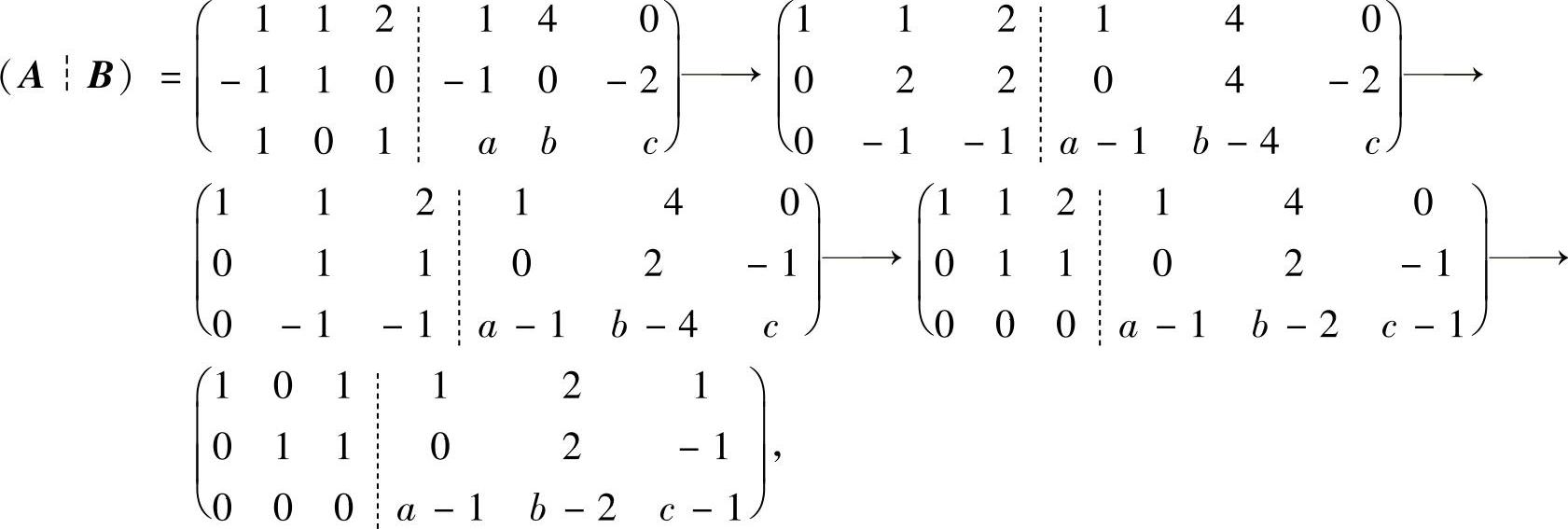
由此可知，当a-1=b-2=c-1=0，即a=1，b=2，c=1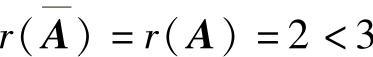时，，此时

矩阵方程AX=B有无穷多解.由于此时AX=B与矩阵方程

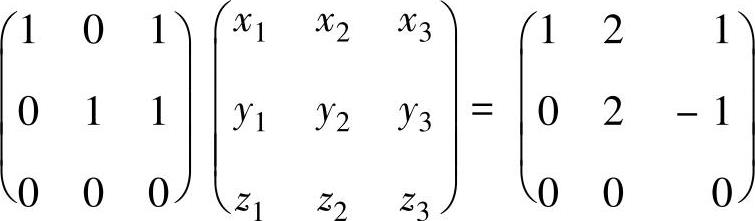
同解，而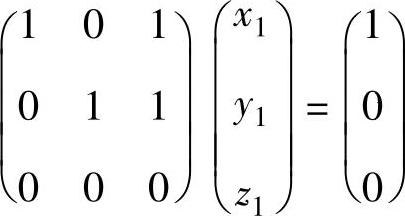的通解为（x₁，y₁，z₁）T=c₁（-1，-1，1）T+（1，0，0）T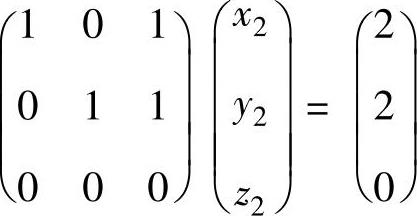，的通解为（x₂，y₂，z₂）T=c₂（-1，-1，1）T+（2，2，0）T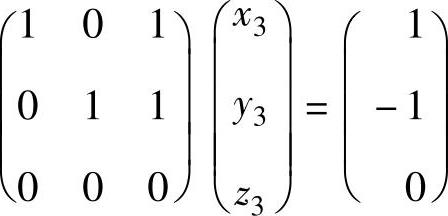，的通解为（x₃，y₃，z₃）T=c₃（-1，-1，1）T+（1，-1，0）T.

所以，所求的通解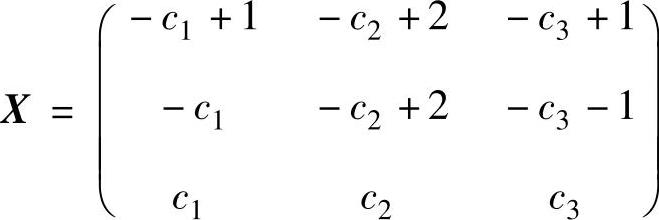（其中，c₁，c₂，c3都是任意常数）.

例6.3.3 已知向量组

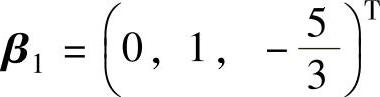
，β₂=（a，2，1）^T，β₃=（b，1，0）^T可由向量组α₁=（1，2，-3）^T，α₂=（3，0，c）^T，α₃=（9，6，-7）^T线性表示，而且表达式并不是唯一的，求a，b，c的值.

精解 将向量组的线性表达式转换成矩阵方程，然后利用表达式不是唯一，即该矩阵方程有无穷多解，由此确定a，b，c的值.

设向量组β₁，β₂，β³由向量组α₁，α₂，α₃的线性表达式为

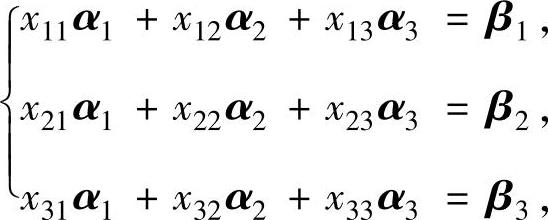
即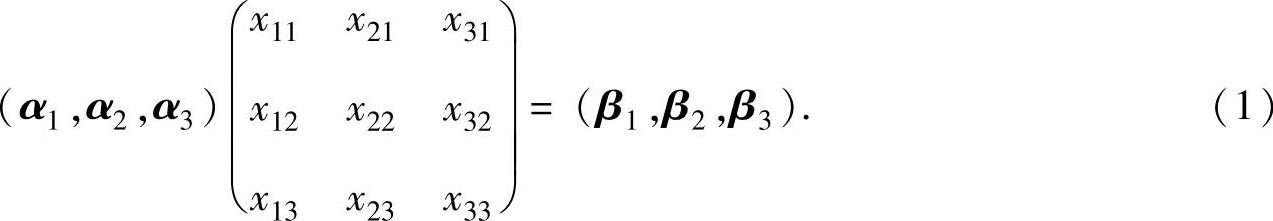

对矩阵方程（1）的增广矩阵（α₁，α₂，α₃┆β₁，β₂，β₃）施行初等行变换

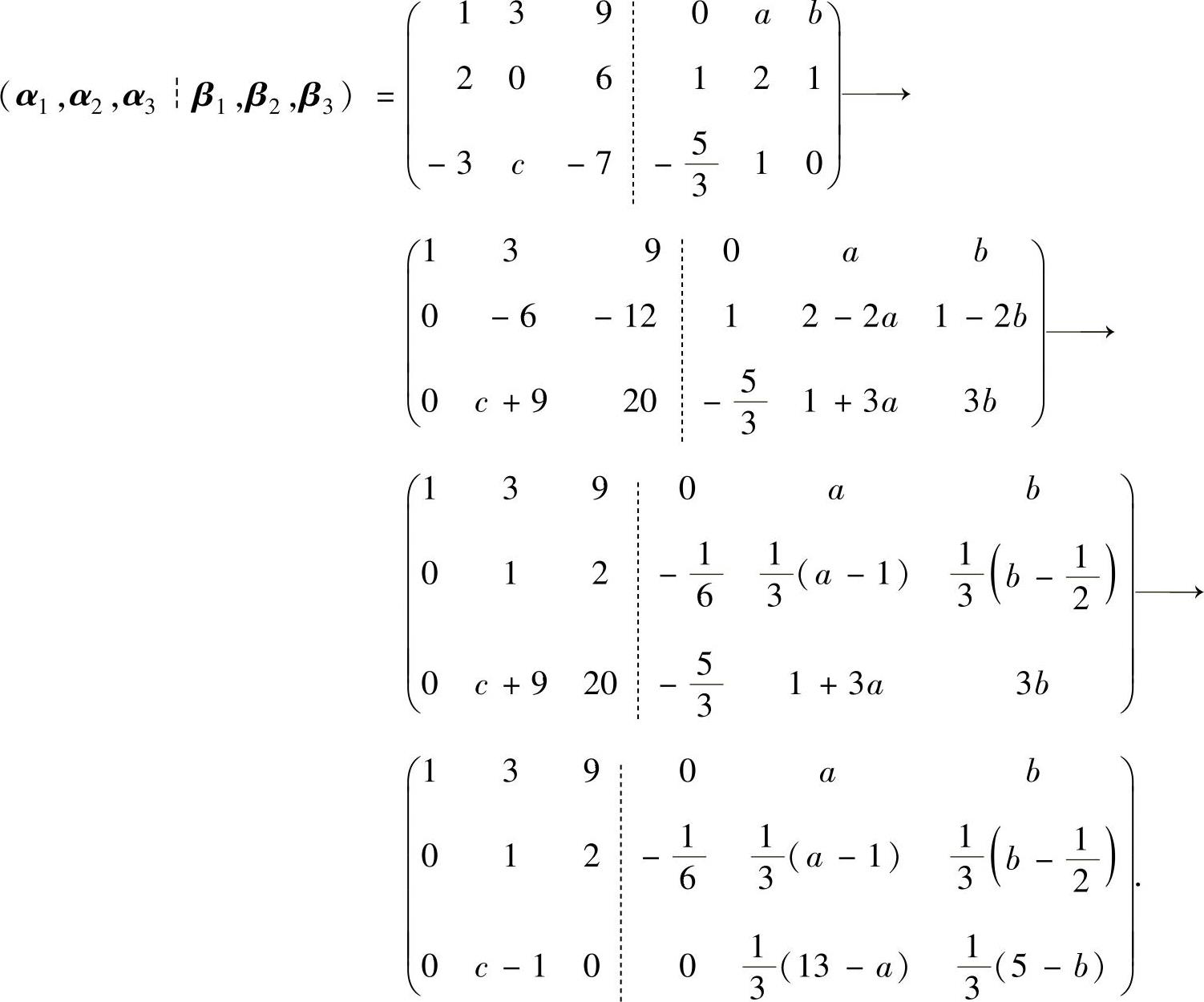
由题设知矩阵方程（1）有无穷多解，所以

r（α₁，α₂，α₃┆β₁，β₂，β₃）=r（α₁，α₂，α₃）=2.

由此得到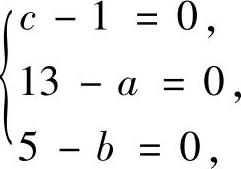即a=13，b=5，c=1.