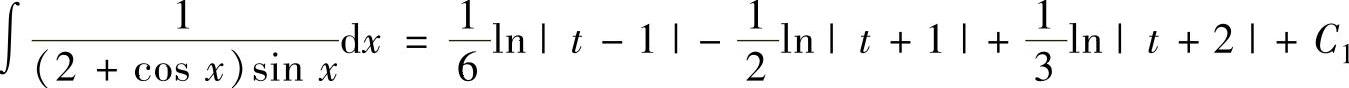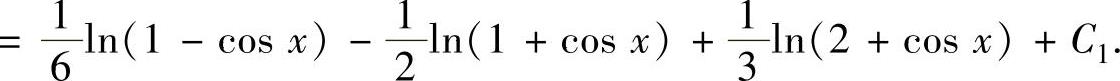有理函数不定积分的计算方法
【主要内容】
1.有理函数不定积分的计算方法
设P(x),Q(x)分别是m,n(m,n都是自然数)次多项式,且它们是不可约的,则称∫PQ((xx))dx为有理函数的不定积分.
当m≥n时,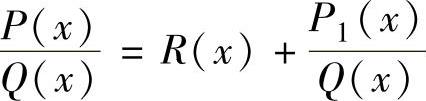 ,其中,R(x)是m-n次多项式,P1(x)是r(r<n)次
,其中,R(x)是m-n次多项式,P1(x)是r(r<n)次
多项式.因此有理函数的不定积分主要考虑计算m<n时的不定积分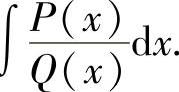 它的计算方
它的计算方
法如下:
先将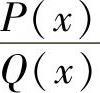 分成部分分式.
分成部分分式.
当Q(x)有因子(x-a)k(k为正整数,且k≤n)时,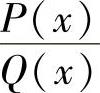 的部分分式中,有形如
的部分分式中,有形如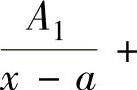
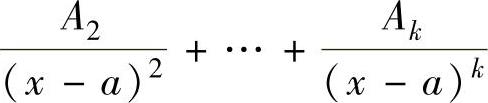 的和项;
的和项;
当Q(x)有因子(x2+px+q)k(k为正整数,且2k≤n以及p2-4q<0)时,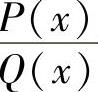 的部分
的部分
分式中,有形如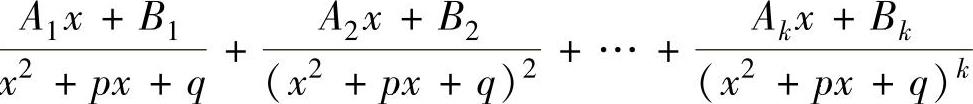 的和项.
的和项.
然后,对P(x)
Q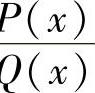 的部分分式的各项积分相加,由此算出不定积分
的部分分式的各项积分相加,由此算出不定积分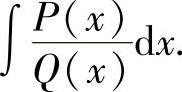
但是,有理函数不定积分的计算,不能拘泥于分部分分式的方法,它应与换元积分法或分部积分法相结合,才能化简整个不定积分计算过程.
2.三角函数有理式、简单无理函数不定积分的计算方法
(1)设R(u,v)是变量u,v的有理式(即由u,v和常数经过有限次四则运算构成的表达式),则称R(sinx,cosx)为三角函数有理式,称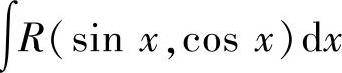 为三角函数有理式的不定
为三角函数有理式的不定
积分,它可由变量代换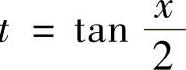 转换成关于t的有理函数的不定积分进行计算.但是使用以
转换成关于t的有理函数的不定积分进行计算.但是使用以
下结论往往会使计算更加快捷:
(ⅰ)如果R(-u,v)=-R(u,v)(即R关于u是奇函数),则令t=cosx;
(ⅱ)如果R(u,-v)=-R(u,v)(即R关于v是奇函数),则令t=sinx;
(ⅲ)如果R(-u,-v)=R(u,v),则令t=tanx.
(2)设R1(u,v)和R2(u,v)都是变量u,v的有理式,则简单无理函数是指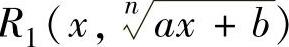 和
和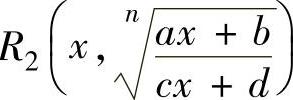 ,其中,n是大于1的整数,a,b,c,d都为常数,且a≠0,c≠0,ad-bc≠0.
,其中,n是大于1的整数,a,b,c,d都为常数,且a≠0,c≠0,ad-bc≠0.
简单无理函数∫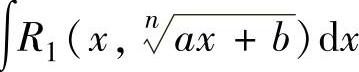 和
和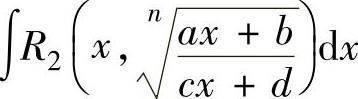 可分别由代换
可分别由代换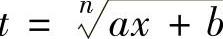 和
和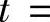
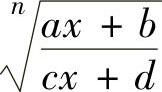 转换成关于t的有理函数的不定积分进行计算.
转换成关于t的有理函数的不定积分进行计算.
【典型例题】
例2.3.1 求不定积分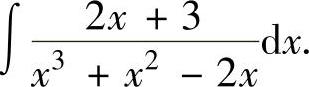
精解 所给的不定积分是有理函数的不定积分,所以先将被积函数分成部分分式.由于x3+x2-2x=x(x2+x-2)=x(x-1)(x+2),
所以,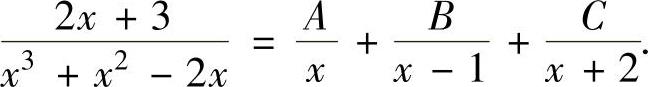 由此可得
由此可得
2x+3=A(x-1)(x+2)+Bx(x+2)+Cx(x-1)
=A(x2+x-2)+B(x2+2x)+C(x2-x)
=(A+B+C)x2+(A+2B-C)x-2A.
比较上式两边关于x的同次幂系数得方程组
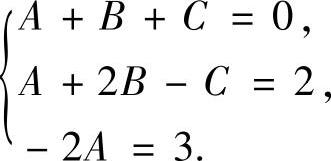
解此方程组得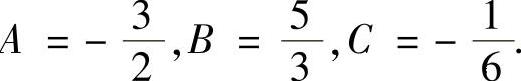 所以
所以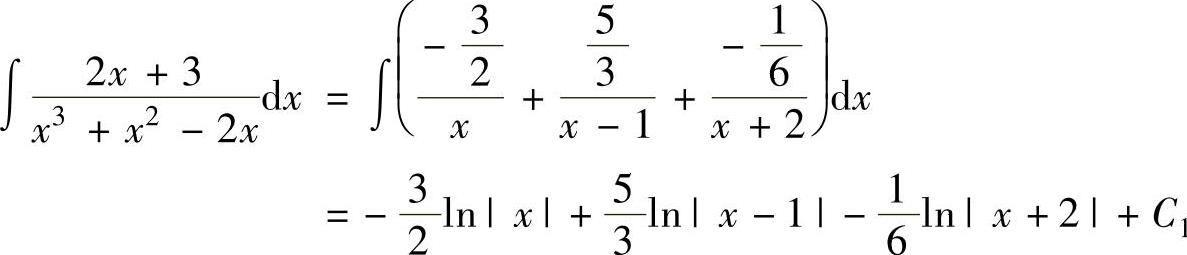 (其中C1为常数).(https://www.daowen.com)
(其中C1为常数).(https://www.daowen.com)
例2.3.2 求不定积分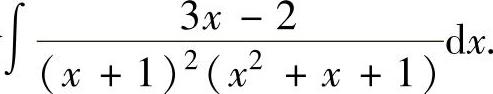
精解 所给的不定积分是有理函数的不定积分,但分母的次数较高,如直接采用分部积分法计算,将是比较复杂的.故先作变量代换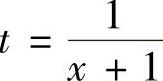 ,将分母中的(x+1)2因子移走,然后再
,将分母中的(x+1)2因子移走,然后再
计算不定积分.
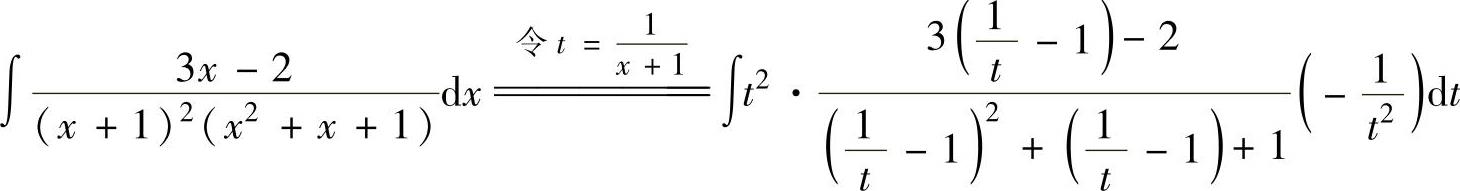
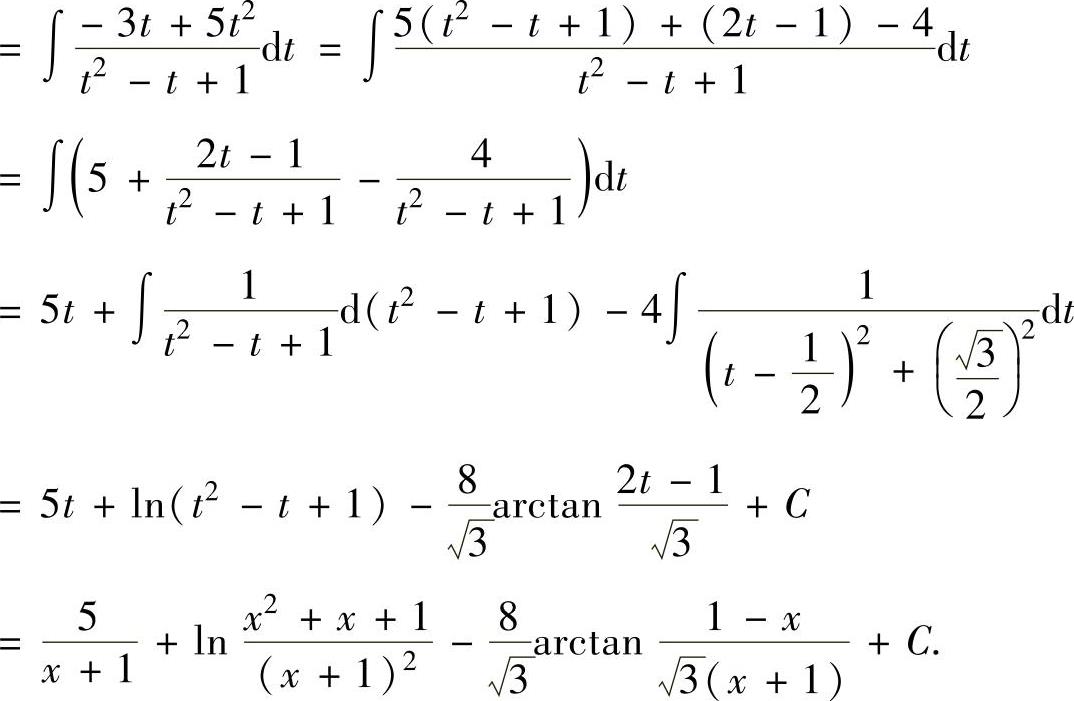
例2.3.3 求不定积分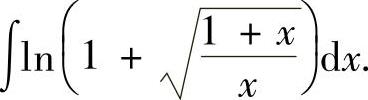
精解 由于被积函数中包含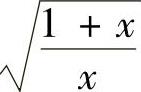 ,所以先作变量代换
,所以先作变量代换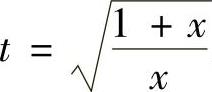 ,并应用分部积分法,
,并应用分部积分法,
把所给不定积分转换成有理函数的不定积分.
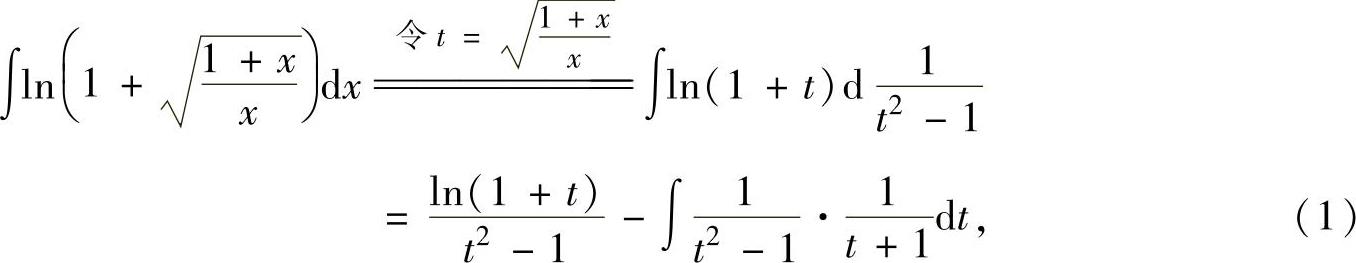
其中,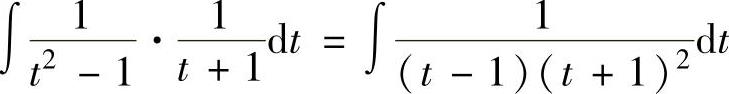 是有理函数的不定积分,因此将被积函数分成部
是有理函数的不定积分,因此将被积函数分成部
分分式:
即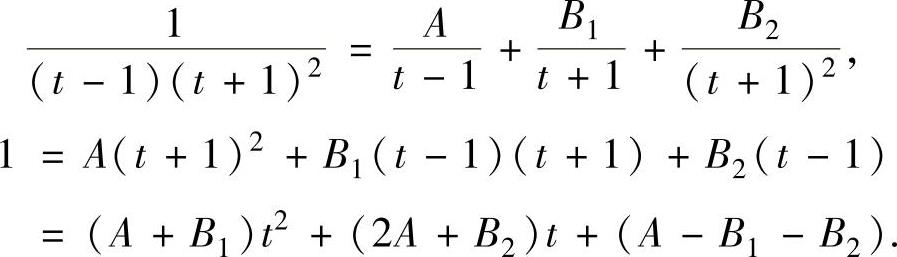
比较上式两边关于t的同次幂系数得
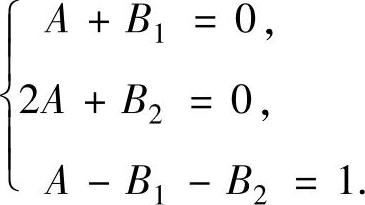
解此方程组得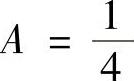 ,B
,B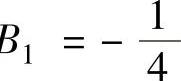 ,B
,B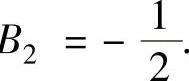 所以,
所以,
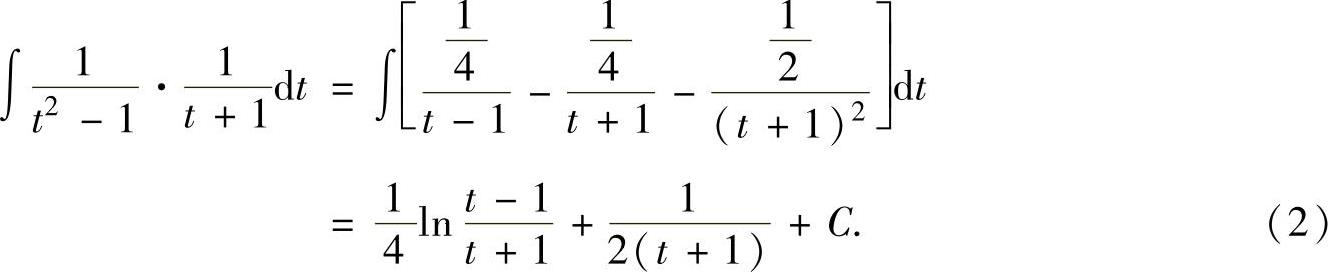
将式(2)代入式(1)得
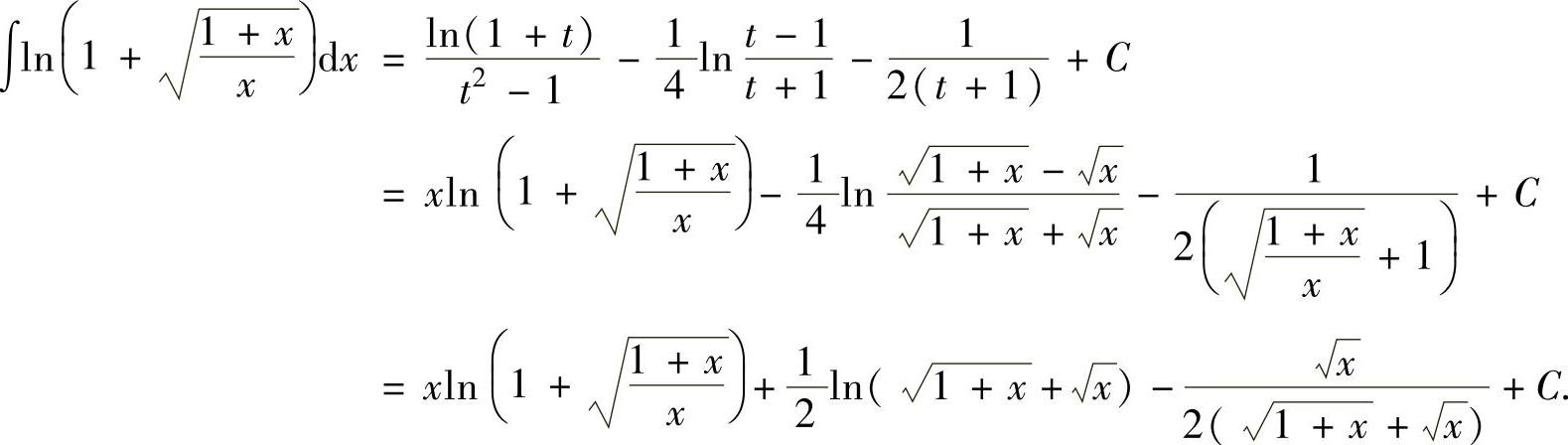
注 本题的被积函数比较复杂,它含有无理函数和对数函数,因此需应用换元积分法和分部积分法,把结果转换成计算有理函数的不定积分,这也是常用的计算不定积分的方法.
例2.3.4 求不定积分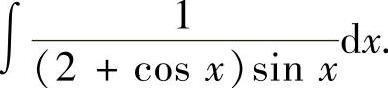
精解 所给的不定积分是三角函数有理式的不定积分(其中,有理式为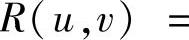
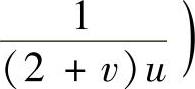 ,因此可以用变量代换
,因此可以用变量代换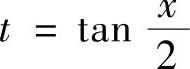 将这个不定积分转换成有理函数的不定积分.但
将这个不定积分转换成有理函数的不定积分.但
是注意到R(-u,v)=-R(u,v),故令t=cosx,将会使计算更简单些.
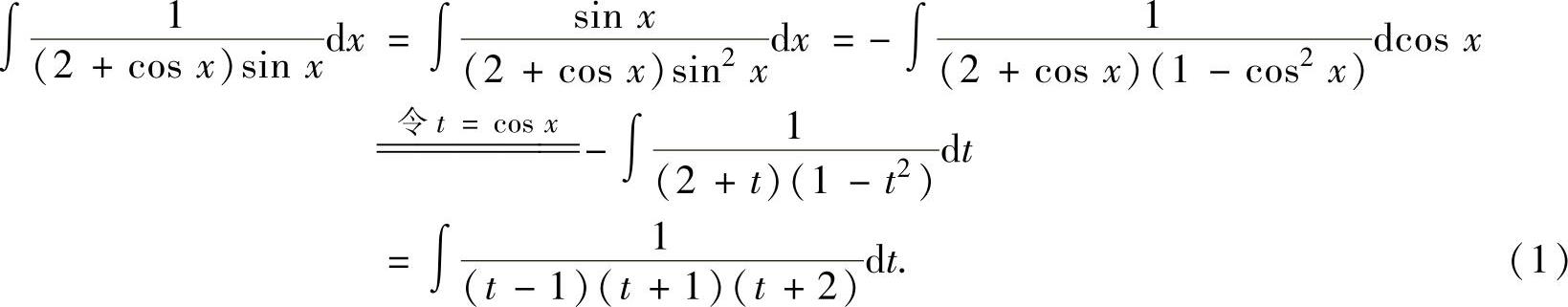
对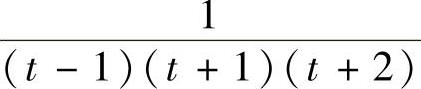 分部分式:
分部分式:
即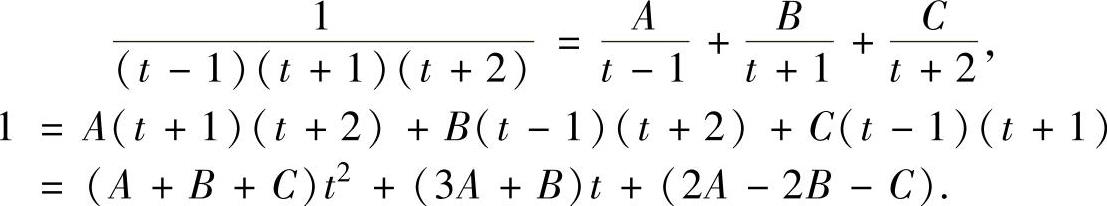
比较上式两边关于t的同次幂系数得
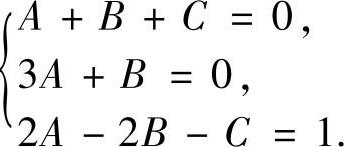
解此方程组得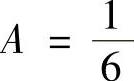 ,
,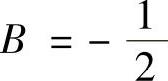 ,
,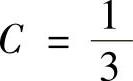 ,所以
,所以
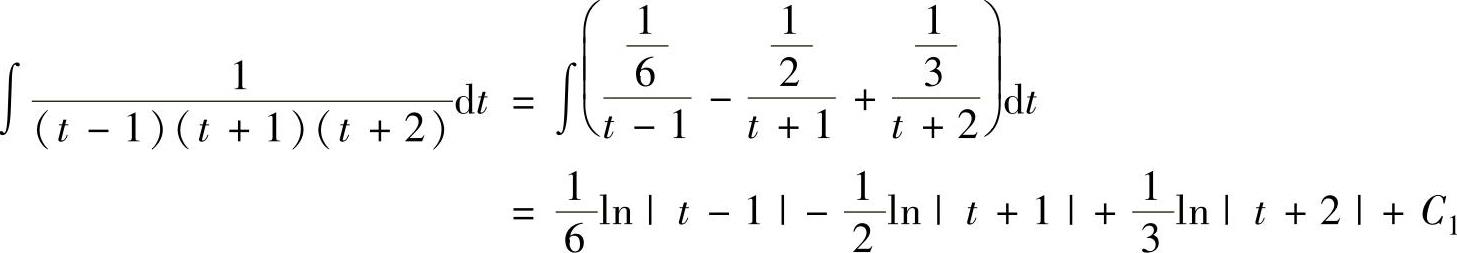
(其中C1为常数)(2)将式(2)代入式(1)得