积分和式极限的计算
2026年01月14日
十
、积分和式极限的计算
【主要内容】
设函数f(x)在[a,b]上有定义,则称极限
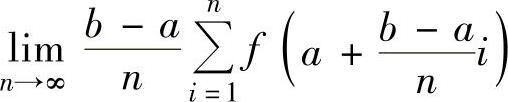
为f(x)在[a,b]上的积分和式极限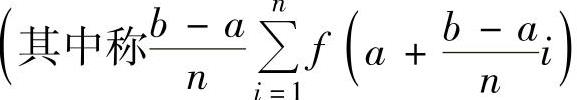 为f(x)在[a,b]上的积分
为f(x)在[a,b]上的积分
和式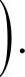
当f(x)在[a,b]上连续时,
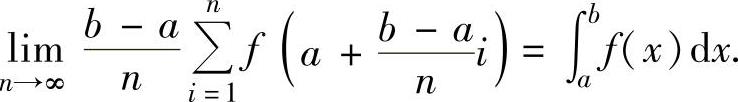
【典型例题】
例2.10.1 (单项选择题)下列等式中不正确的是().
A.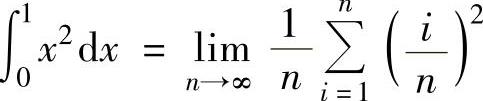 B.
B.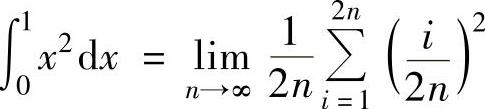
C.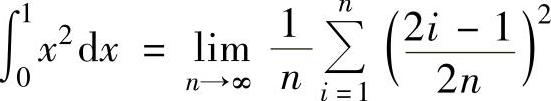 D.
D.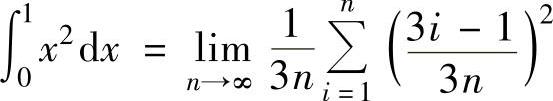
精解 由于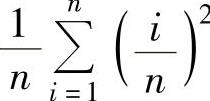 是函数x2在[0,1]上的积分和式
是函数x2在[0,1]上的积分和式 把[0,1]等分成n个小区间
把[0,1]等分成n个小区间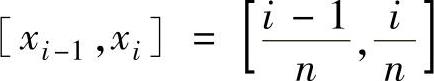 ,i=1,2,…,n,其中,x0=0,xn=1.在每个小区间上任取的点
,i=1,2,…,n,其中,x0=0,xn=1.在每个小区间上任取的点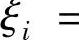
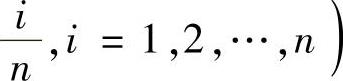 ;由于
;由于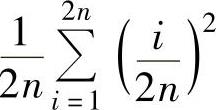 是函数x2在[0,1]上的积分和式
是函数x2在[0,1]上的积分和式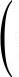 把[0,1]等分成2n个
把[0,1]等分成2n个
小区间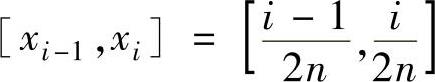 ,i=1,2,…,2n,其中,x0=0,x2n=1,在每个小区间上任取的
,i=1,2,…,2n,其中,x0=0,x2n=1,在每个小区间上任取的
点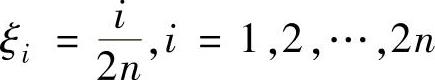
 ;由于
;由于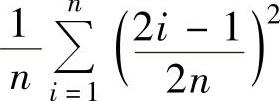 是函数x2在[0,1]上的积分和式
是函数x2在[0,1]上的积分和式 把[0,1]
把[0,1]
等分成n个小区间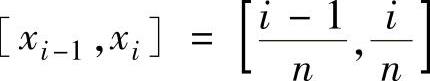 ,i=1,2,…,n,其中,x0=0,xn=1,在每个小区间
,i=1,2,…,n,其中,x0=0,xn=1,在每个小区间
上任取点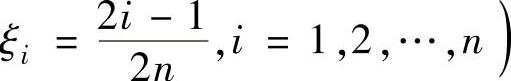 ,所以选项A,B,C都正确.
,所以选项A,B,C都正确.
因此本题选D.
例2.10.2 计算下列和式极限:
(1)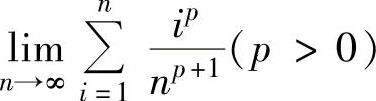 ;
;
(2)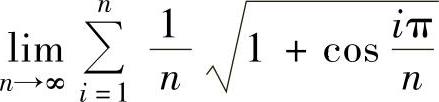 .
.
精解 (1)由于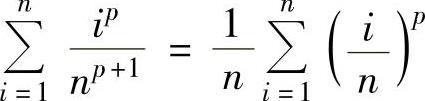 是函数xp在[0,1]上的积分和式,所以
是函数xp在[0,1]上的积分和式,所以
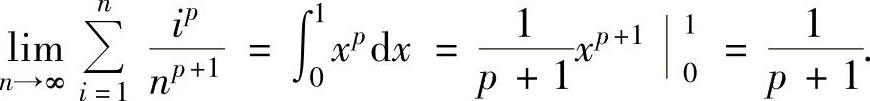
(2)由于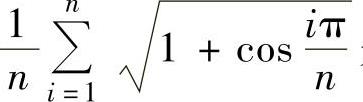 是函数1+cosπx在[0,1]上的积分和式,所以,
是函数1+cosπx在[0,1]上的积分和式,所以,
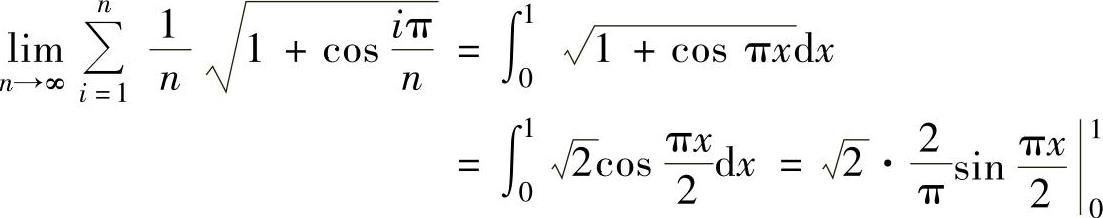
 (https://www.daowen.com)
(https://www.daowen.com)
例2.10.3 计算极限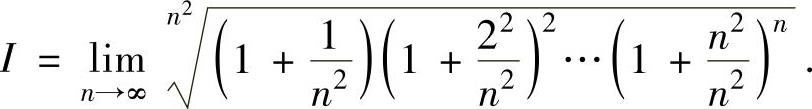
精解 取对数将乘积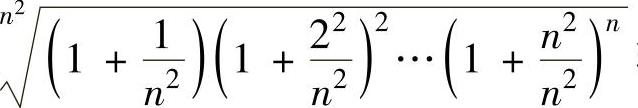 转换成和式:
转换成和式:
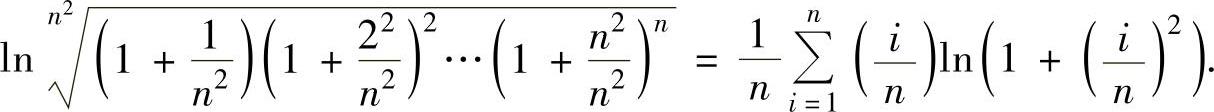
显然,上式右边是函数xln(1+x2)在[0,1]上的积分和式,所以
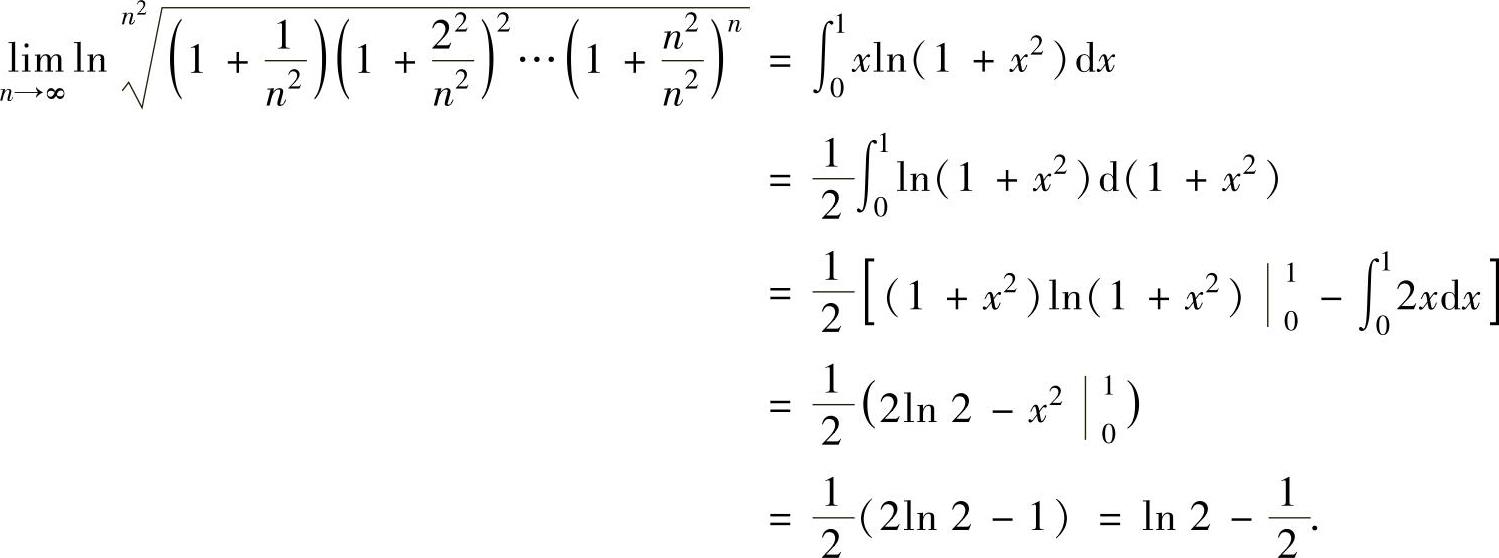
因此,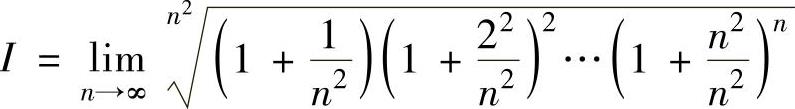
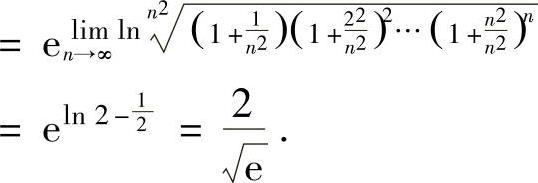
例2.10.4 计算下列和式极限:
(1)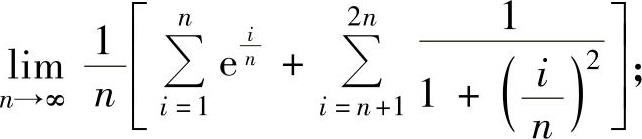
(2)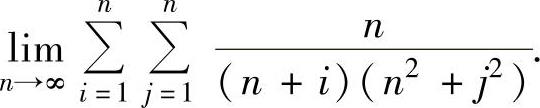
精解 (1)由于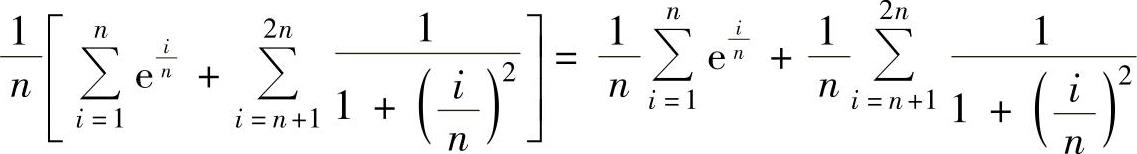 ,
,
其中,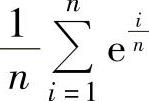 是函数ex在[0,1]上的积分和式;
是函数ex在[0,1]上的积分和式;
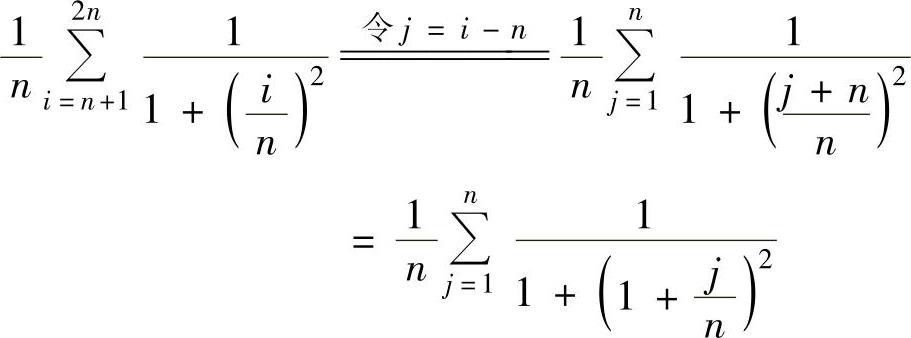
是函数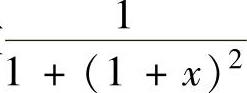 在[0,1]上的积分和式,所以
在[0,1]上的积分和式,所以
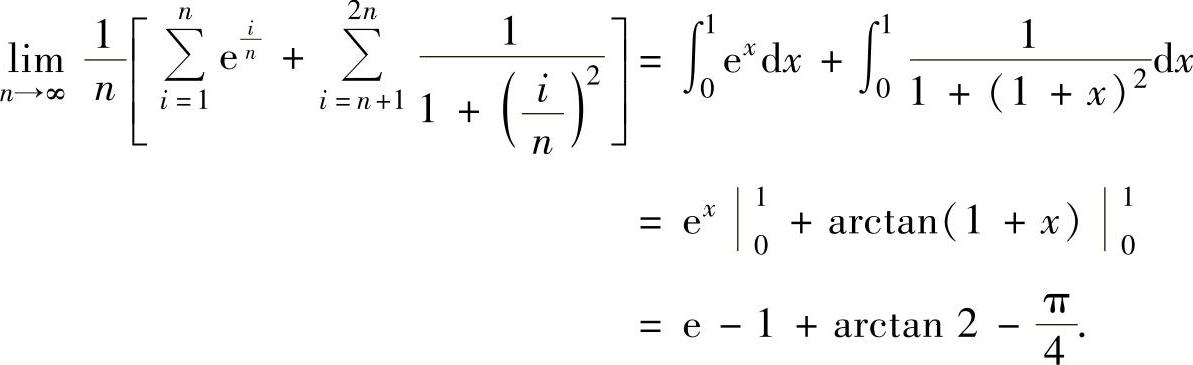
(2)由于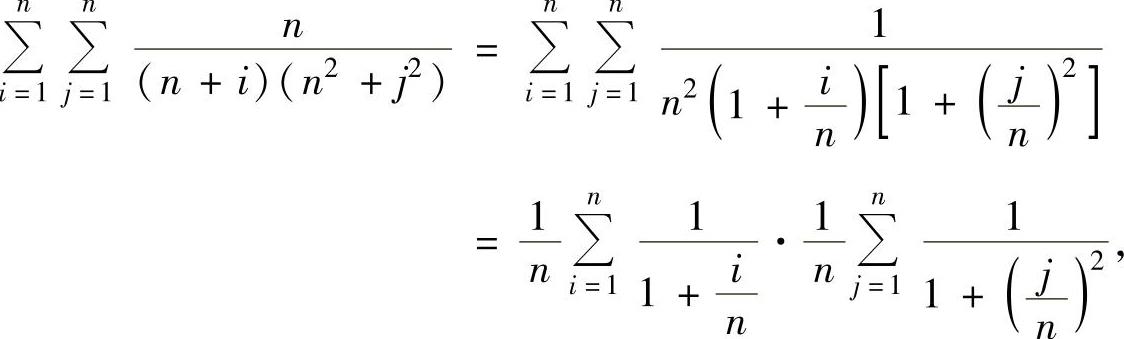
其中,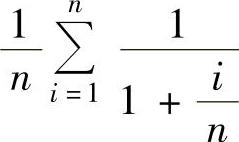 是函数
是函数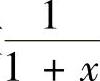 在[0,1]上的积分和式,
在[0,1]上的积分和式,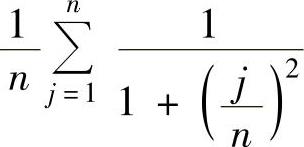 是函数
是函数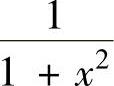 在[0,
在[0,
1]上的积分和式,所以
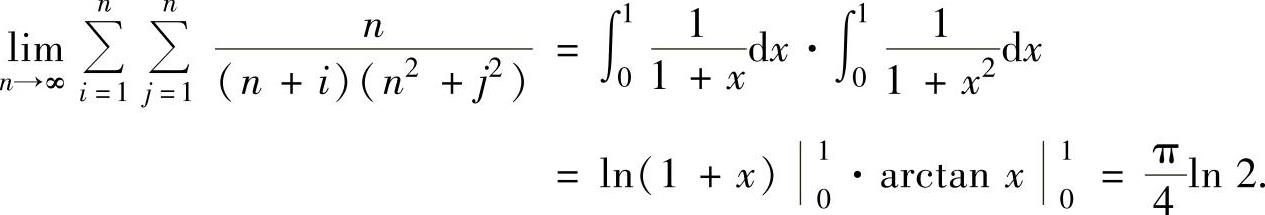
例2.10.5 求和式极限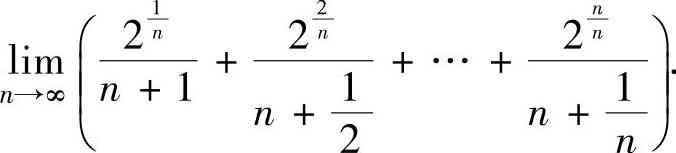
精解 记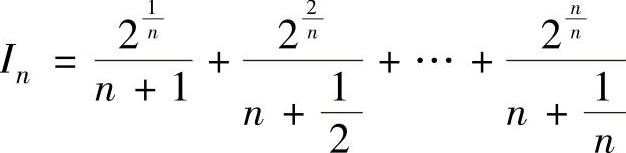 ,它不是某个函数的积分和式,现对它作适当
,它不是某个函数的积分和式,现对它作适当
的缩小与放大:
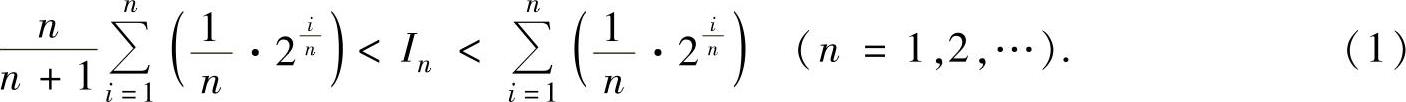
显然,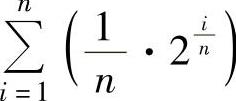 是函数2x在[0,1]上的积分和式,所以
是函数2x在[0,1]上的积分和式,所以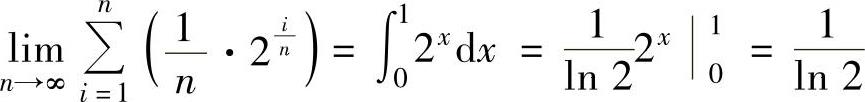 ,
,
并且,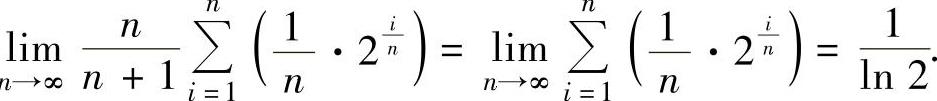
因此,由数列极限存在准则Ⅰ得