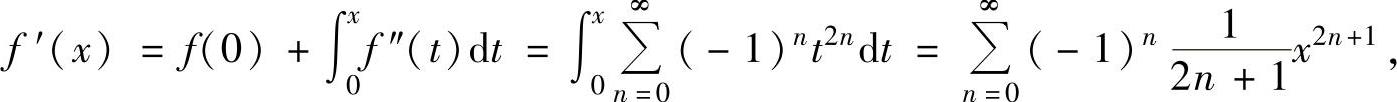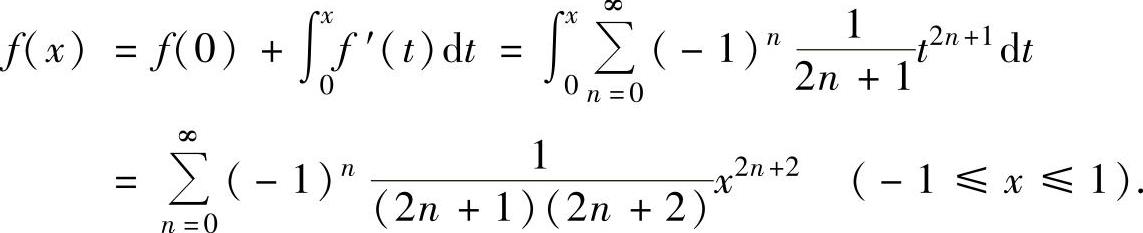练习题四解答
一、单项选择题
(1)B (2)D (3)D (4)A (5)D (6)B
(7)D (8)B (9)B (10)C (11)C
(12)A (13)C (14)B (15)C (16)B
(17)D (18)C (19)A (20)A (21)C
二、解答题
(1)通解为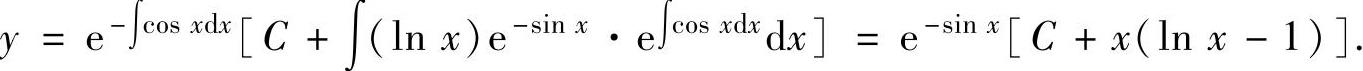
(2)令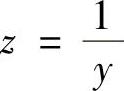 ,则所给微分方程成为
,则所给微分方程成为
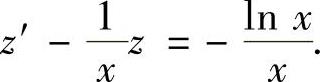
它的通解为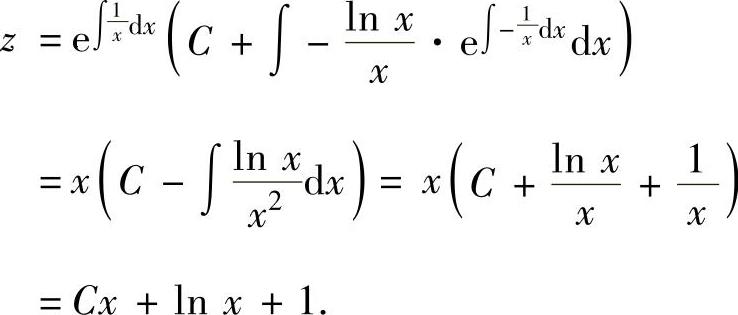
所以原微分方程的通解为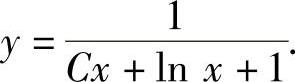
(3)将所给微分方程改写成

令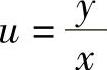 ,则有
,则有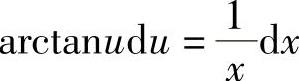 ,即
,即
所以,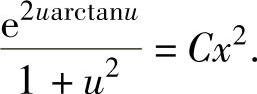 因此原微分方程的通解为
因此原微分方程的通解为
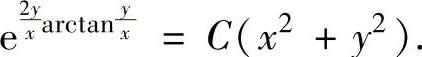
(4)令z=y2,则所给微分方程成为
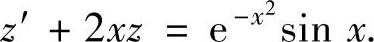
它的通解为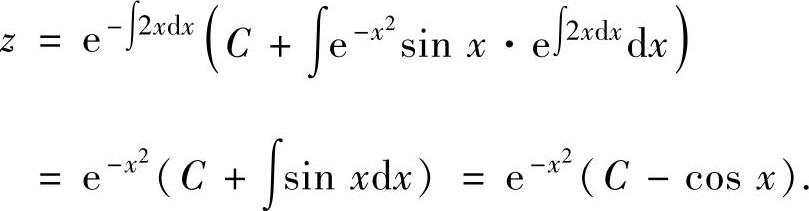
所以原微分方程的通解为
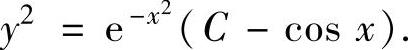
(5)将微分方程改写成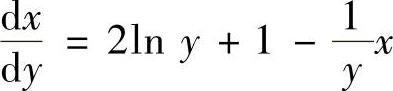 ,即
,即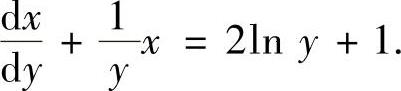
它的通解为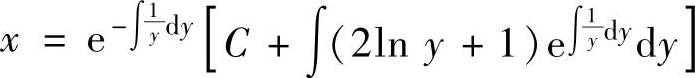
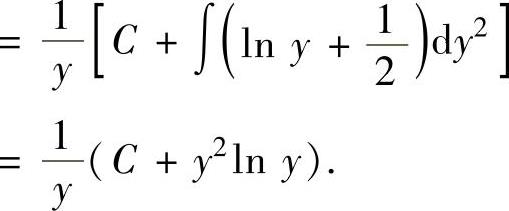
(6)令p=y′,则所给微分方程成为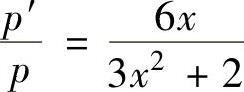 ,
,
所以p=C1(3x2+2),即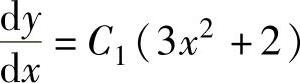 .因此y=C1x3+2C1x+C2.
.因此y=C1x3+2C1x+C2.
要使x→0时y与ex-1是等价无穷小,必须满足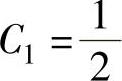 ,C2=0.所以所求的解为
,C2=0.所以所求的解为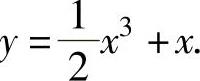
(7)将所给微分方程改写成
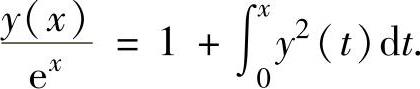
上式两边对x求导得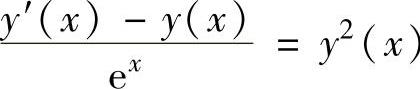 ,即y′-y=exy2.
,即y′-y=exy2.
记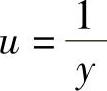 ,则上述微分方程成为u′+u=-ex,它的通解为
,则上述微分方程成为u′+u=-ex,它的通解为
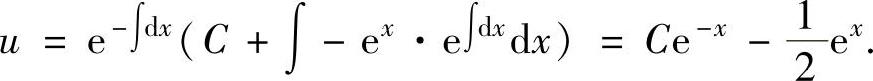
由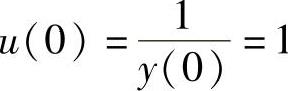 得
得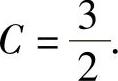 所以
所以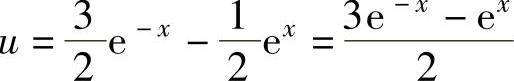 ,从而
,从而
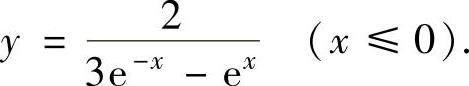
(8)所给等式可化简为
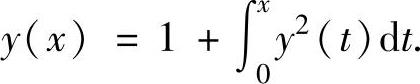
两边对x求导得y′=y2,所以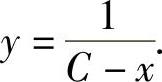 将y(0)=1代入得C=1.所以所求的
将y(0)=1代入得C=1.所以所求的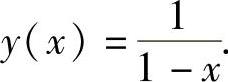
(9)所给微分方程对应的齐次线性微分方程的特征方程是r2+4=0其根为-2i,2i,所以其通解为Y=C1cos2x+C2sin2x.根据微分方程右边的函数知,所给微分方程应有特解
y∗=(a0+a1x+a2x2)+x(b1cos2x+b2sin2x)+(c1cosx+c2sinx).
将它代入所给微分方程得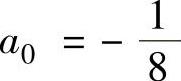 ,
,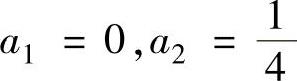 ,
,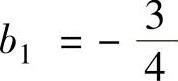 ,
,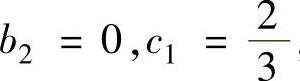 ,c2=0.
,c2=0.
所以,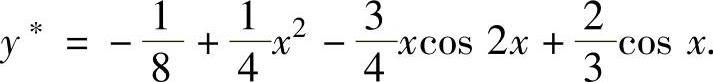 因此通解为
因此通解为
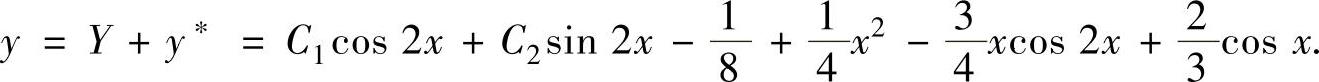
(10)所给微分方程对应的齐次线性微分方程的特征方程是r2+a2=0,其特征根为ia,-ia,所以,它的通解为Y=C1cosax+C2sinax.
当a≠1时,原微分方程有特解y∗=Acosx+Bsinx.将它代入原微分方程得(https://www.daowen.com)
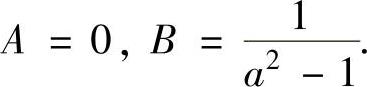
所以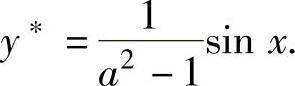 从而原微分方程的通解为
从而原微分方程的通解为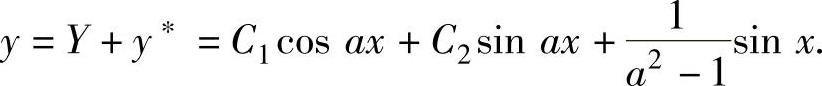
当a=1时,原微分方程有特解y∗=x(A1cosx+B1sinx),将它代入原微分方程得
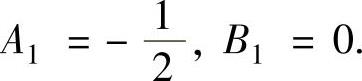
所以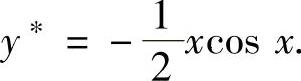 从而原微分方程的通解为
从而原微分方程的通解为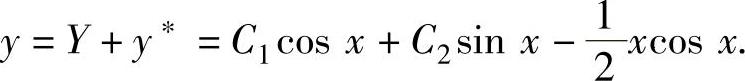
(11)由于原式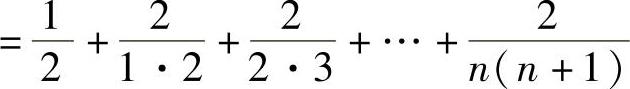
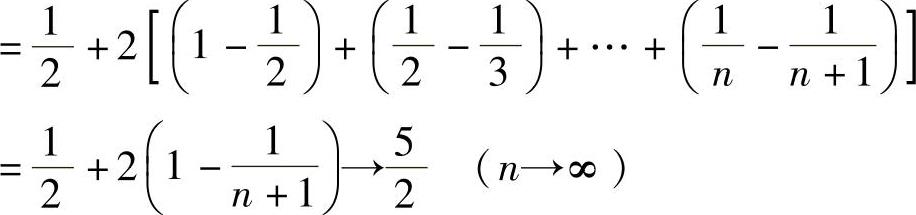
所以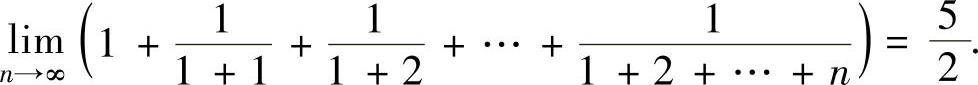
(12)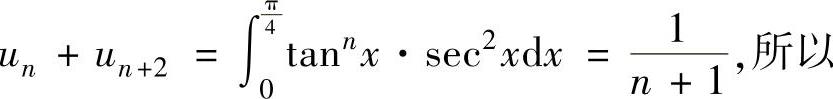
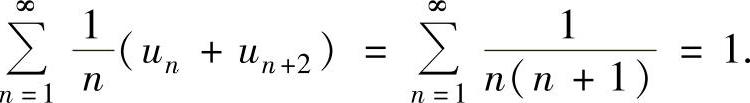
(13)所给级数都为正项级数.
记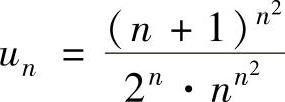 ,则lim
,则lim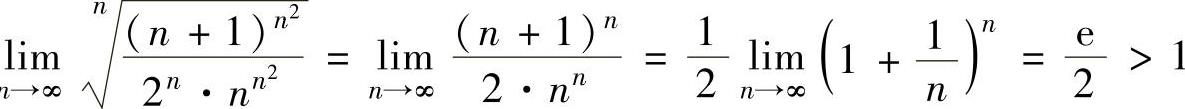 所
所
以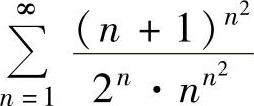 发散.记
发散.记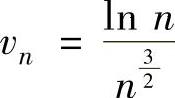 ,则
,则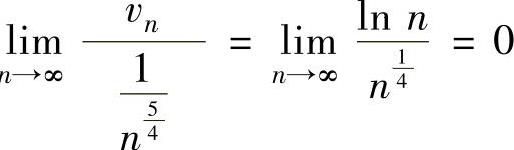 ,且
,且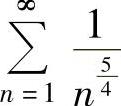 收敛,所以
收敛,所以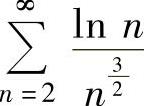 收敛.
收敛.
(14)(ⅰ)由于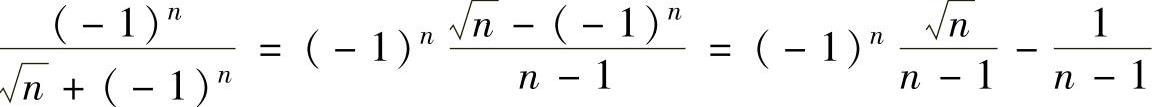 ,
,
其中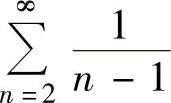 发散.对于交错级数
发散.对于交错级数
n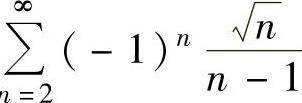 ,记f
,记f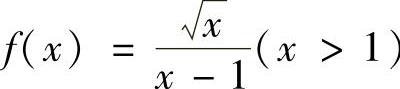 ,则由
,则由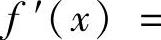
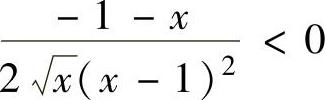 知数列
知数列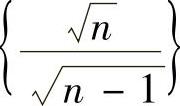 单调减少,且
单调减少,且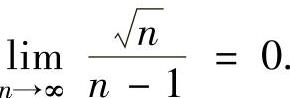 所以由莱布尼茨定理知
所以由莱布尼茨定理知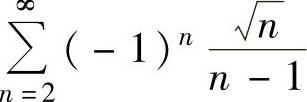 收敛.从而
收敛.从而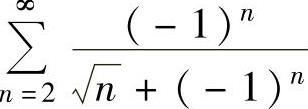 发散.
发散.
(ⅱ)记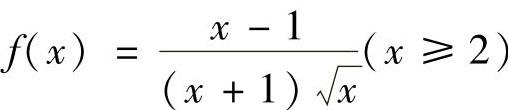 ,则由
,则由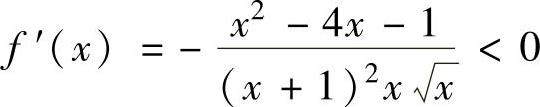 (当x充分大时)
(当x充分大时)
可认为数列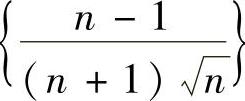 单调减少,且
单调减少,且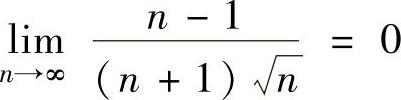 ,所以由莱布尼茨定理知
,所以由莱布尼茨定理知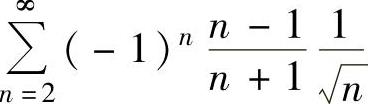 收敛.此外
收敛.此外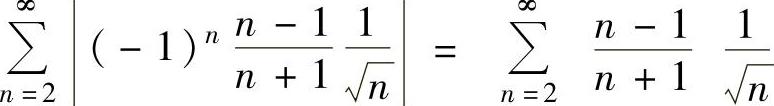 发散.所以
发散.所以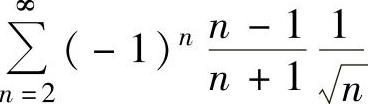 条件收敛.
条件收敛.
(15)记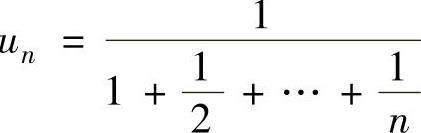 ,则
,则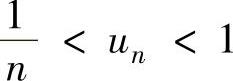 ,即
,即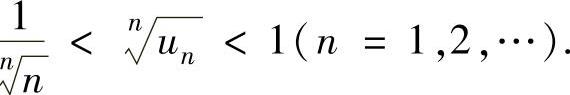 从而
从而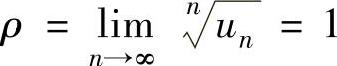 ,即收敛半径R=1.
,即收敛半径R=1.
当x=1时,所给幂级数成为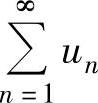 ,它是发散的.
,它是发散的.
当x=-1时,所给幂级数成为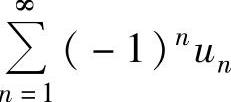 (交错级数),由于{un}单调减少且收敛于零,
(交错级数),由于{un}单调减少且收敛于零,
所以该级数收敛.
从而所给幂级数的收敛域为[-1,1).
(16)记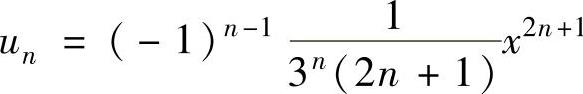 ,则
,则
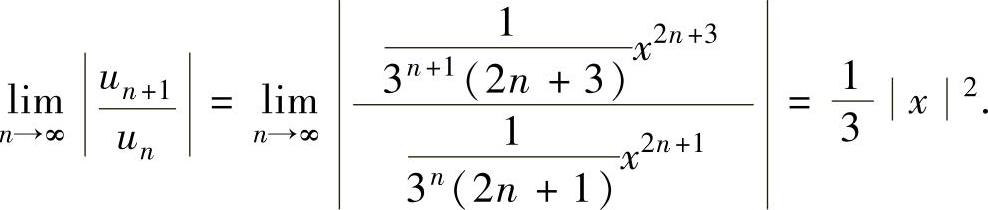
所以收敛区间为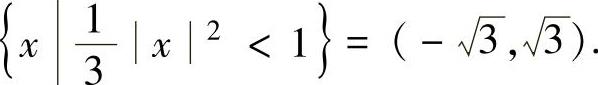
当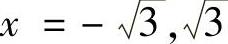 时,所给的幂级数分别成为级数
时,所给的幂级数分别成为级数
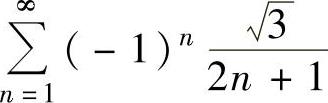
和
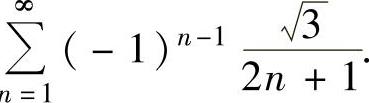
由莱布尼茨定理知它们都是收敛的,因此所给幂级数的收敛域为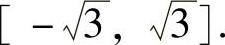
记和函数为s(x),即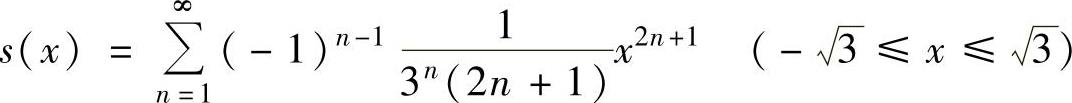
在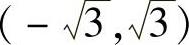 内,
内,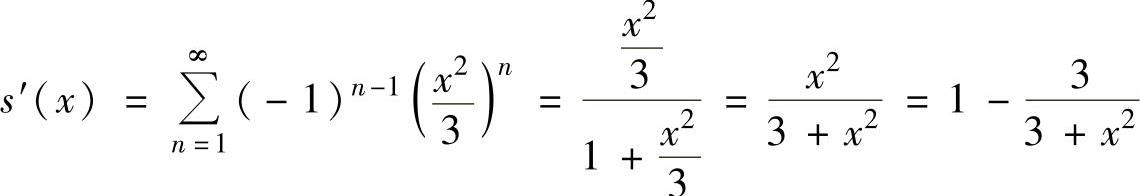 ,所以
,所以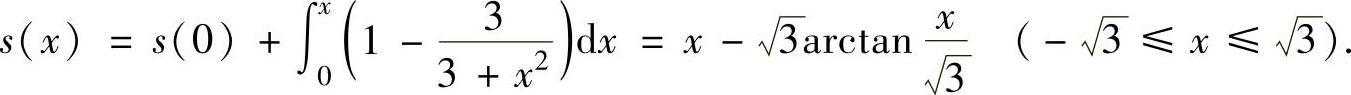
(17)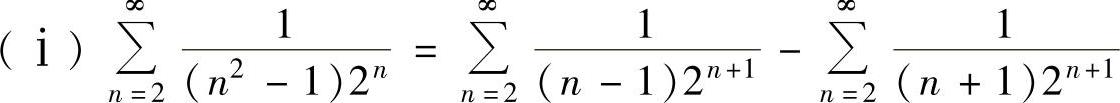
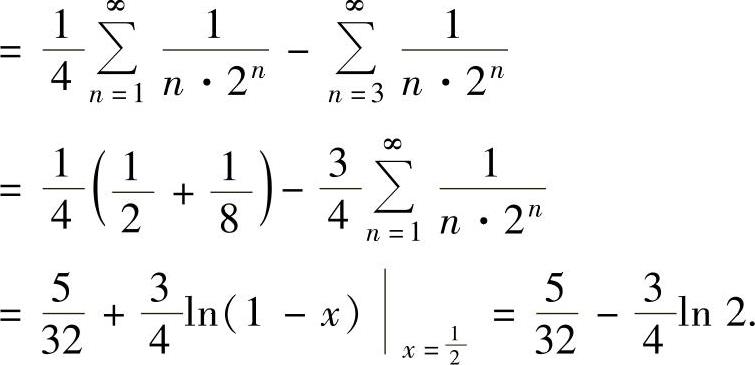
(ⅱ)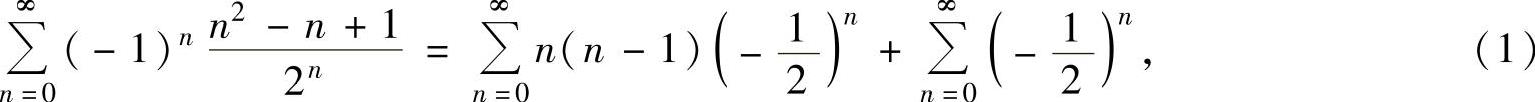
其中,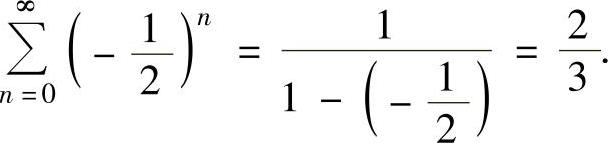 为了计算
为了计算
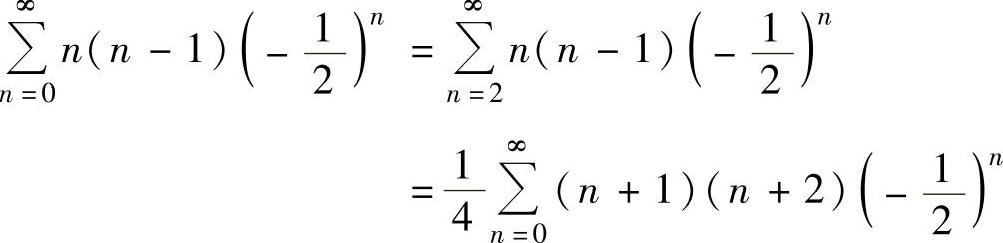
考虑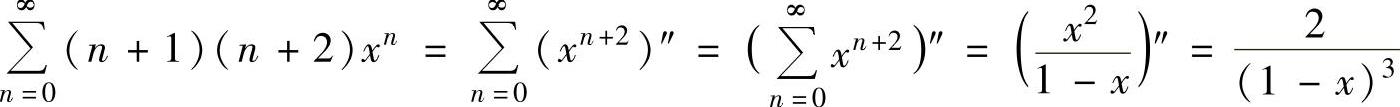 ,
,
所以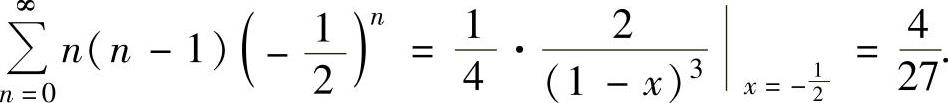
将它们代入式(1)得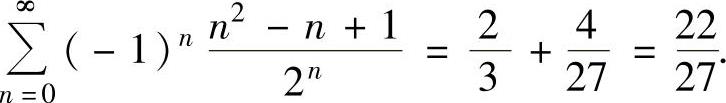
(18)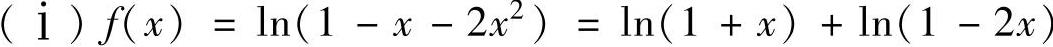
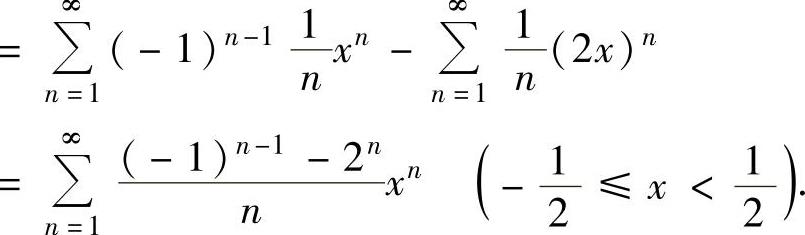
(ⅱ)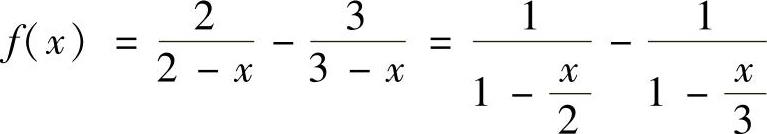
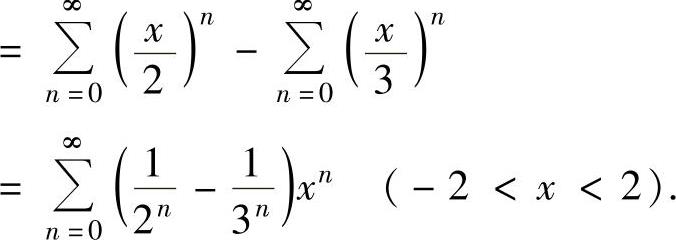
(19)由于 f(0)=0,f′(x)=arctanx,f′(0)=0,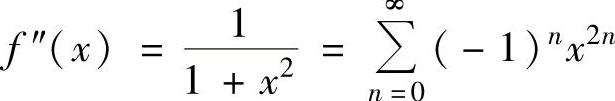 ,
,
所以