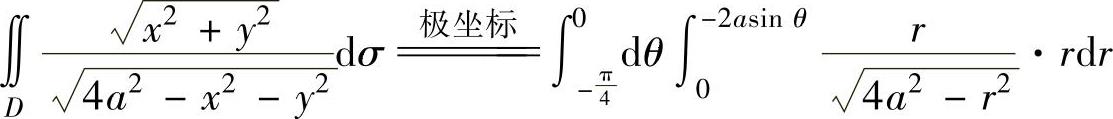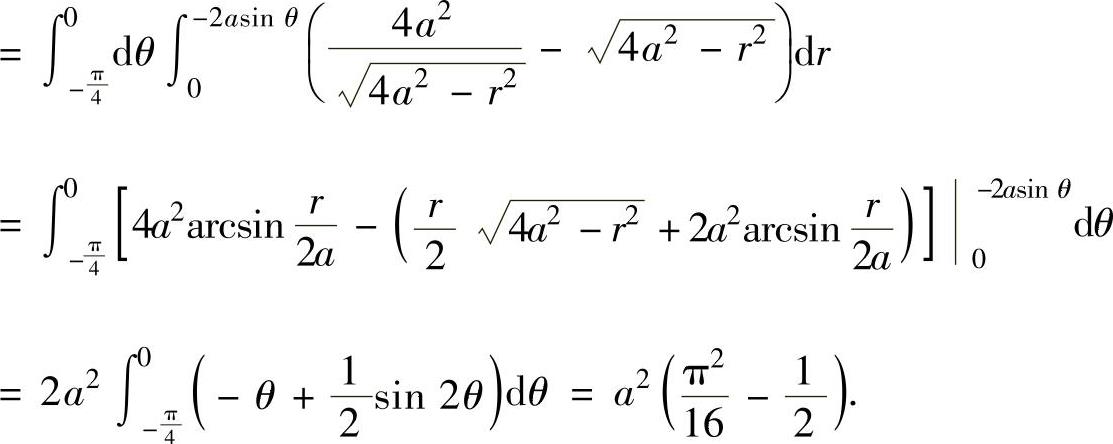练习题三解答

练习题三解答

1.单项选择题

（1）A （2）C （3）D （4）B （5）C

（6）C （7）D （8）C （9）D （10）D

（11）A （12）A （13）C （14）B

2.解答题

（1）φ′（x）=f₁′·2x+f₂′（f₁′·2x+f₂′），φ′（1）=2×2+3（2×2+3）=25.

（2）对所给方程两边求全微分

dz-dx-dy+ye^z-xdx+xe^z-xdy+xye^z-x（dz-dx）=0，即（1+xye^z-x）dz=（1-ye^z-x+xye^z-x）dx+（1-xe^z-x）dy，

所以，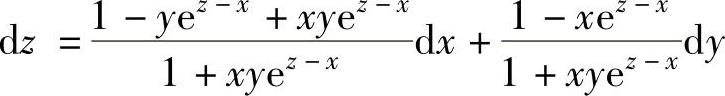

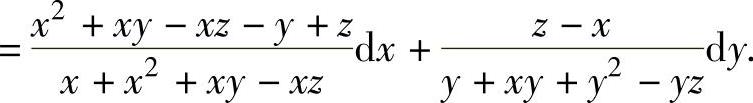
（3）由dz=d[e（x+y）lnx+（x+1）ln（1+y）]

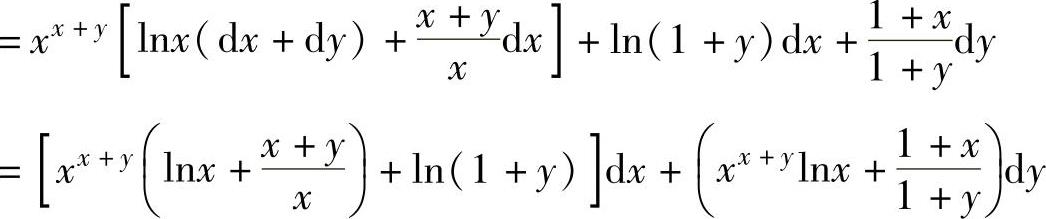
所以，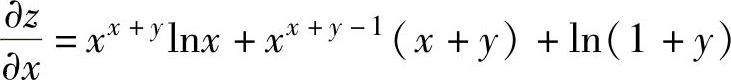

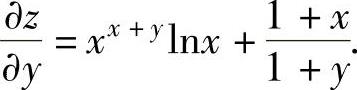
（4）当x²+y²≠0时，，并且，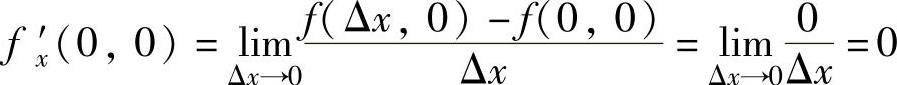

所以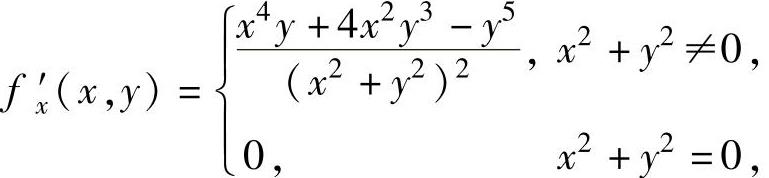

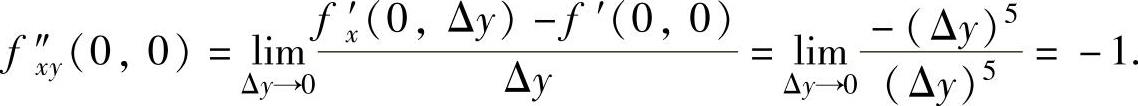
（5）由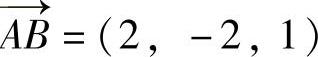知其方向余弦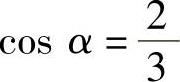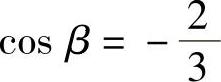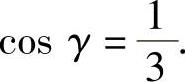，，因此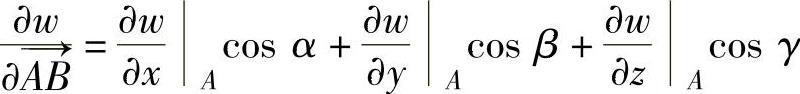

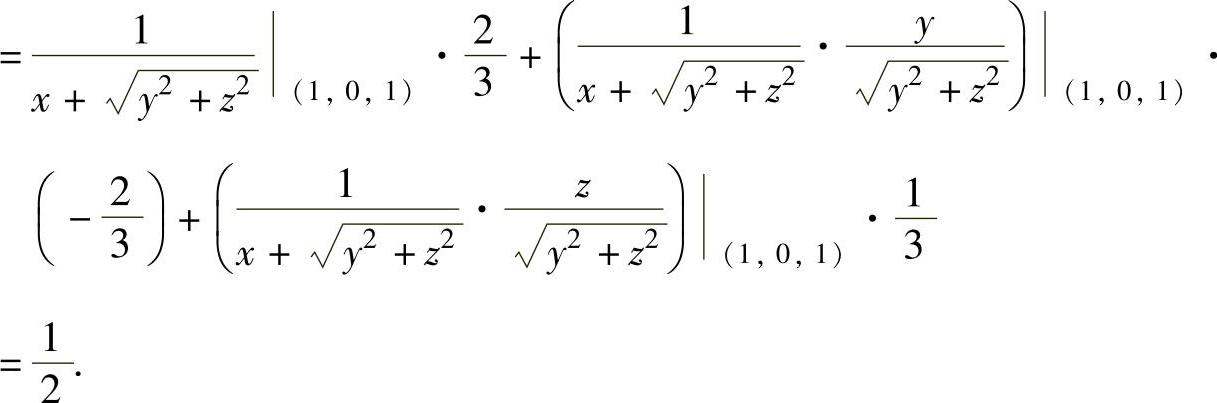
（6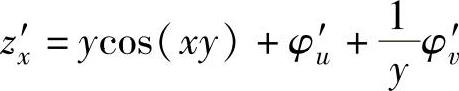）其中，u=x，v=x，所以y

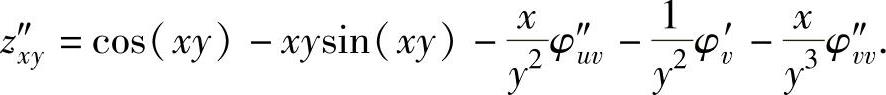
（7）记u=xg（y），v=y，则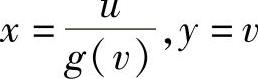，所以所给关系式成为，

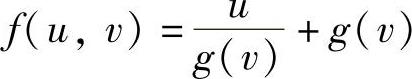从而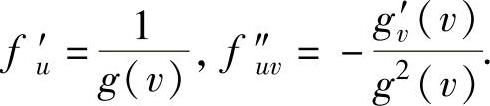

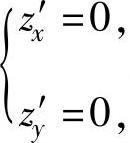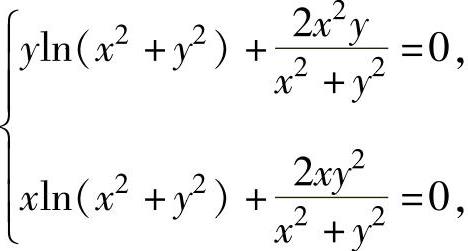（8）z的定义域为除去点（0，0）的xOy平面，由即得x=0，

y=0，x=y，x=-y.由此得z的可能极值点为

（0，1），（0，-1），（1，0），（-1，0），，，，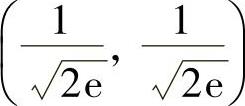

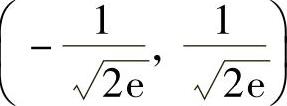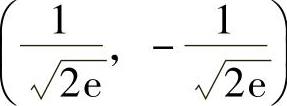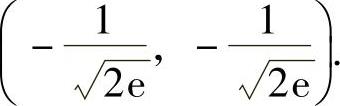
显然z（0，1）=z（0，-1）=z（1，0）=z（-1，0）=0都不是极值.

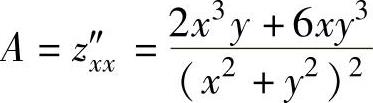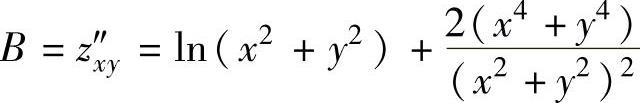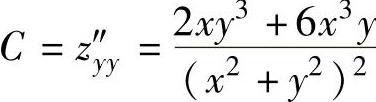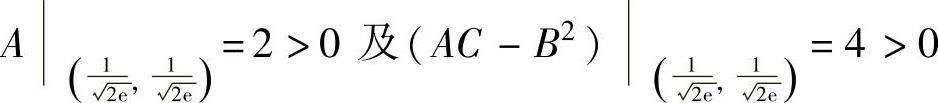记，，，则由知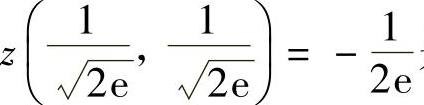是极小值，同样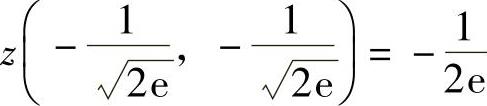也是极小值.

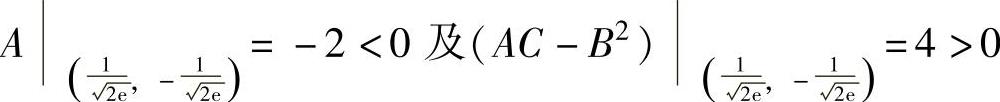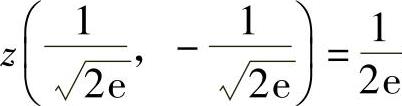由知是极大

值，同样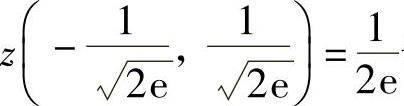也是极大值.

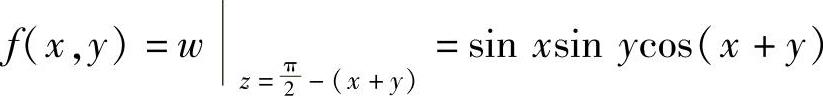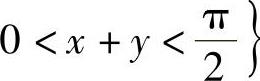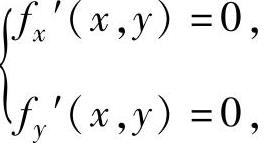（9）记，（x，y）∈D={（x，y）x>0，y>0，，由于即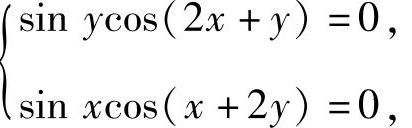

所以f（x，y）在D内只有唯一的可能极值点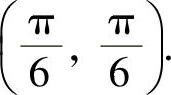记(https://www.daowen.com)

A=f″_xx（x，y）=-2sinysin（2x+y），B=f″_xy（x，y）=cos（2x+2y），

C=f_y″_y（x，y）=-2sinxsin（x+2y），

则由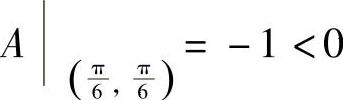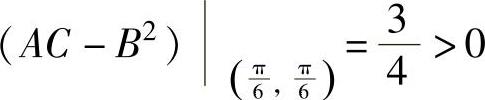，知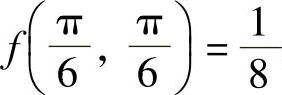，是f（x，y）在D内的最

大值.由于f（x，y）>0（（x，y）∈D），但limf（x，y）=0，所以f（x，y）在D内无最小值.

（x，y）→（0，0）

由上可知，w（x>0，y>0，z>0）在约束条件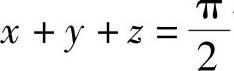下的最大值为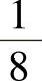，无最小值.

（10）记φ（x，y，z）=x²+y²+z²-1，ψ（x，y，z）=x+y+z及

F（x，y，z）=xyz+λφ（x，y，z）+μψ（x，y，z）.显然F处处可微，且

F_x′ =yz+2λx+μ，

F_y′ =xz+2λy+μ，

F_z′ =xy+2λz+μ.

于是由拉格朗日乘数法得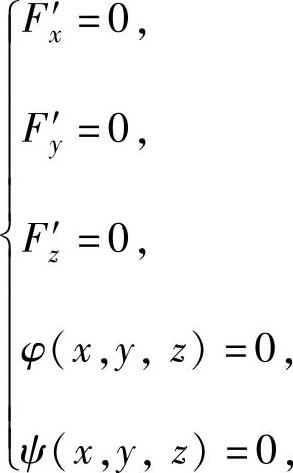即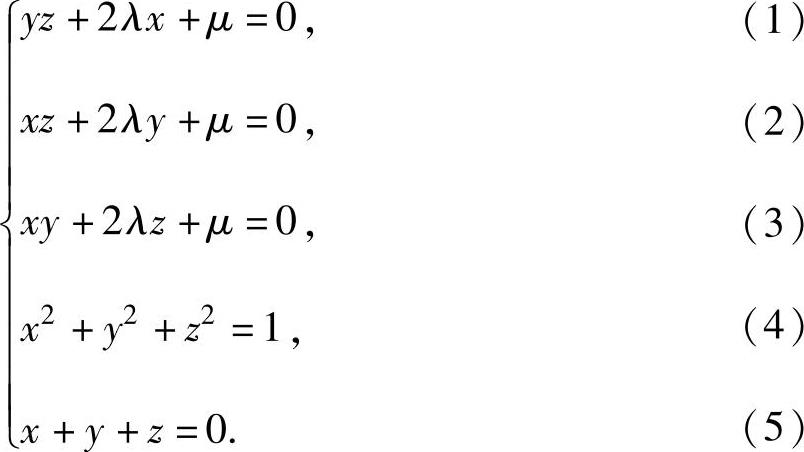

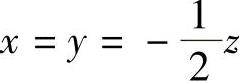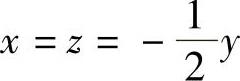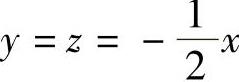解此方程组的（1）、（2）、（3）、（5）得，或，，所以由式

（4）得xyz在约束条件φ=0和ψ=0下的可能极值点为，，，，，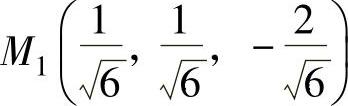

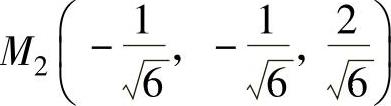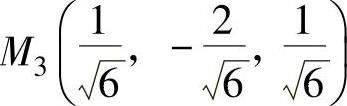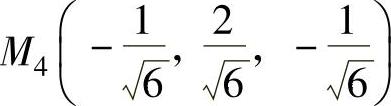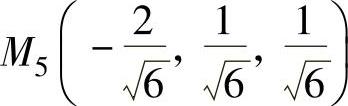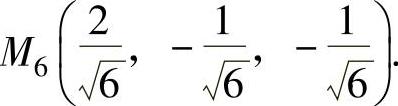
由于w是连续函数，它可在曲线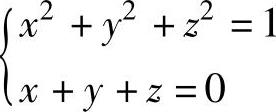，上取得最大值与最小值，而且只能在点

M₁，M₂，M₃，M₄，M₅，M₆上取到.由于

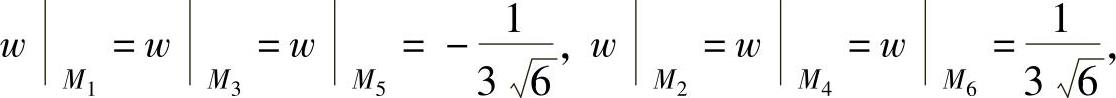
所以，w在约束条件φ=0和ψ=0下的最大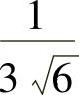值为，最小值为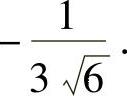

（11）由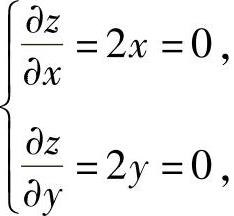得x=y=0，即z在D内有唯一可能极值点（0，0）.

为了考虑z=x²+y²在D的边界（x-2）2+（y-2）2=9上的最值，记F（x，y）=x²+y²+，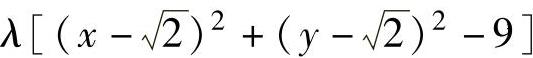

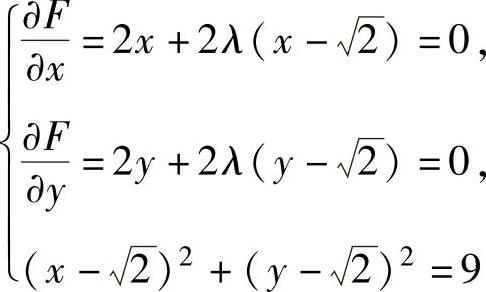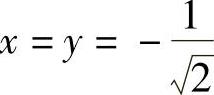由得与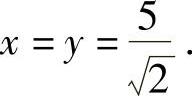

由于z（0，0）=0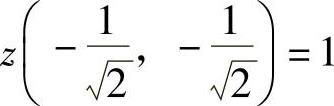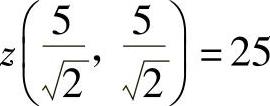，，，所以z在D上的最大值为25，最

小值为0.

（12）

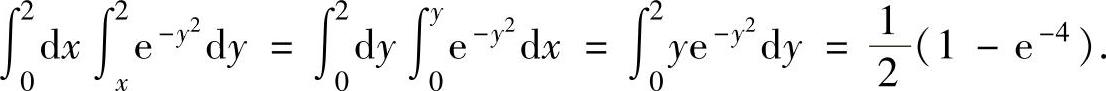
（13）由于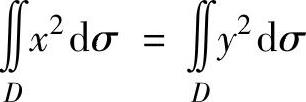，所以

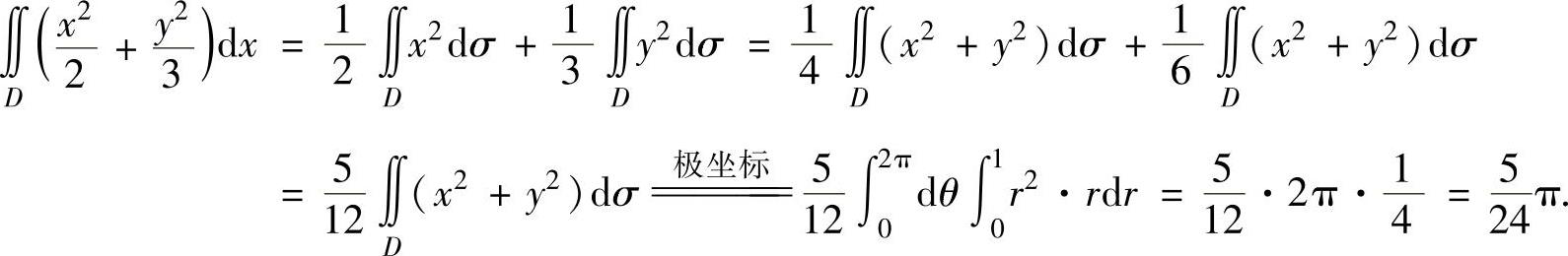
（14），

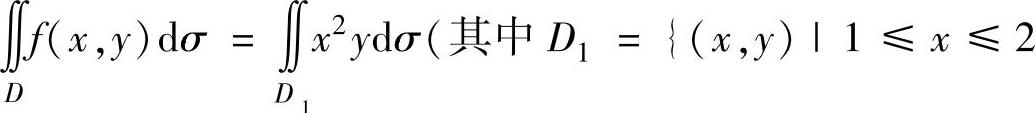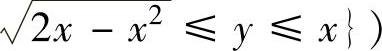
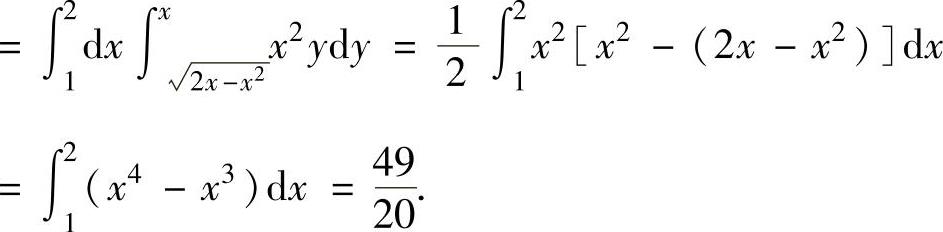
（15）记D₁={（x，y）|x²+y²≤1}，D₂=D-D₁，则

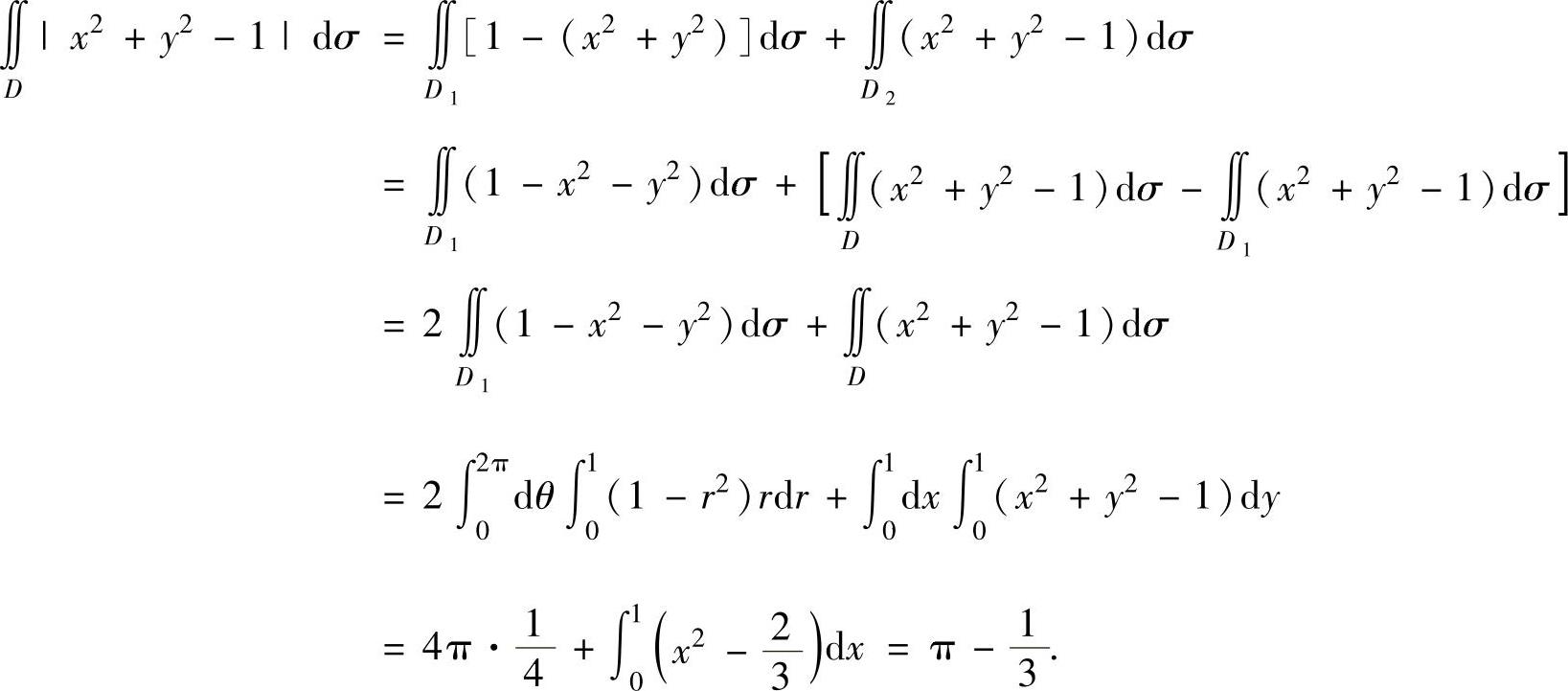
（16）