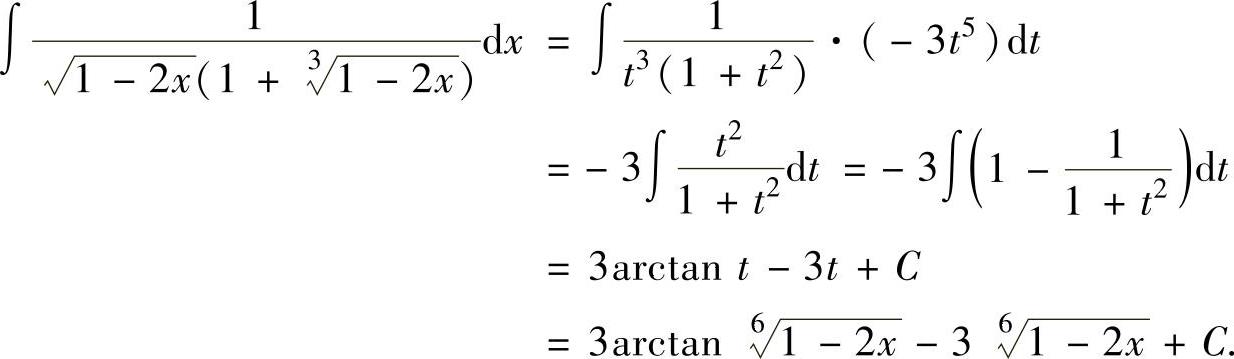不定积分的换元积分法
【主要内容】
1.不定积分的概念
函数f(x)在区间I上的原函数全体F(x)+C(其中,F(x)是f(x)的一个原函数,即F′(x)=f(x),C是任意常数),称为f(x)的不定积分,记为∫f(x)dx.
不定积分的计算主要依靠不定积分的基本公式、基本性质及基本运算方法.
基本公式
(1)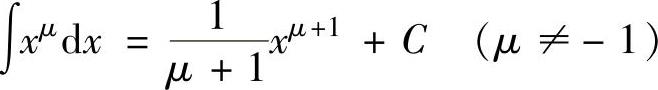 ,
,
(2)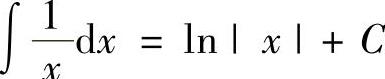 ,
,
(3)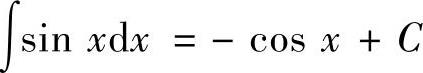 ,
,
(4)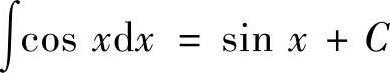 ,
,
(5)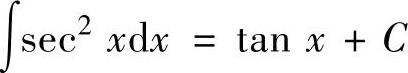 ,
,
(6)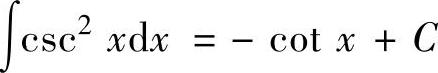 ,
,
(7)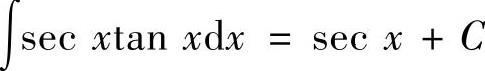 ,
,
(8)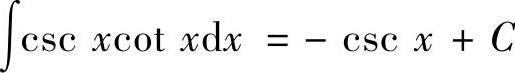 ,
,
(9)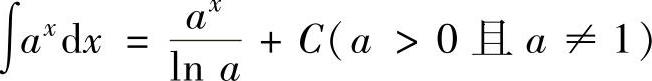 ,特别地,
,特别地,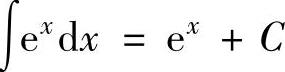 ,
,
(10) ,
,
(11)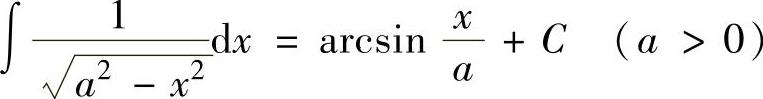 ,
,
(12)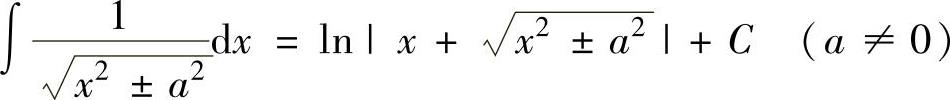 ,
,
此外,还有
(13) ,
,
(14)
(15)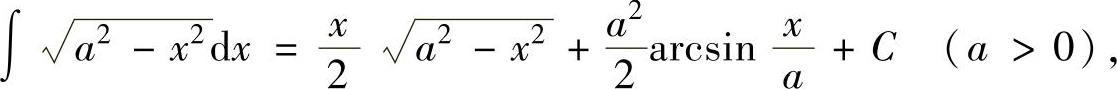
(16)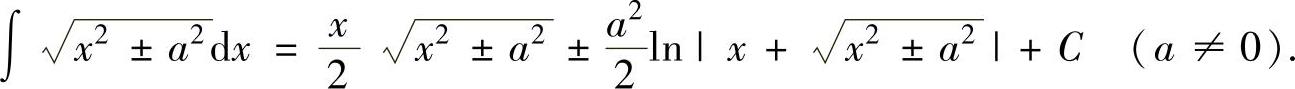
基本性质
设函数f(x),g(x)的原函数存在,k为常数,则
(1)
(2)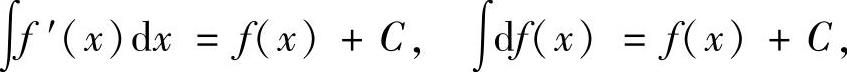
(3)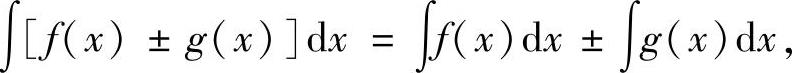
(4)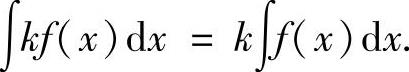
基本运算方法
(1)换元积分法;
(2)分部积分法(放到下一节讲).
2.不定积分的换元积分法
换元积分法就是通过适当的变量代换(简称换元),将要求的不定积分转换成基本公式中的不定积分,从而算出要求的不定积分,即
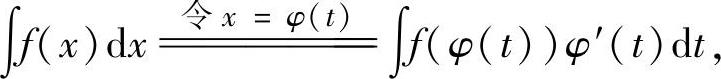
或者
如果以上两式中右边的不定积分都是基本公式中的不定积分,则由此算出左边要求的不定积分.(https://www.daowen.com)
注 用换元积分法计算不定积分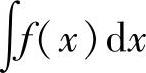 时,采用什么样的变量代换,应视具体情况而
时,采用什么样的变量代换,应视具体情况而
定,但以下两点值得注意:
(ⅰ)如果f(x)是一个分式,而分母比较复杂,为去掉分母中的某些因子,或将分母中的某些因子移到分子中去,使分母变得简单些,可使用变量代换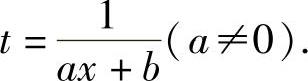
(ⅱ)如果f(x)中含有根式,则作变量代换将根式去掉,例如,
当f(x)中含有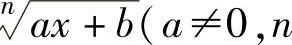 是大于1的正整数)时,可令
是大于1的正整数)时,可令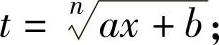
当f(x)中含有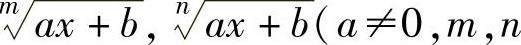 都是大于1的正整数)时,可令
都是大于1的正整数)时,可令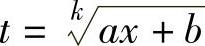 ,其
,其
中,k是m,n的最小公倍数;
当f(x)中含有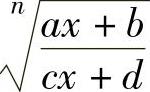 (其中a,c都不为零,且ad≠bc,n是大于1的正整数)时,可令
(其中a,c都不为零,且ad≠bc,n是大于1的正整数)时,可令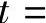
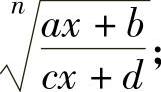
当f(x)中含有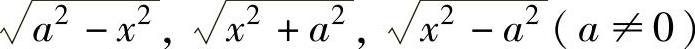 时,分别令x=asint,x=atant,x=asect.
时,分别令x=asint,x=atant,x=asect.
【典型例题】
例2.1.1 求不定积分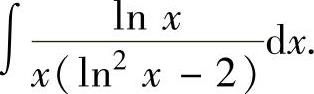
精解 由于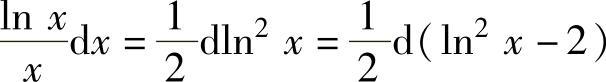 ,所以
,所以
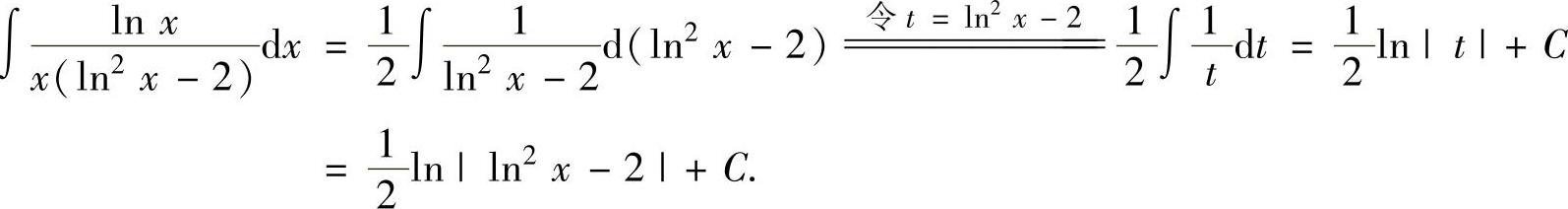
例2.1.2 求不定积分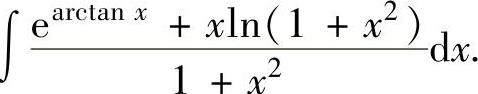
精解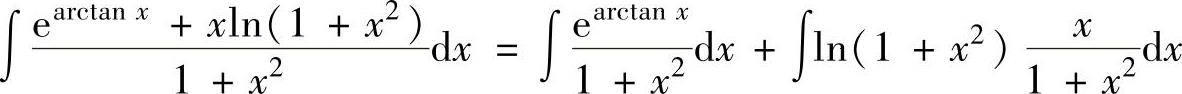 ,(1)
,(1)
其中,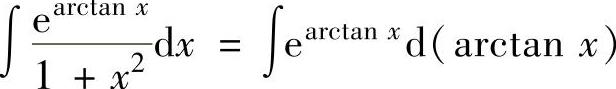
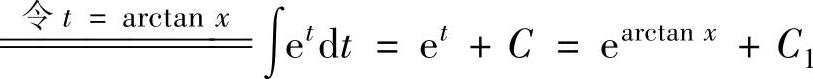 ,
,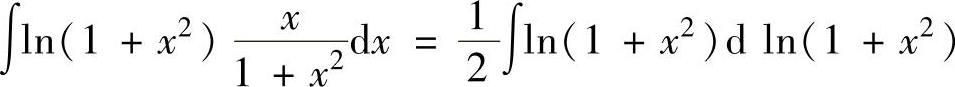
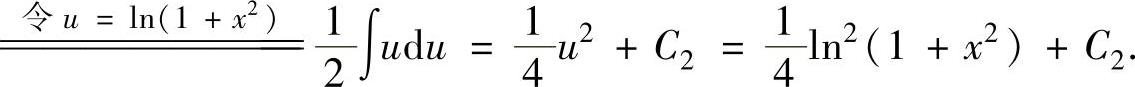
将它们代入式(1)得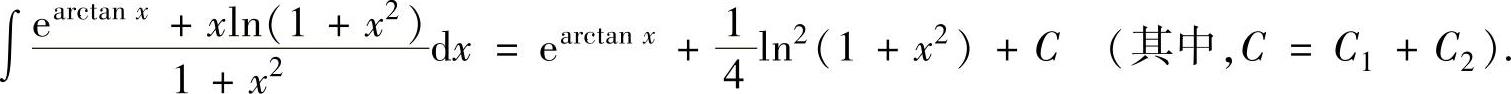
例2.1.3 求不定积分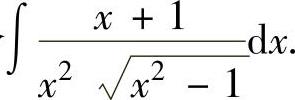
精解 由于被积函数中含有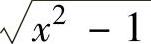 ,所以令x=sect.
,所以令x=sect.
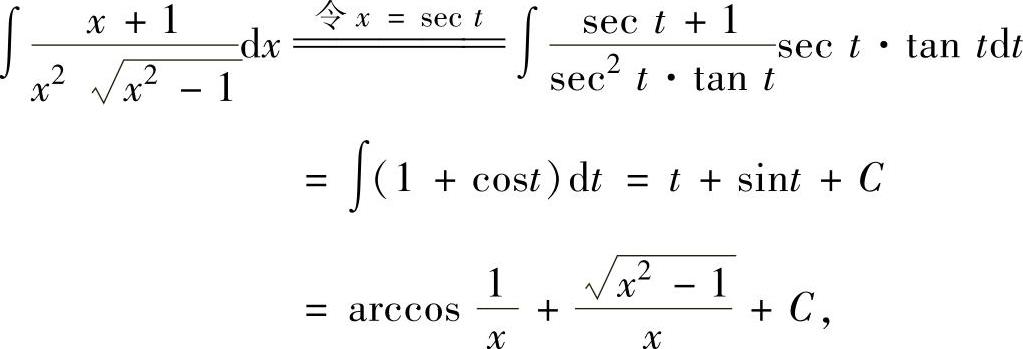
其中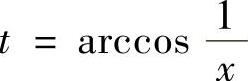 ,
,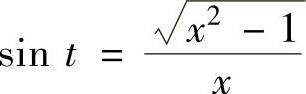 可从图2.1.3得到.
可从图2.1.3得到.
注 由于本题被积函数分母比较复杂,所以也考虑令母中的x这个因子去掉,具体如下: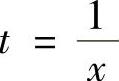 ,将其变得简单些,例如将分
,将其变得简单些,例如将分
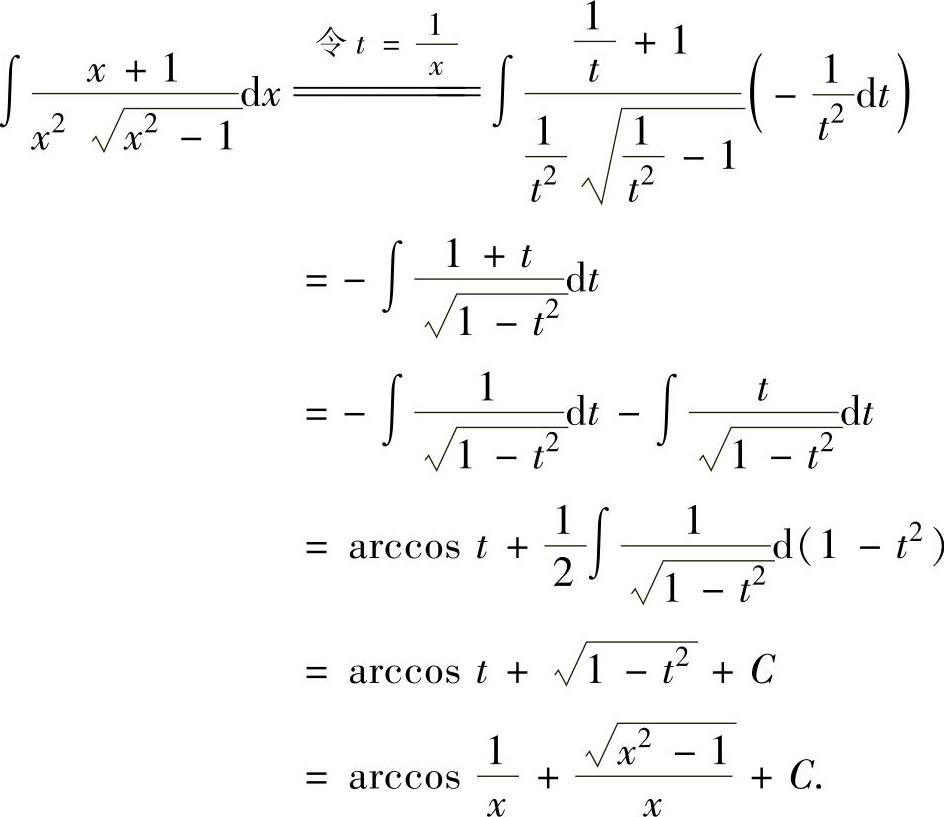
图 2.1.3
例2.1.4 求不定积分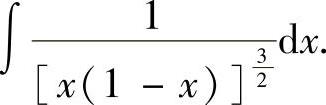
精解 由于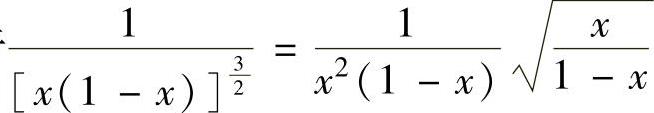 ,即被积函数中含根式
,即被积函数中含根式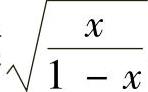 ,所以令
,所以令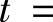
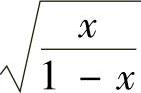 ,即
,即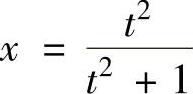 ,于是有
,于是有
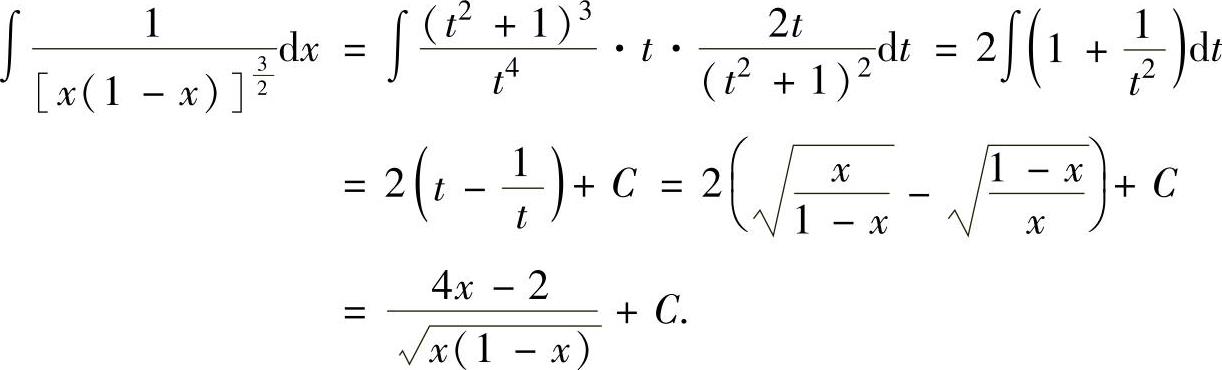
注 本题也可以用如下的变量代换求解:

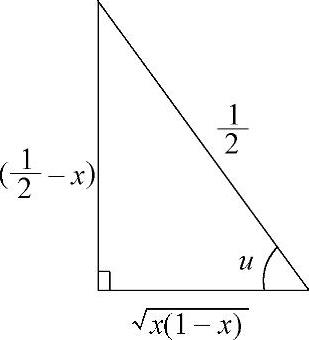
图 2.1.4
例2.1.5 求不定积分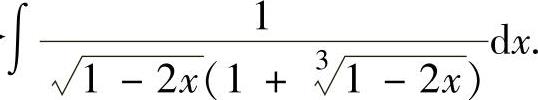
精解 由于被积函数中含有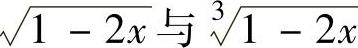 ,所以令
,所以令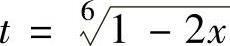 ,即
,即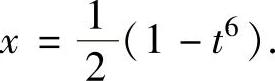
于是有