指标赋权原理
本研究采用“层次分析法”(AHP)为城市软实力各评价指标赋权。层次分析法是美国运筹学家、匹兹堡大学教授T.L.Saaty于20世纪70年代中期提出的。具体实施过程如下。
1.建立递阶层次结构
递阶层次结构的复杂程度与分析问题的详尽程度有关,在每一层次中的元素一般不超过九个。因为太多的元素会给两两比较判别带来困难。
根据上述要求,结合本课题组对城市软实力的定义,城市软实力评价指标体系的层次图如图2所示。
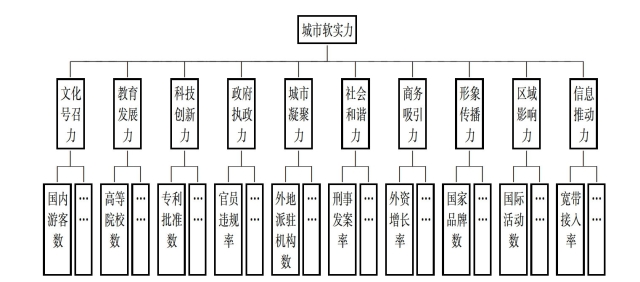
图2 城市软实力评价指标体系层次图
2.构造两两比较判别矩阵
在建立完递阶层次结构后,通过对同一层次的元素进行相对重要性比较,为每一个元素进行赋值,取值范围为1~9,其含义见表2。
表2 判别矩阵元素赋值表
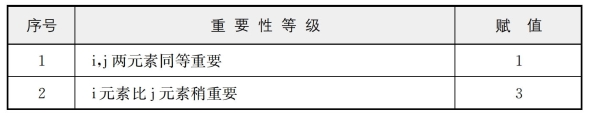
(续表)
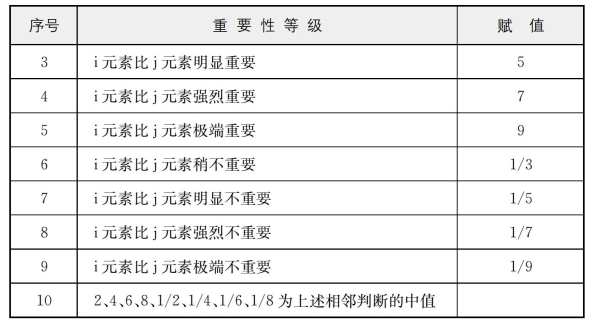
如果i元素比j元素比较相对重要性赋值为ai,j,则j元素比i元素比较相对重要性赋值为1/ai,j。这样得到了两两比较的判别矩阵A:
A=(ai,j)n*n
3.计算各元素的相对权数
利用判别矩阵A=(ai,j)n*n,计算其最大特征根对应的特征向量W,将W正规化后得到各元素的相对权数。具体的计算方式,在不要求特别精确的前提下,可以采用根法、和法等完成。
4.对判别矩阵进行一致性检验
判别矩阵是一致矩阵的充分必要条件是其最大特征根与矩阵的阶数相等,实际计算时,最大特征根与矩阵的阶数不一定相等。可分三步对判别矩阵进行一致性检验。
首先,计算一致性指标CI:
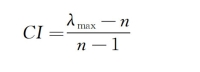
其次,查表得到一致性指标均值RI,一致性指标均值见表3。
表3 一致性指标均值表
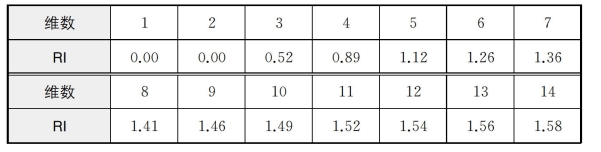
最后,求出随机一致性比率CR:
CR=CI/RI
当CR的值小于0.1时,可以认为判别矩阵具有满意的一致性;否则,就需要调整判别矩阵,使之具有满意的一致性。
5.综合各层次的权数,求出各层次指标对综合指标的权数
利用分层的判别矩阵,可以计算出各个指标相对于上一层的权数,将每一个层次各个指标的权数进行综合,即可得到各个指标在综合指数中的权数,将其代入各个指标的观测值,可以计算出综合评价指数。
