6.1.2 概率抽样的基本原理和抽样分布
我们面对的各种现象，无论是自然现象还是社会现象都可以分为确定性现象和非确定性现象（随机现象）。确定性现象是指在一定条件下必然会发生某种结果的现象。例如，在一个大气压下，纯水在100℃时必然沸腾；在中国传统社会中，婚姻的目的就是为了传宗接代，因此结婚就要生孩子，而且必须生男孩，纳妾或休妻的一个重要原因就是“不孝有三，无后为大”。因此，确定性现象所服从的规律叫做必然规律或肯定性规律，这类现象可以根据已知的事实推算或预测它的结果。
随机现象是在一定条件下可能出现这样的结果，也可能出现那样的结果，但是究竟出现哪种结果事先是不能肯定的。例如，抛掷一枚硬币，事先无法确定是正面向上还是反面向上；结婚后生孩子，孩子的性别事先是无法确定的。
随机现象中的事件在条件实现时，有可能发生也有可能不发生，因此，在一定条件下，可能发生也可能不发生的事件是这个条件下的随机事件。例如，硬币正面向上是抛掷硬币这个条件下的随机事件；生育女孩是结婚生孩子这个条件下的随机事件。与此对应，确定性现象中的事件就是必然事件，即在一定条件下必然发生的事件是这个条件下的必然事件。
社会研究中的社会现象大多是随机事件，很少有必然事件。从表面上看，随机事件好像捉摸不定，纯粹是偶然性在起支配作用，很难预测现象的结果。其实不然，在研究了大量同类的随机现象后，通常会发现一种确定的规律性，即在各种随机事件背后，存在着事件发生的客观概率。
曾经进行过的抛掷硬币的实验发现了硬币“正面向上”这一事件发生的规律。三位实验者分别抛掷硬币4040次、12000次、24000次，其中正面向上的次数分别为2048次、6019次、12012次，频率分别为0.5069， 0.5016， 0.5005。根据一项利用电子计算机进行的模拟试验，观察“由0， 1， 2， …9中任意取出一个数字”的随机试验中，事件为“取出的数字是1”发生的规律。在10组2000次的观察中， “ 1”出现的频率由低到高分别为0.0915 ， 0.0925， 0.0970，0.1015， 0.1020， 0.1020， 0.1025， 0.1025， 0.1090， 0.1060（严士建，王巂骧，徐承彝， 1982： 2-3） 。
由此可以看出，在多次反复试验中，同一事件发生的频率虽然并不完全相同，但却在一个固定的数值附近摆动，并且呈现一定的稳定性，抛掷硬币正面向上的频率是围绕0.5摆动，并且抛掷次数越多，频率摆动幅度越小；计算机模拟实验的结果发现，出现“1”的频率是围绕0.10摆动。
所谓概率就是事件发生频率所接近的固定数值，它是相应事件发生的可能性大小的一个客观、定量的度量。因此，频率的稳定性，揭示出一个随机事件发生的可能性的大小。频率稳定于较大数值，表明相应事件发生的可能性较大；反之，则表明相应事件发生的可能性较小。
上述现象就是概率论中的“大数定律”，又称为“大数法则”或“平均法则”，是概率论的主要法则之一。它的意义是：在随机事件的大量重复出现中，往往呈现几乎必然的规律，这类规律就是大数法则。通俗地说，这个定律就是，在试验条件不变的情况下，重复试验多次，随机事件的频率近似于它的概率。例如，乘飞机旅行，个人出事的概率是未知的，对个人来说，安全与事故具有随机性。但是对每年100万人次所有乘飞机的旅行者来说，如果将100万人理解为100万次的重复试验，其中，总有20人死于飞行事故。那么根据大数定律，乘飞机出事故的概率大约为十万分之二。
因此，抽样所依据的原理是概率论中的大数定律。就是说，事物总体中的每一单位都有均等的机会被抽取，即等概率抽样，这是概率抽样最重要的原则。按随机原则从事物总体中抽取的每一个样本单位的数值，对于总体的平均数来说，可能大，也可能小，而抽样数目越多，样本平均数越接近总体平均数。
例如，对于1000名全部由女生组成的总体，出现事件为“女”的概率永远等于1，对于1000名由男女生组成的总体来说（其中男生400名，女生600名），出现事件为“女”的实际概率应该是0.6。如果抽取10组100人的样本，并且严格按照等概率的原则抽样，则出现事件为“女”的频率会围绕0.6左右摆动；如果在1000人中抽取5组分别为100人、200人、300人、400人、500人的样本，出现事件为“女”的频率稳定性是不一样的，样本人数越多，出现事件为“女”的频率越是接近0.6。这就涉及抽样原理的第二个问题，即抽样分布。抽样分布表示在一个既定的总体中不断抽取样本时，各种可能出现的样本统计值的分布情况。因此，抽样分布是根据概率原则而成立的理性分布。
对于随机现象来说，变量取值上的次数分配就是概率分布。例如，生男生女是随机现象，性别变量的取值“男”或“女”就是两个随机事件。如果100个新生儿中“男”事件的出现次数为55、 “女”事件出现次数为45，则男婴的概率为0.55，女婴的概率为0.45，这两项概率就是性别这一变量的概率分布。
抽样分布的变化与样本容量有关。当样本容量持续扩大时，在同一总体中抽取的m组样本的平均值范围逐步缩小，出现相同平均数的数量会相应增加，所有样本的平均值分布呈现出向总体平均数集中的趋势。例如，对于一个由10个孩子组成的总体，他们的年龄从1岁到10岁，平均年龄为5.5岁。从中可以分别抽取出m组1， 2， 3， …10人组成的样本。若从中抽取1人作为样本来估计总体平均值，显然，全部可能的“10”组样本所得到的估计值区间是1～10岁；若从中抽取2人作为样本，根据排列组合公式
可以抽取45组不同的样本，根据全部样本平均值所得到的估计值区间为1.5～9.5岁，并会出现不少相同的平均数，如1岁和9岁、2岁和8岁、3岁和7岁、4岁和6岁，4组样本的平均年龄都是5岁；同理，若从10人分别抽取3人或4人或5人组成的样本，根据排列组合公式，分别可以抽取120组、210组、252组样本，根据全部样本平均值所得到估计值区间分别为2.0～9.0岁、2.5～8.5岁、3.0～8.0岁，并且相同样本平均值的数量也随着样本容量的扩大而增加。这种抽样分布即为均值抽样分布。
根据中央极限定理，在一个含有N个单位并且均值为µ、标准差为σ的总体中，抽取所有可能的含有n个单位的m组样本组合，样本平均值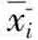
的分布是一个随着样本数n越大而越趋向于由均值µ和标准误
组成的正态分布（见图6-2） ；并且当n足够大时（n≥30） ，无论总体的分布如何，样本平均值所构成的分布都趋于正态分布。正态分布的曲线呈钟型，具有单峰和对称的特点，因此，在正态分布中，众数、中位数和均值是相同的；正态分布曲线两端逐渐降低，但不会接触底线，即x值与均值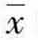
的差异越大，其次数就越少，但不会等于零；正态分布曲线下的全部面积恒等于1。
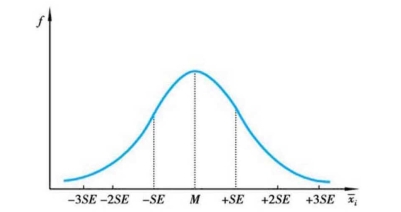
图6-2 均值正态分布
在正态分布中，所有m组样本组合的均值的平均数等于总体的平均值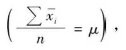
所有m组样本组合的平均值的标准差，即为标准误（SE） ，它等于总体标准差除以， 即：
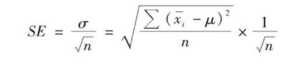
在抽样分布呈正态分布的条件下，其平均数的次数所占的比率就是正态曲线下的面积。按照概率统计理论，正态分布曲线下的任何面积是可以计算的。例如，有68.26%的样本平均值是落在µ±SE的区间内，有95.44%的样本平均值是落在µ±2SE的区间内，有99.73%的样本平均值是落在µ±3SE的区间内。但在实际的统计推论（参数估计）中，经常采用的置信度是90%，95%， 98%， 99%，与此相应的区间范围是（其中的数字即z值，即标准分数，可以从正态曲线下的面积表查找）：
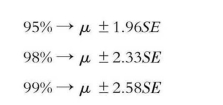
上述数字实际上就是参数估计中的置信度（90%， 95%等）和置信区间（µ±SE等），它们的大小对于样本规模的确定和统计推论具有重要意义。
抽样分布的另一种形式是二项分布。二项是指变量的取值只有两个，例如性别的取值有男和女，婚姻状况的取值有已婚和未婚，对某种意见的态度有同意和反对。二项中的一项概率为p，另一项的概率即1 -p，设为q。假定某大学男女学生各占一半，则男女的概率均为0.5，即p（m）=0.5， q （w）=0.5。若在该大学中任意抽取1， 2，3…n人，抽取男生和女生的可能性将如何？
若抽取1人，则有两种可能：p=0.5（男）， q=0.5（女）。
若抽取2人，则有三种可能：2男、1男1女、2女，出现的概率分别为0.25， 0.50， 0.25。
若抽取3人，则有四种可能：3男、2男1女、2女1男、3女，出现的概率分别为0.125， 0.375， 0.375， 0.125。
若抽取更多的学生，概率分布就比较复杂。二项分布和代数中的二项式是一致的。二项式（a+b ）n中的a与b分别改为p与q即可。代入二项式并展开：
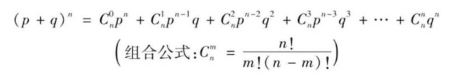
二项分布也可以计算一组特殊样本被抽取的概率以及对统计推论的意义。例如，假定某大学男女生的比率是一样的，都各占50%，如果从该大学中抽取一个由10人组成的样本，并要求该样本中有3～7人是男生，该样本被抽取的概率根据上述公式计算如下：
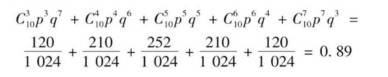
计算结果表明，若要抽取含有3～7位男生的10人一组样本的可能性为89%；也可以说，如果我们抽取100组10人一组的样本，那么将有89组的样本中男生的人数在3～7人。
但是，若要抽取10人全部是男生的样本，由于该大学男女生的比率是一样的，即p=q=0.5，如果严格按照概率抽样的原则，这样的样本被抽取的可能性极小，即
最多只有1‰的概率。所以一般是不会被抽到的，是小概率事件。如果被抽到的话，就存在两种可能：一是没有按照概率抽样的方法抽取样本；二是我们原先对这所大学男女生各占一半的假定是错误的。概率分布的这一意义构成了统计推论的基础之一，即小概率事件的发生，对假设鉴定具有重要意义。
从二项分布的图形来看，当p=q时，两项分配是对称的。但是当p≠ q时，二项分布是偏态的，但是当n趋向于无限时，p≠q的二项分布也趋向于对称。例如，若我们抽取许多组由100位学生组成的样本了解他们的 性别，可以发现有更多的样本会产生相同的估计值，形成如图6-3显示的正态分布曲线图。
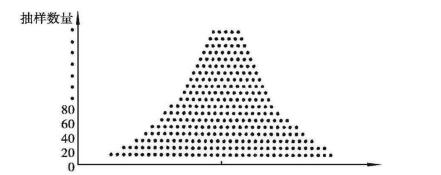
图6-3 二项分布
因此，概括地说概率抽样具有以下特点：第一，从总体中抽取出来作为调查的样本单位是按随机原则抽取的，是不得任意选择的。因此，能够被抽中的单位在总体中呈均匀分布，对总体具有充分的代表性，不致出现倾向性误差。第二，它是以抽取的全部样本单位来代表总体，而不是用个别单位来代表总体。因此，抽样调查的结果只能推论到样本所在的总体，不能用样本单位的个别特征来说明总体特征，更不能把样本的特征推论到总体之外的社会现象。当样本数足够多时，个别单位的高低差异趋于互相抵消，因而样本的平均数接近总体平均数。第三，抽样误差和总体各单位或元素之间的差异程度成正比，与样本规模成反比。但是，抽样误差可以根据总体中各单位或元素的差异程度与样本规模，控制在一定的范围内。因此，抽样调查是非全面调查方法中用来推论总体的最完善、最有科学根据的方法。