6.2.8 样本规模和抽样方案
抽样调查中人们最为关注的是样本大小的确定。有的调查只有一百多人，甚至更少，有的有几万人，大多数抽样调查的样本是几千人。那么在社会学研究中，一项抽样调查到底需要多大的样本规模呢？
6.2.8.1 样本规模的估计
样本规模的大小涉及总体的状况、抽样调查结果对总体推论的要求、研究课题的复杂性以及调查经费的多少等各种因素。但是从抽样原理或抽样分布来说，样本规模不能少于30个单位或元素。在统计学中，一般把大于30个单位或元素的样本称为大样本，小于30个的样本称为小样本。以30为界区分大样本和小样本，并不是说30个样本对于抽样调查已经足够大了，而是指只有在至少满足30个样本要求的条件下，它的平均值的分布才能接近正态分布。
因此，在调查研究中30个样本是远远不够的。对于样本大小的确定，有两种方法。一种是经验估计法。根据笔者征询有关专家的意见，不少专家认为，在调查研究中，一项比较规范的研究（能够达到对较大总体的统计推论），样本规模至少要在500个以上。因为，当社会从传统转向现代时，总体的复杂性是以往社会不能比拟的；社会统计方法越来越先进，采用多元回归分析方法已经是现代社会调查分析资料的常用方法；同时，抽样调查的重要作用是要在一定的置信度要求下推论总体。虽然有些学者认为，抽样调查的样本规模最低数量不得少于100个，但这仅是对简单统计分析方法而言。要能够运用多元回归分析方法甚至更先进的方法，100个样本还是不够的。当然，考虑到经费、时间和人员的效率，样本规模也不是越大越好。
确定样本大小的第二种方法，也是最常用的，是根据样本规模的计算公式，得出所需要的样本数。对于样本规模的计算，严格地说，不同的抽样方法，计算公式是不一样的，但是它们的基本原理是一样的，都是建立在简单随机抽样计算方法的基础上。本章仅介绍简单随机抽样公式的计算方法。
简单随机抽样样本规模计算公式是根据推论总体均值的原理而推导出来的。样本规模计算公式为：例如，在一个班级中，如果有一半是女生，一半是男生，说明在性别上，这个班级的差别是最大的；反过来如果全部是男生或女生，说明这个班级在性别上是完全一致的，是没有差异的。因此，p值为0.5时，一方面假设了总体的异质性为最大，适合所有总体的情况，不管它的差异程度有多大，同时也可以进一步简化计算公式，当把p=0.5代入公式时，上述公式就成为：
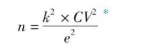
*有些教材的计算公式是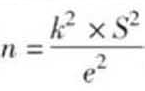
，其中标准差（s）是绝对值，其他值都是相对值，不符合计算原理。
其中，k为置信度系数，即置信度所对应的临界值；CV为总体相对标准差或离散系数；e为抽样误差。其中置信度反映的是推论总体的把握度或可信度，k值即为置信度系数，可以在标准正态分布表上查到；总体标准差反映的是总体元素之间的差异程度（简称总体差异性），是要经过对总体的调查才能 获得的，因此是未知的；抽样误差即为总体参数值和样本统计值的偏差值，是可以事先规定的。为了解决CV值即总体相对标准差或离散系数不可能或不容易获得的问题，根据推论总体比例或百分比的原理，计算公式可以改写为：
其中，p为总体百分比。一般来说，当p值等于0.5时意味着总体差异为最大。
在具体抽样时，只要事先确定k值和e值就可以得到所需要的样本数。例如，一项抽样调查事先要求置信度为98%，查表得知，它的对应值，即k值为2.33，抽样误差控制在3%，即e值为0.03。代入公式可知，在这样的条件下样本人数为1508人，并且适合总体差异最大的条件。为了方便抽样，根据最常用的k值，即在95%的置信度下（k=1.96 ） ，按照上述公式计算可以得到不同抽样误差下的样本规模（见表6-5） ，可以发现，在同等置信度条件下，抽样误差越小，样本数量就越大。如果采用多段抽样方法，根据简单随机抽样公式计算获得的样本量还要乘以复合抽样的设计效应系数（Deff）进行修正。根据一些专家抽样经验，我国的Deff一般为2.5。如果上例采用多段抽样调查方法，还必须乘以2.5，即1508×2.5=3770人。
但是，上述计算公式不能适用于总体是一个特定的组织且规模比较小的情况。在有些抽样调查中，总体是一个界限分明的组织或群体，如某个企业、学校等，此时样本数通常应占总体数的5%以上。根据样本数量和总体规模之间的关系（见图6-6） ，可以发现当总体规模较小时，样本数量所占的比率较大。另外，样本规模最好在500人或以上。在这样的有限总体的条件下，样本大小不受限制。有限总体中样本规模的计算公式与无限总体差不多，不过增了总体单位数的变量：
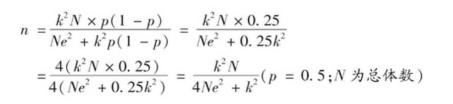
例如，一项抽样调查事先要求的置信度为98%，查表得知，它的对应值，即k值为2.33，抽样误差控制在3%，即e值为0.03，总体规模N=10000。代入公式可知，要满足上述k值和e值，样本数为1310人。有限总体样本规模计算公式比较适合于总体规模较小以及对于置信度和抽样误差有比较高的要求。例如，当k值和e值与上例一样，N=500时，样本规模为375人，当N=1000时，样本规模为601人；当N=2000时，样本规模为860人。如果按无限总体的样本规模计算公式，样本规模本身就要大于总体规模或接近总体规模。即使降低对置信度和抽样误差的要求，情况也差不多（见表6-5） 。由于有限总体比较容易获得有关反映总体相对标准差或离散系数的资料，如果能够得到这些资料，则可以取代p（1-p）。例如，当总体职工收入相对标准差为0.25时，总体数为1000人，其他条件不变，根据计算公式：
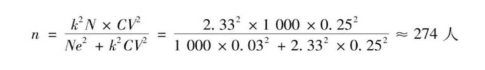
之所以比原来的样本数量要少300多人，是因为总体的差异性大大下降。
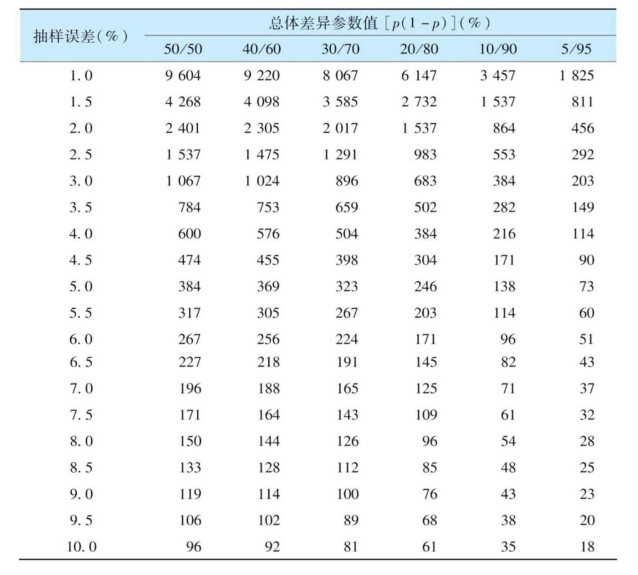
表6-5 在95%置信度、不同抽样误差和总体差异性条件下必须达到的样本规模
6.2.8.2 影响样本规模的因素
从以上的计算公式可以发现影响样本规模的因素主要是总体规模的大小、总体的差异性、抽样误差以及推论的置信度。除此以外，影响样本大小的还有抽样方法、经费、时间和人力。
（1）总体规模。一般而言，总体规模越大，样本也越大，但是根据有限总体抽样公式计算的结果，当总体达到一定规模以后，样本量的增加并不与总体规模的增加保持相同的速率（参见图6-6） ；也就是说，在相同条件下，当总体达到一定规模后，样本量的增加与总体规模的增加并不成正比。例如，置信度为95% （K=1.96） ，抽样误差为0.03，总体500人，样本数是340人，总体数若按50%的比率增加，分别为750人，1125人，1688人，2531人，样本数分别为440人，548人，654人，751人，分别增加29.4%， 24.5%，19.3%， 14.8%。因此，在一个趋向无限大的总体中，样本的增加是有限的。这一规律告诉我们，一个10万人的总体和一个100万人乃至更大的总体，在其他条件一样的情况下，样本量的变化并不会很大。
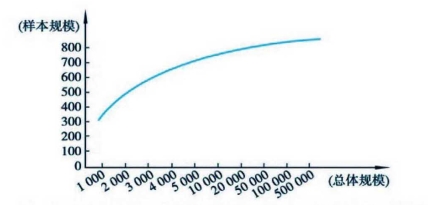
图6-6 总体规模和样本数量
注：在95%的置信度、 ±3置信区间和总体参数值为50%对50%的条件下。（资料来源：林南，1987： 182）
（2）总体差异性。总体差异性如前面所讲的是指总体单位或元素之间的差异程度。总体单位或元素之间的差异越大，也就意味着它的同质性程度越低或者异质性越高。根据前例可以发现，在其他条件不变的情况下，样本规模与总体的差异性是正比关系，即总体差异性越大或异质性程度越高，样本的规模也越大。在抽样公式中，总体相对标准差或总体成数（百分比）是反映总体差异性的指标。例如，在一个同质性程度很高的总体中（总体差异参数值5%对95%） ，抽样误差为0.03，样本数为203人，但是在一个同质性程度较低的总体中（总体差异参数值40%对60%） ，样本数为1024人（参见表6-5） 。
（3）抽样误差和可信度。由样本计算公式可知，置信度与样本规模是正比关系，即置信度越高，样本量就越大；事先规定的抽样误差越小，样本量就越大。在相同的置信度条件下，抽样误差越小，样本规模就越大（见表6-5） 。例如，在95%的置信度条件下，当抽样误差控制在5%水平时，样本量为384人，当抽样误差控制在4%水平时，样本量为600人，增加了216人，但是当抽样误差精确到1%时，样本量为9604人。在有限总体中，随着抽样误差的缩小，样本量也会急剧增加。例如，总体为2万人，置信度为95%，抽样误差为5%时，样本量为377人；抽样误差为4%时，样本量为583人；当抽样误差为1%时，样本量为6488人，差不多要占总体数的1/3。美国华裔学者林南在《社会研究方法》教材中应用了类似的资料说明这个问题（林南，1987： 183） 。毫无疑问，在相同的条件下，置信度的高低也会对样本规模产生影响，以无限总体为例，在相同的抽样误差下，如0.03，当置信度为98%时，样本量为1508人；如果置信度降低为95%，样本量为1067人；当置信度降低为90%时，样本量为756人。
（4）经费、人力和时间。经费、人力和时间合在一起就是调查成本，在所有的条件中起关键作用的还是经费，抽样调查是成本比较高的一种研究，无论抽样做得如何精细，样本有多大，推论的可信度和精确度有多高，没有经费都是纸上谈兵。现在，一份问卷的调查成本为50～100元，有时甚至更多。因此，没有足够的经费是不能进行抽样调查的。经费不管多少总是有限的，但是对于抽样的要求是无限的，因此我们只能在有限的经费条件下，尽可能达到比较高的可信度和精确度。除此之外，还要考虑时间和人力因素。因为，完成一个规模比较大的样本调查，需要比较长的时间和比较多的人参加。
（5）抽样方法。根据前面介绍的五种基本的抽样方法，即简单随机抽样方法、系统抽样方法、分层抽样方法、整群抽样方法和多段抽样方法，在同等条件下，采用不同的抽样方法获得样本对总体的代表性程度会有差异。大致来说，分层抽样抽取的样本对总体的代表性程度最高，其次是通过简单随机抽样方法和系统抽样方法抽取的样本，代表性程度最低的是通过整群抽样方法和多段抽样方法抽取的样本。因此，对于一项抽样调查，如果选择整群抽样方法或多段抽样方法，要在“标准的”样本数量（通过上述公式计算后得到的样本数量）基础上适当增加一些样本，即用简单随机抽样公式计算获得的样本量乘以复合抽样的设计效应系数（Deff） 。
由于影响最大的是经费和推论所要求的精确性和可信度，因此，最佳样本需要满足以下条件：在规定的经费范围内达到最高的可信度和精确性；或者以最少的费用达到规定的可信度和精确性。
6.2.8.3 抽样方案设计
调查研究方案中必须包括抽样方案设计。抽样方案主要是为了指导具体的抽样，它不仅包括抽样方法的选择，还包括总体和调查对象的界定、调查时间和调查周期的安排、样本规模的大小、抽样的可信度和精确度等。根据国内大型抽样调查的实践，抽样方案主要包括以下几个方面：
（1）说明抽样调查目的。例如，中国人民大学主持的《中国综合社会调查（CGSS）》的调查目的或宗旨是：“定期、系统地收集社会各个方面的数据；通过收集追踪性数据，总结社会变迁的长期趋势”，等等。
（2）抽样的组织方式。在全国性的、大规模的抽样中，必须建立相应的组织方式，确定抽样的组织机构，例如，负责和实施抽样的具体组织、参加人员等；抽样完成的具体时间；抽样结果的上报程序和检查抽样质量的具体安排等。
（3）对总体、调查对象和调查时间的说明。在抽样方案中必须对总体进行严格、详细的说明，规定调查对象的具体标准以及实施抽样和抽样调查的具体时间。例如，2001年中国当代社会结构全国调查的总体和调查对象就规定为：2001年全国除西藏和台湾以外的年龄在16～70岁的常住居民人口；城镇人口与农村人口作为两个独立的总体，并以非农户口和农业户口作为区分两个总体的具体标准。由于各参与单位具有自己的特殊情况，对于抽样的实施时间和调查时间未作统一规定，但是要求调查必须在2002年全部完成。
（4）对抽样方法的详细说明，其中包括抽样原则或方法，样本大小及其置信度，抽样误差和对总体差异程度的估计，以及具体的抽样步骤。例如，2001年中国当代社会结构全国调查就规定具体的抽样方法是“分层、分域、多阶段混合抽样”，分为五级抽样：省、自治区、直辖市阶段采用分层比例抽样；市、县阶段采用分域和PPS抽样方法；居委会或村委会阶段采用PPS抽样方法；居民户阶段采取等距抽样方法；入户抽样采取“生日法”或简单随机抽样。对于样本规模的计算采用简单随机抽样方法的计算公式，并规定置信度为95%，总体差异性为0.5，抽样误差为3%，由此估计各地的样本量，并且规定了每级抽样单位的样本数。
全国性、大规模的抽样调查大多采用多段抽样方法或PPS抽样方法，因此还要规定：具体的抽样步骤；每一阶段实施抽样的负责单位或个人；各参与单位必须提供抽样需要的具体资料，尤其是各阶段抽样的抽样框资料。例如，2001年中国当代社会结构全国抽样调查中，从第一级（阶段）抽样到第三级（阶段）抽样主要由研究主持单位负责实施，根据各参与单位提供的所在省市的抽样框资料，直接抽取到居委会或村委会，并规定各居委会或村委会具体的调查人数；然后把抽样结果发到各参与单位后，根据各参与单位反馈的意见进行适当调整。各参与单位主要负责最后两个阶段的抽样，即在被抽取的居委会或村委会中抽取居民户，再在居民户中抽取调查对象。
（5）可能存在的问题及控制。任何抽样方案都不可能是非常周密的，都会与实际情况发生矛盾，因此还要根据可能发生的实际问题规定具体的解决办法。例如，在我国城乡最可能发生的“人户分离”，以及现场控制等。此外，还有具体抽样的督查和最后样本质量的检查和控制；实际调查对象和样本名单的控制，以及样本构成和访问质量之间的关系，等等。