7.5.4　定比测量

定比测量不仅包括了定类、定序、定距三种测量的数学特征（=、≠；＞、＜；+、-），而且还可以进行乘除运算。因此，定比测量也称为等比测量或比率测量。定比测量的一个最大特点是它有一个绝对的零。例如，某年上海的年人均收入是4万元，全国的人均年收入是2万元，我们既可以说上海年人均收入要比全国年人均收入高2万元，也可以说，上海年人均收入是全国的2倍。在社会测量中，经常使用的属于定比测量的变量有年龄、收入、出生率、死亡率、离婚率、性别比、人口密度等。

根据以上分析，测量层次具有以下几个特征和意义：

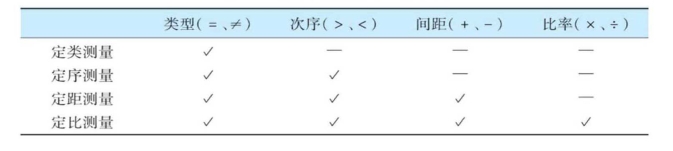
第一，从定类测量到定比测量是一个递进过程，也就是说测量层次比较高的变量同时具有测量层次比较低的所有属性。例如，定比测量所具有的属性是等于和不等于、大于和小于、加减乘除运算；定距测量具有的属性是等于和不等于、大于和小于、加减运算；定序测量所具有的属性是等于和不等于、大于和小于（见表7-1） 。

第二，由于测量层次比较高的变量同时具有测量层次比较低的所有属性，因而测量层次比较高的变量可以转换为测量层次比较低的变量。例如，年龄根据出生年份的计算属于定比测量，但是在社会测量中可以根据需要转换为定距的、定序的，甚至是定类的（如“文化大革命”前出生和“文化大革命”后出生）。但是，测量层次低的变量不能转换成测量层次高的变量。需要注意的是，除了特殊需要以外，我们尽可能不要把测量层次高的变量转换为测量层次低的变量，因为测量层次高的变量所含有的信息更多，更能采用数学运算的方法分析。

第三，判断变量所属的测量层次，最为重要的是可以帮助我们选择适合变量测量层次的计算方法，尤其是在初级和中级统计中，对于哪种测量层次的变量应该采用什么样的统计方法都有严格的规定。一个基本的标准是：凡是适合于测量层次比较低的变量的统计方法，也可以用于测量层次比较高的变量的计算；反之，则不行。例如，可以用平均数计算年龄（平均年龄），但是不能用平均数计算性别，不能说一个班级的平均性别是什么；但可以说班级里多数是女生（众数），也可以说班级里多数学生的年龄在20岁左右。众数适合于定类测量及以上层次，平均数仅适合于定比测量。

第四，虽然定类测量和定序测量的变量不能采用数学性质较高的方法计算，但是并不意味这些测量类型的变量就不能进行统计了。这些类型的变量可以作频数统计、比率计算，例如，一个班级中男女学生的比率或人数，性别比等，以及适合于这些类型变量的简单的相关统计方法。随着统计技术的发展，原来不能对定类或定序测量变量进行多元回归统计的，现在也可以采用“虚拟变量”的方法进行多元回归统计分析或者多元对数回归统计分析。