10.2.6 拉丁方格设计
随机区集设计只能控制一个外来变量对实验的影响,拉丁方格设计可以控制两个外来变量的影响。前面的例子都假定三个建筑工地的民工是同质的,但是建筑公司的规模有大有小,有的管理规范,经常为农民工提供教育培训,有的管理很差,除了生产其他都不管。因此,我们希望控制的外来变量是城市(区域)和建筑公司(实验单位)。在拉丁方格设计中,实验变量、实验单位和区域的数量必须相等,经过排列组合,实验单位可以分配到三种实验变量。如果实验单位有三种,就会形成3×3的方格,所以称为拉丁方格设计。
拉丁方格设计中比较关键的是按随机方法分配实验变量,如果实验变量有三种(a、 b、 c ) ,实验变量的随机分配方法和步骤如下。①给实验变量编号:1=a、 2=b、 3=c。②行处理,按随机方法决定三个实验变量的位置。假如第一次随机抽到的数字是2、 3、 1,即第一行各列的三个实验变量顺序为b、c、 a;第二行的随机数字是3、1、2,即第二行各列的三个实验变量顺序是c、a、b;第一行和第二行的变量顺序安排好了,第三行各列的三个实验变量的顺序自然是a、b、c,形成3×3的方格x(见表10-10中x)。 ③列处理,将调整好的方格x中的第一列b、 c、a分别用1、 2、 3表示,按随机方法抽出如1、3、2,安排新拉丁方格第一列各行的实验变量,即b、 a、 c;用同样方法抽取如2、 1、 3三个号码,第二列各行的实验变量顺序是c、b、a;第三列各行的实验变量顺序自然是a、c、b,形成新的3×3方格y(见表10-10中y) 。④最后把拉丁方格列处理(y)后的实验变量分配到三个实验单位和三个区域(见表10-11)。
按上例,我们分别在北京、上海、广州3个城市中每个城市选择三个工地A、B、 C进行实验研究,实验变量仍然是图片展示(a) 、看录像(b) 、个别访问或辅导(c),经过测试获得60分及以上的人数分布如下(见表10-12) 。从图中看出,拉丁方格设计中每个城市的每个工地只能采用一种实验方法,但是在不同城市的同类工地采用的实验方法又是不同的:
表10-10 实验变量行处理和列处理

表10-11 拉丁方格设计实验模式
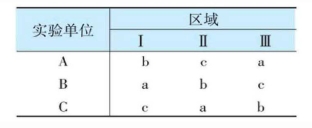
表10-12 拉丁方格设计实验举例
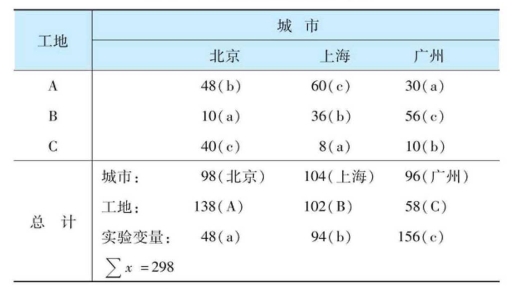
注:表中数字为获得60分及以上的人数分布。
最后按照方差分析方法进行假设检验(F检验),与随机区集设计比较,拉丁方格设计的实验结果要进行三类方差分析,即实验变量、区域、实验单位方差分析。经计算,![]()
![]() 也就是说,实验变量在显著水平为0.10的条件下有一定差异,不同工地或城市的差异很小或几乎没有差异。
也就是说,实验变量在显著水平为0.10的条件下有一定差异,不同工地或城市的差异很小或几乎没有差异。
