附录A 抽样方案示例
中国社会变迁调查抽样方案[1]
沈崇麟
一、抽样方案与样本量的确定
中国沿海发达地区社会变迁调查的总体为沿海18个城市（大连、青岛、烟台、天津、秦皇岛、连云港、南通、上海、宁波、温州、福州、厦门、汕头、广州、深圳、珠海、湛江和北海）的市辖区中的20～65岁常住人口。抽样方案采用分层5阶抽样。前4阶市、区、街道（镇）和居（村）委会样本单位的抽取，采用与样本规模成比例的不等概率放回抽样，即PPS抽样法，在居委会中采用等距（系统）抽样方法抽取家庭户，在家庭户中随机抽取一个20～65岁的调查对象。调查的样本容量为3000。
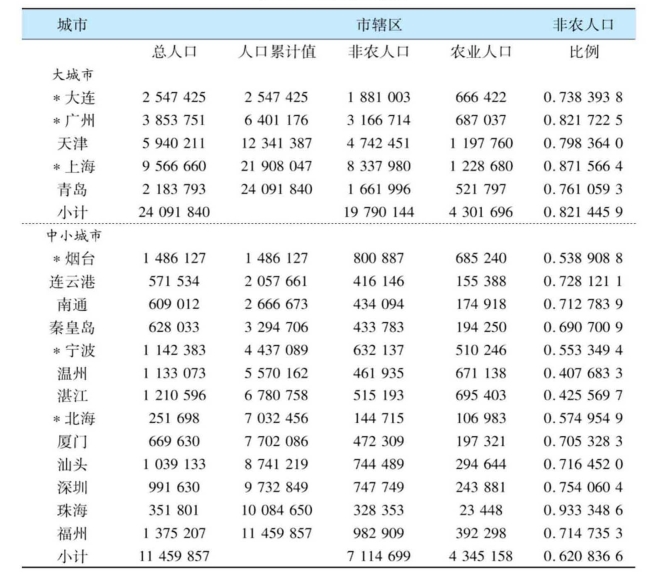
抽样的第一阶，我们将这18个城市作为初级抽样单位，按城市规模分为二层，其中市辖区人口在200万以上的为大城市层，计有上海、天津、青岛、大连和广州五个城市；市辖区人口在200万以下者为中小城市层，计有烟台、秦皇岛、连云港、南通、宁波、温州、福州、厦门、汕头、深圳、湛江、珠海和北海共13个城市。在分层以后，我们用PPS法，分别从已分好的二层中各抽取3个城市，被抽取的城市分别为上海、大连、广州（大城市层）和烟台、宁波、北海（中小小城市层）。抽样结果见表A-1。
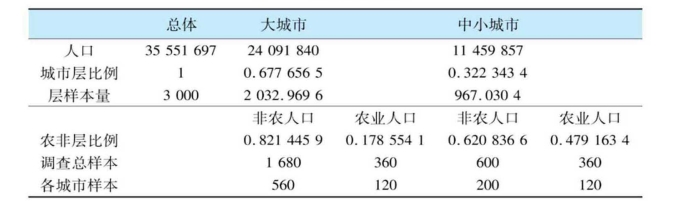
根据二层中的人口在总人口中所占比例0.68和0.32（见表A-2） ，确定二层的样本量，二层的样本量分别为3000 × 0.68=2040和3000 × 0.32=960。在确定层样本量后，采用层内样本城市等样本量分配的原则，分配给各层的每一城市的样本量分别是，大城市层，大连、上海和广州的样本量均为2040/3=680，中小城市层，烟台、宁波和北海的样本量均为960/3=320（见表A-2） 。
抽样的第二阶，分别在各样本城市中抽取区。首先将所有样本城市中的行政区根据非农人口比例分为二层。非农人口比例高于85%（含85%）的区归入城区层，否则，则归入城乡结合区，即城郊区层。为保证在层内各个样本市中，农业与非农样本比例不至于差别过大，在确定城市中农业与非农样本比例时，我们没有使用样本市本身的农业与非农人口的比例。而使用了城市所在的层的农业与非农人口的比例。之所以这样做，是因为此项目研究分析的总体是沿海地区大城市层、中小城市层以及沿海18个城市，各个城市不进行总体推论，各个城市农业与非农样本使用同一分配比例，使样本量的分配和调查实施简单化。如果某一城市需要进行总体推断，可以根据本市农业与非农人口的比例（见表A-1 ） ，对样本进行加权处理。
表A-1 分层城市抽样
注：“①”为抽中的城市；人口统计数据来源于《全国分县市人口统计资料——1995年度》，中华人民共和国公安部编，中国人民公安大学出版社，1996年。以下表格数据同一来源。
表A-2 各层样本量分配
完成了城市中农业与非农的分层后，分别在各个样本城市的城区和城郊区用PPS法抽出样本区。
抽样的第三、四阶，首先收集样本区1995年的区、办事处（镇）和居委会（村）的人口资料，这些资料要包括每区的区、办事处和居委会的分性别、年龄和分农业和非农人口的统计资料。利用这些人口资料采用PPS法抽出样本办事处（乡镇）和样本居（村）委会。办事处（乡镇）和居（村）委会的样本等量分配。
以上第一至第四阶的抽样由项目课题组完成，抽样的结果，各阶样本单位的编码、名称和样本量的清单见附录。
第五阶抽样由各个城市的调查组完成，收集样本居委会所有户籍资料，列出抽样框。根据抽样清单中的各居委会的样本量，用等距（系统）抽样法抽出被调查户。在调查户中，以20～65岁，生日最接近7月1日的人为调查对象。
为了不至于因为调查对象不在场或不能回答问题使调查样本减少而影响精度，在进行等距抽样时，抽够了规定的样本量之后，继续按原间距再抽取若干样本，做为后备调查样本。
二、抽样方法与操作
本方案采用了与样本规模成比例的不等概率放回抽样和等距（系统）抽样方法，它们的操作步骤如下：
（一）等距（系统）抽样
等距（系统）抽样是在居（村）委会中抽取被调查户的抽样方法。
1.根据课题组以随机抽样原则确定的居（村）委会的名单，在抽中的居委会索取户口清单，并在清单上自1开始顺序编号。
2.在编号后的清单上做等距抽样。首先确定每一居（村）委会的抽样间距。它等于居（村）委会户口总数除以预定的样本数，不能整除取整数或四舍五入。如某居（村）委会的户口总数为350，预定的样本数为34，则间隔为350/ 34=10.3，即每隔10户抽一户。
3.在确定抽样间隔后，还必须随机地确定抽样的起始位置。具体方法是在1至第一个间隔距离之间，如上例中的0～10内，使用随机数表、骰子或计算机的伪随机数，产生一个随机数， 假如这个数为3，则清单上的第3户便被选入样本，然后每10户抽一户，即清单上第3，23，33， …将被选入样本。
（二）与样本规模成比例的不等概率放回抽样（PPS抽样）
本方案从第一阶抽取初级单位（城市）到第四阶抽取居委会，都采用PPS抽样方法。具体的步骤是：
1.建立抽样框。PPS抽样的抽样框除了要有抽样单位的名单之外，还要有辅助变量——抽样单位的人口数。
2.根据抽样框中的人口数计算抽样单位的人口累计值。
3.在0—累计值内，使用随机数表、骰子或计算机的伪随机数，产生一个随机数。
4.判断这个随机数在哪两个累计值之间，如1034825在西岗区的累计值702045和沙河口区的累计值之间，那么大的累计值对应的抽样单位被抽中，沙河口区是被抽中的第一个样本。
5.如果要抽取n个样本，那么就操作步骤3和4n次，得到n个样本。
6.如果某一单位被重复抽中，重复抽中的操作取消，重新再操作步骤3和4，抽取样本单位。
三、 目标量估计方法
（一）在居委（村）会中采用等距（系统）抽样方法， 目标量估计公式与简单随机抽样的公式相同，为
（二）第一至四阶PPS抽样的估计方法，应用Hansen-Hurwitz估计量，公式为
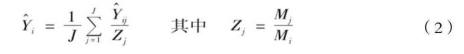
因为在多阶PPS抽样中，公式中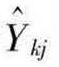
j亦为下一阶样本单位的总量估计，这个总量估计也是用公式（2）计算的。在各阶样本单位等量分配时，最后抽取的样本户概率是相等的，样本可以自加权，样本指标即等于目标量的估计。所以城市，大城市层及中小城市层子总体的估计公式分别为
大城市与中小城市的样本是按人口比例分配的，因此，总体的总量估计为层总量之和
在公式（1）到（5）中，h， i， j， k， l， g分别为层、市、区、街道、居委会和调查样本的下标，H为层数，I为样本城市个数，J为样本区个数，K为样本街道个数，L为样本居（村）委会个数，G为居（村）委会中的样本数。M为人口数（严格地讲，应为20～65岁的人口数）。
四、误差分析
（一）抽样误差
在复杂抽样调查中， 目标量估计精度并不都能事先利用某一公式计算，要在调查之后根据实际调查数据利用与抽样方法相对应的计算公式，计算目标估计量的方差估计与精度。Hansen-Hurwitz估计量的方差的估计公式为
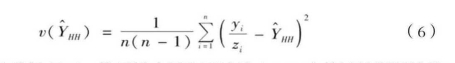
在对调查精度要求不是很严格的情况下，常用样本量和设计效应deff来估计抽样误差的水平。设计效应deff是用来评价复杂抽样设计方案优劣的指标，公式为：
一般复杂抽样设计的deff经验数据在2～4之间。
此调查的调查项目大多数是定性变量， 目标量是总体比例型的，记作P。对于比例型目标量，其样本量与最大允许误差的关系在简单随机抽样下公式为
其中，Δ为绝对误差，在样本量设计时也称为最大允许误差或抽样极限误差。t为概率度，也是正态分布双侧分位数，在一定的概率保证程（置信水平下）有不同的数值。
目标量估计精度公式为
其中，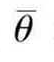
为目标量估计。引用了设计效应deff这个指标，就可以利用以上简单随机抽样的公式（7）来估计调查方案的抽样误差。
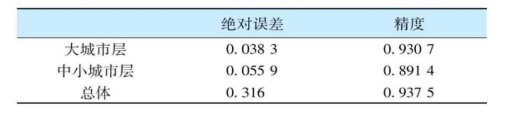
由于目标量比例估计P事先并不知道，并且各项指标的P值是不相同的，为此我们以性别比例指标为例，在此，我们取概率保证程度为95%，则 t=2，取deff为3。大城市层、中小城市层和总体的样本量分别为2040， 960和3000，它们的性别比例指标分别为50.22%， 51.48%和50.62%，那么它们性别指标的抽样误差分别如表A-3所示。
表A-3 性别指标抽样误差
（二）非抽样误差
抽样调查中的非抽样误差主要来自三个方面，一来自抽样框，二来自无回答的样本，三来自指标量度误差。例如由问卷设计中各种文字歧义引起的，调查员调查采用的非标准化用语引起的，回答人对问题的理解的差异引起的，数据处理引起的，以及使用后备样本引起的各种误差。这些误差的判定、计算和调整是目前抽样调查中的热点和难点。这里我们仅就由使用替代样本引起的误差进行一些讨论。
抽样调查中我们常常因为研究设计者事先难以预料的原因，如调查对象搬迁、大批外出打工等不得不放弃原抽取的样本，而重新抽取调查对象，即使用替代样本。这时，尽管无回答样本不变，但样本量却扩大了。如果无回答的样本指标分布与扩大了的样本相近，那么就没有大偏差，反之则会产生偏差。为了判断计算由替代样本所引起的偏差，本次调查中的烟台调查记录了无回答样本居民数量和他们的性别年龄，并采用性别比例和40岁以上年龄比例作为判定指标，作为计算由使用替代样本所引起的偏差的指标。
采用替代样本可能出现二种情况，一是替代样本是严格的概率样本。这时，总体的偏差来源于无回答样本。在替代样本是非概率，且无回答样本与替代样本的偏差分布相近的情况下，这时总体近似无偏差，否则总体偏差是无回答样本和替代样本偏差之和。
在第一种情况下，设原设计样本无偏，样本量为n，无回答样本有偏，样本量为n1，替代样本无偏，样本量为n2，使n1=n2，则实际无偏的样本量为n+n2，有回答样本量为n0=n ，那么无回答率为r1=n1/ （n1+n） 。设P为总体性别比例，P0为回答层的性别比例，P1为无回答层的性别比例，设p0是回答层性别比例的无偏估计量，则在性别比例估计中，由于无回答所产生的偏差期望值为
在第二种情况下，设原设计样本无偏，样本量为n，无回答样本有偏，样本量为n1，替代样本有偏，样本量为n2，使n1=n2，则实际样本有偏，样本量为n2+n，有回答样本量为n0=n，那么无回答率与替代率相等为r1=n1/n=n2/n。设P为总体性别比例，P0为回答层的性别比例，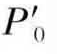
为设计样本回答层的性别比例，P1为无回答层的性别比例，P2为替代层的性别比例。设p0是回答层性别比例的无偏估计量，则在性别比例估计中，由于无回答样本和替代样本所产生的偏差期望值为
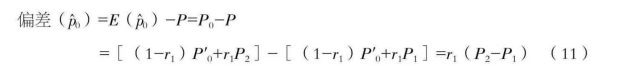
在实际实施调查中，如果替代样本是按概率抽样原则抽取的，就按公式（10）计算非概率抽样的偏差，如果替代样本是由调查员选择的，或按事先设计的某种分布选择的，就按公式（11）计算非概率抽样的偏差。
以烟台市的数据为例，使用公式（10）计算的无回答偏差值见表A-4。
表A-4 烟台市无回答样本引起的性别比例偏差值
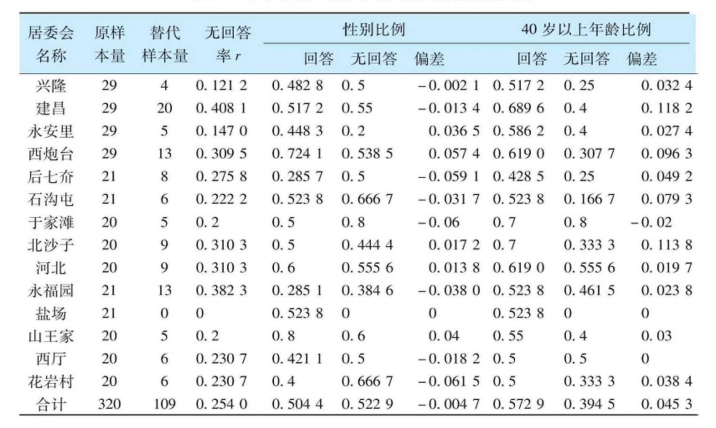
以上数据表明无回答样本引起的性别偏差很小，只有-4‰，在抽样误差的精度范围之内。而40岁以上年龄比的偏差很大，达4.5%，说明在调查中不在场的年轻人居多；同时也不排除，替代样本有偏差，替代样本中40岁以上年龄的样本偏多。
【注释】
[1]作者系中国社会科学院社会学研究所研究员。因篇幅所限，本文已作删节。