10.2.4 完全随机设计
在社会研究中,最简单的双盲实验就是随机抽取若干名对象分成两组,分别接收两种“实验变量”,但是哪个是真正的实验变量,除了研究者之外任何人都不知道,然后进行“后测”,根据测试结果比较实验变量对被实验对象的影响。这样的双盲实验一般采用的是有控制组的事后实验,如果要做前测,有可能使被实验者知道实验的目的。如果一定需要做前测,可以有两种方法:一是把前测的内容隐蔽在测试卷中,不让被实验者知道测试的目的;二是把相隔不久的相类似的测量结果作为前测。按上例,随机选择40名农民工,以文娱活动的名义组织他们观看电影,观看什么电影采用抽签方法(性健康教育电影票和一般电影票各有20张,选择的电影最好对农民工具有同等的吸引力),电影结束后组织他们进行性健康知识认知水平的测试,并进行比较。为了做到双盲,无论是实验的组织者还是被实验对象都不应该让他们知道实验的真正目的,而是以文娱活动的名义组织他们观看电影。如果需要前测的话,可以在看电影前组织他们进行一次综合性的问卷测试,把有关性健康知识的测试内容分散在问卷中,或者在另外一个工地进行一次民工性健康知识的调查,以此作为前测。
完全随机设计可以采用简单随机抽样方法,实验变量可以有几个,但是其中只有一个是真正的实验变量,并按随机方法分配给实验单位,真正的实验变量除了研究者之外任何人都不知道。实验变量之间的差异采用假设检定法(F检验),即方差分析或变异量分析进行确定。
例如,采用图片展示、个别访问或辅导、看录像三种实验方法进行农民工性健康教育,并按随机方法分配到三个建筑工地A、B、C,真正的实验变量是“个别访问或辅导”。经过半个月的实验,测试结果如下(见表10-8) :
表10-8 完全随机设计举例
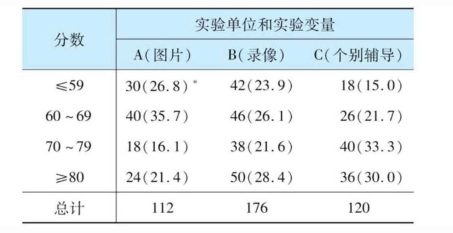
①注:括号内为百分比。
根据比率,似乎个别辅导最有效,但是方差分析显示,F=4.28 >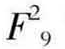 (0.05)=4.26,即在同样的自由度和显著度(0.05)下,F的计算值大于查表所得到的F 临界值(4.26) 。虽然F计算值大于临界值,理论上可以说接受研究假设,拒绝虚无假设,三种实验变量是有差异的,但是差异太小,即使要做推论也要非常小心,比较稳妥的做法还是接受虚无假设,即三种实验变量没有差异。
(0.05)=4.26,即在同样的自由度和显著度(0.05)下,F的计算值大于查表所得到的F 临界值(4.26) 。虽然F计算值大于临界值,理论上可以说接受研究假设,拒绝虚无假设,三种实验变量是有差异的,但是差异太小,即使要做推论也要非常小心,比较稳妥的做法还是接受虚无假设,即三种实验变量没有差异。
