6.2.1 简单随机抽样
简单随机抽样方法亦称为纯随机抽样方法。它是直接从总体中完全随机地抽取样本，是概率抽样的最基本形式。这种抽样方法，并不要求对总体的单位或元素进行排队或分组，可以直接从总体中抽取样本。从理论上来说，简单随机抽样方法最能保证总体中各个单位或元素同等被抽取的机会，因此是最符合概率抽样原则的。
简单随机抽样的具体方法主要有两种，即抽签法和查对随机号码方法。
抽签法就如日常生活中的“摸彩”，事先把总体中每个单位或元素编号，将号码分别写在一张小纸条上，折叠好后放入一个容器里，如盒子、袋子，搅拌后就可以直接从容器里任意抽取，直到抽取完规定的样本数为止。例如，某年级有学生300名，准备抽取50人作为调查对象。按照抽签法，只要把300名学生的姓名编上号码，分别写在300张小纸条上，即编制抽样框；折叠好后放入一个纸盒内，搅拌均匀，然后由专人从纸盒内一张一张抽取50张小纸条，即实施抽样；把抽取的小纸条上的号码与总体的300名学生的号码相对应，找到50名学生的姓名，即为调查样本。接下来还要分析被抽取的50名学生的基本状况，如性别、年龄、学习成绩等，与300名学生情况是否差不多，如果差距较大的话，就要重新抽样，这个步骤即为样本质量评估。
但是，抽签法仅适用于总体规模不大，样本比较小的情况。如果一个总体的人数有5000人，样本数为200人，虽然也可以采用抽签法，但是工作量就比较大。因此，大多数情况下采用查对随机数表的方法[4]。随机数表也称为乱数表（见本书附录B） ，表中数值的排列都是随机生成的，没有任何规律。查对随机数表抽取样本的步骤如下：
（1）在界定总体的基础上，编制抽样框，其中包括给总体每个成员编上号码。
（2）按照总体规模的位数，在随机数表中查对相同的位数。例如总体有5000人，就是4位数，我们就在随机数表中从任意4位数开始查对。
（3）在随机数表中由上到下或从左到右抽样，只要小于或等于总体规模数的数值就是样本号码，直到抽满规定的样本数为止。
（4）把抽取出来的样本号码与抽样框中的名单相对照，与样本号码对应的单位名或个人姓名就是样本。
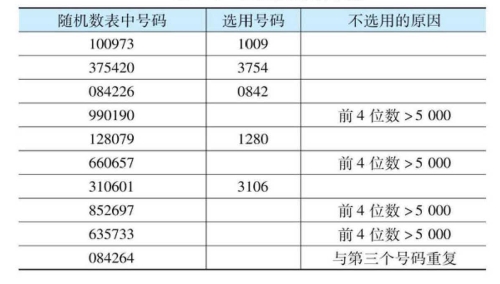
如果我们在一个5000人的总体中抽取200人作为样本，在编制好抽样框后，就可以在随机数表中直接抽样。表6-1就是随机数表的节选，我们可以按任意方向在表中取4位数，如果是从左到右取前4位数，被抽取的样本号码是：1009， 3754， 0842， 1280， 3106（参见表6-1） ；如果取后面4位数，被抽取的样本号码是：0973， 4226， 0190， 0657， 0601， 2697， 4264；也可以从第二个数字开始取4位数，被抽取的样本号码是：0097， 2807， 1060， 3573。需要注意的是，在一次抽样中，只能选择一种标准确定位数，不能一会儿取前面的4位数，一会儿取后面的4位数，一会儿取中间的4位数。
在简单随机抽样中，重复抽样（回置抽样）和不重复抽样（不回置抽样）是一个需要讨论的问题，即总体的单位或元素能否被重复抽取。如果在总体所含的300个学生中，抽取50名学生，可能会发生某些学生被重复抽到。假如有10名学生被重复抽到，按50个样本计算，其中的10名是重复的，实际调查的学生数是40名，其中10名作为重复样本计算，即一个样本作为两个调查对象，仍然是50名学生。但是，这样会给样本的代表性带来很大影响。这种方法就是重复抽样或回置抽样。如果遇到重复的号码就跳过，一直抽取到50个样本为止，其中被跳过的重复号码，即重复对象有10名，虽然实际抽取的样本或次数就是60名（次），但是10名重复对象被舍去后，实际的调查对象还是50名。这种方法就是不重复抽样或不回置抽样。两种方法如何取舍？以笔者所见，主要决定于抽样比率或概率的变化。在本例中，规定的样本是50名学生，抽样比率是：
但是，采用重复抽样的话要承受由此而产生的抽样误差偏大的风险。如果采取不重复抽样方法，由于实际抽取的样本或次数是60名（次），虽然实际调查样本为50名，但是抽样比率是：
因此，已经明显改变了原来的抽样比率，即抽样概率。
表6-1 随机数表抽样节选
如果在5000名学生组成的总体中抽取200名学生作为样本，抽样比率或概率为
假设其中10名是重复样本，实际抽取的样本数或次数是210名，由于10名重复的调查对象被舍去，实际调查的样本数还是200名。虽然抽样比率或概率为
抽样概率发生了变化，但基本上可以忽略不计。如果在总体规模很大，样本相对较小的情况下，不重复抽样可能带来的概率变化是微不足道的。设想一下，若在一个500万人口的城市中抽取1000名样本，即使其中有100名重复样本被舍弃，实际抽样次数或样本数是1100名（即调查样本仍为1000名），对于500万人口的总体来说，1000名和1100名样本对于概率产生的影响是很小的（分别为0.0002和0.00022） ，是可以忽略不计的。
实际上，重复抽样和不重复抽样关系到抽样的独立性，即在一个规定的总体中，任何一个单位或元素的抽取都不能影响到其他单位或元素的抽取。由于调查研究的总体规模都比较大，抽样比率都比较小，即使采用不重复抽样的方法，对概率的影响也很小。因此，抽样调查一般采用不重复抽样方法。但在抽样比率或概率较大情况下，比较稳妥的方法是经过多次抽样获得几组样本，选择一个没有重复对象或重复对象较少的样本。