第五题

第五题

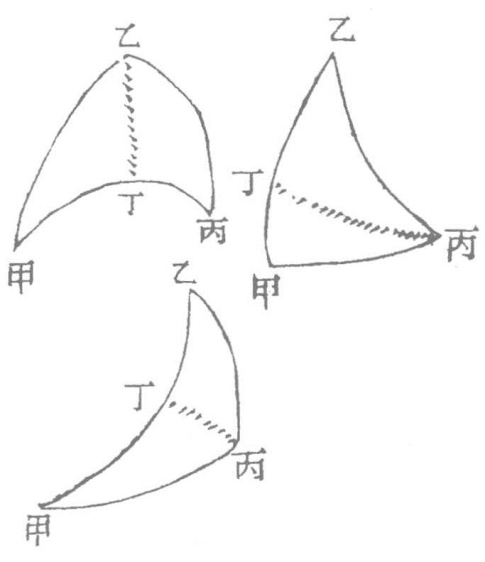
设：甲乙丙形，有乙、丙二角，有乙丙弧在二角之间，求甲角及余弧。

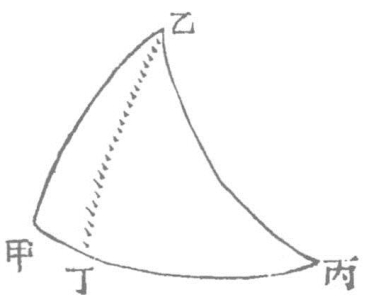
如图，乙甲丙形，有乙角、丙角，有乙丙弧，求甲角及乙甲弧、甲丙弧。法先作乙丁虚线，分本形为乙丁丙，乙丁甲相倚两正角形入算。

先求乙丁垂弧法：

以第一术之正理求之。

一率半径，

二率乙丙弧正弦，

三率丙角正弦，

四率乙丁弧正弦。

检表得乙丁垂弧。

次求乙丁丙形之乙分角法：

以第三术之反理求之。

一率乙丙弧正切，

二率乙丁弧正切，

三率半径，

四率乙分角余弦。

检表得乙丁丙形之乙分角度。

次求乙丁甲形之乙分角法：

以乙丁丙形之乙分角減乙全角，余为乙丁甲形之乙分角。

次求乙甲弧法：

以第三术之正理求之。

一率乙分角余弦，

二率半径，

三率乙丁弧正切，

四率乙甲弧正切。

检表得乙甲弧度。

次求甲丙弧法：

以第一术之正理求之。

一率丙角正弦，

二率乙甲弧正弦，

三率乙角正弦，

四率甲丙弧正弦。

检表得甲丙弧度。

末求甲角法：

以第一术之反理求之。

一率乙甲弧正弦，

二率丙角正弦，

三率乙丙弧正弦，

四率甲角正弦。

检表得甲角度，

或于丙角作垂线亦同。

若角一钝一锐，即破钝角作垂线，其法并同。

右二角一弧，而弧在两角之闲，不与角对为形内垂弧之第三支（此必未知之角为锐角，则垂弧在形内）。