第二十题

第二十题

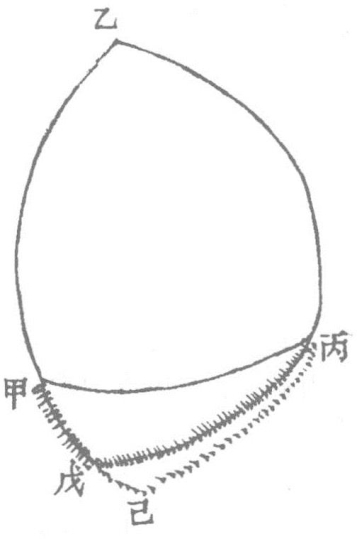
设：乙甲丙形，有丙、甲二钝角，有甲丙弧在二角间，求乙角及余二弧。

如图，乙甲丙形。有甲角、丙角，有甲丙弧，求乙角及乙甲弧、乙丙弧。法于甲戊丙次形作垂弧丙己于形外，补成甲丙己正角形入算。

先求丙己弧法：

以第一术之正理求之。

一率半径，

二率甲丙弧正弦，

三率甲外角正弦，

四率丙己弧正弦。

检表得丙己弧度。

次求次形丙全角法：

以第三术之反理求之。

一率甲丙弧正切，

二率丙己弧正切，

三率半径，

四率丙全角余弦。

检表得丙全角度。

次求次形内丙虚角法：

以丙外角减全角余为丙虚角。

次求丙戊弧法：

以第三术之正理求之。

一率丙虚角余弦，

二率半径，

三率丙己弧正切，

四率丙戊弧正切。

检表得丙戊弧度。

次求乙丙弧法：

以丙戊减半周余为乙丙弧。

次求乙甲弧法：

以第一术之正理求之。

一率甲角正弦，

二率乙丙弧正弦，

三率丙角正弦，

四率乙甲弧正弦。

检表乙甲弧度。

末求乙角法：

以第一术之反理求之。

一率乙甲弧正弦，

二率丙角正弦，

三率甲丙弧正弦，

四率乙角正弦。

检表得乙度。

右两钝角一弧，弧在角间，而于次形外作垂弧，为又法之第六支。