一、基本概念
（一）同质与变异
（1）同质（Homogeneity）
同质是指观察单位或研究对象间具有相同或相近的性质，可根据研究目所规定的纳入和排除标准的条件组合进行限制。例如，研究一种药物治疗高血压的效果时，如果这种药物主要针对原发性高血压的患者，则使用该药物的原发性高血压患者即为同质对象，而其他如肾病引起的高血压患者则不属于同质的范畴。同理，如果治疗高血压的效果受病情的影响，则只能把病情相同的患者视为同质对象。
（2）变异（Variation）
变异是指由于一些未加控制或无法控制甚至不明原因所致的同质的观察单位发生的随机波动。例如，在慢病管理中，年龄相仿、性别相同、身体素质接近的高血压患者，其血压测量值并不相同；再如，同一个人的血压早上测量和中午测量可能差别很大，不同医生对同一个人测量血压时读数也有差别等。变异是事物的个性反映，在生物医学现象中尤为突出，有时要从表现为偶然性的大量数据中，分析出其中必然性的规律。统计学就是解决这一问题的有效工具。
（二）总体与样本
1.总体
总体（Population）是指根据研究目的所确定的同质观察单位的全体。确切地说，总体是同质的所有观察单位某种变量值的集合。总体可分为有限总体和无限总体，其类型随研究问题而定。例如，要探讨某社区的高血压规范管理情况，社区内高血压患者可数，其总体就是有限的；但如果是研究尿激酶治疗心肌梗死的疗效时，总体为接受尿激酶治疗的心肌梗死患者，没做时间和空间限制，则总体是无限的。
2.样本
样本（Sample）是从总体中抽取的部分观察单位，其变量值的集合，通常使用随机抽样的方法得到。样本中所包含的个体数称为样本含量（Sample Size）。例如，调查重庆市2023年所有糖尿病患者的月均医药费用，观察单位是重庆市2023年所有的糖尿病患者，构成目标总体。虽然2023年重庆市糖尿病患者数量有限，是有限总体，但依然很庞大。如果全部调查分析，要耗费大量人财物力。因此，在实际工作中，往往会从该总体中进行抽样，这就要求样本对总体有代表性和可靠性。什么样的样本对研究的目标总体具有好的代表性和可靠性呢？这就要求样本至少具有以下3个特点。
（1）随机抽样获得的样本
随机抽取样本是依据总体规模和抽样框架（Sampling Frame）显示的总体多种结构特征，采取相应方式使每一观察单位都有同等机会被抽取进入样本，这样获得样本称为随机样本（Random Sample）。随机抽样的目的是避免样本对总体的偏性（Bias），增强代表性。
（2）样本中具有足够的研究对象数
医学研究面对的是具有变异性的研究对象和指标，且不同指标测量值变异度大小不一致。这使得医学研究必须面临样本含量的抉择。在一项研究中，研究对象数过少，样本指标数据水平容易偏离总体水平；样本研究对象数过多时，又会带来巨大的成本投入和质量控制的困难。因此，医学科学研究最好是做到“研究对象数的恰当和足够”。其科学含义是指能真实回答提出的研究问题，且具有节约的特点。科学样本含量是在研究者提出一定条件集合（估计或鉴别参数的误差或差别、指标变异度，获得真阳性结果的把握度，以及单、双侧分析和I类错误概率）时，经计算得到的，是有条件的、可以估计的。
对样本含量规模的理解没有一定的严格标准。一般在方法学研究的重复测定中，n＞30即为大样本。而在独立个体的抽样研究中，如指标变异度小，n＞50可算较大样本；若变异度较大，则至少n＞100。此外，应注意样本含量越小，越不容易发现统计量与参数或统计量之间的统计意义的差别。因此，在研究期望获得具有统计学意义时，样本含量是在规定条件下经科学计算的最小样本含量。
（3）样本的结构特征
样本的结构特征特别是那些影响研究结果的结构特征，应与总体的结构特征相一致。虽然随机抽样从宏观方面关注了总体与样本结构特征问题，如人群分布、地区分布、年龄分布等，更细微的问题需给予重点关注。进行动物实验研究时，随机分组要注意品系、性别、体重、健康状态等；研究对象为某病病人群体时，抽样要依据规定的纳入标准和排除标准，分组要注意病情、病期、病型、并发症、年龄及已治疗情况，有时有性别、遗传及其他社会学特征的均衡；对于社区人群而言，主要指性别、年龄、经济收入、文化程度、职业状况、民族、健康状态、所处环境条件和医保状况等。
原则上讲，非随机抽样获得的样本是不能用来对总体特征进行推断的。如果样本含量大，且样本结构特征在主要方面能够反映总体特征时，可考虑非随机样本，但推断时应十分谨慎，且必须认真分析样本可能存在的偏性。
（三）参数与统计量
参数（Parameter）是指描述总体或总体分布特征的统计学指标，是固定不变的常数，往往是未知的，常用希腊字母表示，如总体均数μ。例如，2023重庆市18～45岁男性平均收缩压作为总体均数，由于总体庞大，这个值通常是难以直接测算的。
统计量（Statistic）是指描述样本或样本分布特征的统计学指标，会随着常以拉丁字母表示，如样本均数x。由于个体变异的存在，重复抽样时，样本与样本之间往往不同，故由样本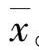
计算的统计量也会有变化，其取值在参数附近波动，可作为参数的估计值。例如，2023年在重庆市某区某三甲医院健康管理中心的体检人群中随机抽取300名18～45岁男性的平均收缩压作为统计量，可以直接测算，并作为重庆市18～45岁男性平均收缩压的估计值。
（四）概率与频率
1.概率
概率（Probability）是描述随机事件发生可能性大小的度量。如果把研究中可能出现的某一结果记为事件A，其发生的概率记为P（A），则其取值范围为0≤P（A）≤1。P（A）的值越接近1，表示事件A出现的可能性越大；P（A）=0表示该事件不可能发生；P（A）=1表示该事件必然发生。在统计学上，把P（A）≤0.05甚至P（A）≤0.01的随机事件定义为小概率事件。由于小概率事件发生的可能性太小，我们认为在一次实际观察或实验中，小概率事件不会发生，这就是小概率原理。小概率原理是统计推断的重要依据。
2.频率
频率（Frequency）指相同的条件下，独立重复进行n次实验，随机事件A出现了f次，则f/n为事件A出现的频率。如调查某地常驻居民高血压的患病率，抽取当地1000名常驻居民，测得其糖尿病患病率为8.2%，即为该地常驻居民患糖尿病这一事件出现的频率。一般随着n逐渐增大，频率f/n始终在一个常数左右微小波动，这个常数就是概率。因此，在实际工作中，只要观察次数足够多，可将频率作为概率的估计值。
（五）误差
误差（Error）泛指实际观测值与客观真实值之间的差异，在统计学上指样本统计量与总体参数之间的差别。根据误差的性质和来源，主要可以分为系统误差（Systematic Error）和随机误差（Random Error）。
系统误差是由一些固定因素产生，如仪器未进行归零校正、标准试剂未校准、测量者读取测量值有固定方向的偏差、研究对象选择不合适、医务人员对疗效标准掌握不准等。系统误差的大小通常恒定或按照一定规律变化，具有明确的方向性，可以通过周密的研究设计和测量过程标准化等措施使之减少或消除。
随机误差包括随机测量误差（Measurement Error）和随机抽样误差（Sampling Error）。随机测量误差指在测量过程中，即使仪器初始状态及标准试剂已经校正，但由于各种偶然因素的影响，也会造成同一测量对象多次测定的结果不完全相同。产生随机测量误差的主要原因是生物体的自然变异和各种不可预知因素。这种误差往往没有固定的大小和方向，但具有一定的统计规律（如服从正态分布）。随机测量误差不可避免，但可以通过多次测量对真实值进行比较准确的估计。
抽样误差是指从总体中随机抽取样本进行研究，所得样本统计量与相应的总体参数往往不相同。这种由于抽样而引起的样本统计量与总体参数间的差异，在统计学上称为抽样误差，抽样误差来源于个体变异。抽样误差可以用统计方法进行分析。一般而言，从同一个总体进行抽样，样本含量越大，则抽样误差越小，样本统计量与总体参数越接近。例如，从某地某年65岁以上参加健康管理的老年人总体中抽取100位作为样本，算得其平均体重（统计量）为62.3kg。这个数不一定恰好等于该地60岁以上老年人体重的总体均数（参数）65.5 kg。两者之间差距就属于抽样误差，由研究对象体重测量值的个体变异引起。
（六）变量类型
变量（Variable）用于表示观察对象在性质、数量和程度等方面的特征，可以取不同数值。变量的观测值称为变量值，也称为资料或数据（Data）。变量有数值变量、分类变量和有序变量3种类型，其对应的数据类型为计量资料、计数资料和等级资料。
1.计量资料（quantitative data）
计量资料也称定量数据。变量的观测结果是数值型的，用来说明研究对象的数量特征，其特点是采用数值的大小衡量变量水平的高低，一般有量纲单位。根据变量取值域，可分为连续型计量资料和离散型计量资料。前者在一定范围内可连续取值，如身高、体重、血压、温度等；后者通常只能取正整数，如家庭子女数、脉搏、白细胞计数等。
2.计数资料
计数资料（Qualitative Data）也称定性数据。变量的观测结果是分类的，反映研究对象的品质特征，通常分类表现为互不相容的类别或属性。例如，按性别将对象分为男性和女性，按血型将对象分为A、B、O、AB型等。
3.等级资料
等级资料（Ordinal Data）也称半定量数据或有序分类数据。变量的观测结果是定性的，但各类别（属性）之间有程度或顺序上的递进。例如，尿糖的化验结果为“-，+，++，+++”，满意度调查的选项按“非常不满意、不满意、一般、满意、非常满意”进行分类等。
统计分析方法的选用与变量类型有着密切关系。根据分析目的，不同类型的变量或数据之间可以进行转换。例如，血红蛋白含量为计量资料，若将其分为正常和异常两个类别，则可以转化为二分类计数资料进行分析；如果将其分为正常、轻度贫血、中度贫血、重度贫血4个等级时，则可以根据需要按照等级资料进行分析。