计数资料统计描述
在健康管理科学中,除前述的计量资料外,还有如阴性和阳性、有效和无效、治愈和未治愈、生存和死亡以及各种疾病分类等计数资料。对这些数据的整理往往是先将研究对象按其性质或特征分类,再分别清点每一类的例数,得到各类别的绝对数。但描述计数资料的数据特征时,通常需要计算相对数(Relative Number)。相对数是两个有关联的绝对数之比,也可以是两个有关联的统计指标之比。相对数的性质取决于其分子和分母的意义,计算相对数的意义主要是把基数化作相等,便于相互比较。例如,某病用A法治疗100人,其中75人有效;用B法治疗150人,其中100人有效。若仅比较两组有效的绝对人数是不恰当的,而通过分别计算其有效率75/100×100%=75%与100/150×100%=66.7%来比较两种方法的疗效才有实际意义。常用的相对数指标有率、构成比和相对比。
(一)率(Rate)
![]()
比例基数可以是100%,或1000/1000等。特别要注意分母中“可能发生”的含义。它是指对某病具有发病危险的人,即暴露人口,而不包括不可能发生某病的人。例如,计算宫颈癌发病率,分母应该是可能发生疾病的女性;又如,计算麻疹疫苗接种率,分母一般为既没患过麻疹又没接种过麻疹的儿童。
在实际运用中,率的计算是简单的,但有以下的率存在混淆使用的情况,特别予以说明。
1.发病率(Incidence Rate,IR)与患病率(Prevalence Rate,PR)

可见,两者在时间、分子和分母要求上均存在差异,故它们的使用不应相同。一般地,发病率是表示发病危险的直接指标,可用于探讨疾病的危险因素,评价疾病防治效果。患病率又称为现患率,用于描述病程较长或发病时间不易明确的疾病的患病情况。
2.死亡率(Mortality Rate,MR)与病死率(Fatality Rate,FR)

死亡率主要反映一个地区或国家其居民总的死亡水平。而病死率旨在说明一种疾病的严重程度,或者对人群的威胁程度。
(二)构成比(Proportion)
若一个事物由若干成分构成,则其中某一成分在整个事物中所占的比例或比重为该成分的构成比。

可见,构成比有其特性:一个事物的构成比之和为1,且各个成分的构成比相互影响。
(三)相对比(Ratio)
相对比是指两个有关联的指标A与B之比,简称比。计算公式为
![]()
式中,A、B两指标可以是绝对数、相对数或平均数。
常见的相对比有男女性别比、医护比、患者和病床数之比,以及流行病学上常用的相对危险度RR值和比数比OR值等。
(四)应用相对数时的注意事项
实际工作中,应用相对数时,需要注意以下4个方面。
1.构成比不能代替率
构成比旨在反映比例或比重;而率则体现某事物发生的频率大小。由表9.6可知,两者截然不同,需要研究者在工作中予以重视。
表9.6 某街道2023年居民高血压的患病情况
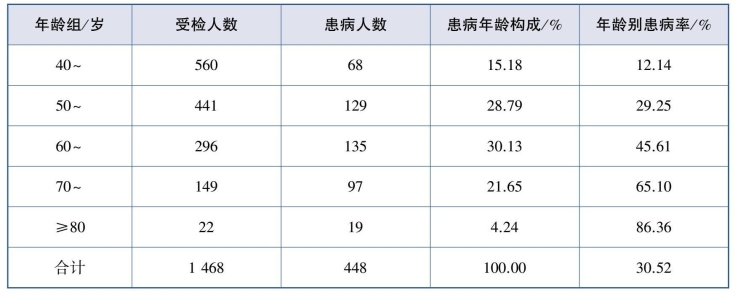
2.分母应足够大
如果样本例数较少,则相对数不够稳定,这时最好使用绝对数直接表示。一般建议,在样本例数大于30例时,即可采用相对数。
3.合并率的正确计算
欲对两组同质的资料,求其合并率(平均率)时,不能简单地由两组分别计算的率相加后求平均,而应该两组分子绝对数之和除以两组分母绝对数之和。
4.资料的可比性
在相对数指标比较时,除研究因素(如不同的药物)不同之外,其余的因素应尽可能相同或相近,主要观察对象其内部结构尽可能相同。若两组资料的年龄、性别、工龄等构成不同,则不能将多个率的数值直接比较大小,而应对其年龄、性别、工龄等构成进行标准化后再作比较。
(五)率的标准化法
如果两组个体的内部构成存在差异,就不能将率的数值直接进行比较。为消除两组个体由于构成不同所带给合计率的影响,则需对率作标准化处理,其方法称为率的标准化法(Standardization)。因此,计算标准化率的目的在于消除内部构成的不同。下面用一个实例来说明如何进行率的标准化。
【例9.12】表9.7为甲、乙两地各年龄组人口数及死亡率,试比较两地死亡率。
【解】由表9.7可见,甲、乙两地总的死亡率比较,甲地(16.19‰)高于乙地(13.90‰)。但各年龄组死亡率显示,各年龄组的死亡率均为甲地低于乙地。不难发现,这两地人口总数虽同为50000人,但其内部的年龄结构却截然不同。甲地老年和儿童人口所占比例大,而乙地青壮年人口居多,这直接导致两地的粗死亡率不具备可比性。为消除内部构成的不同,需进行率的标准化。
表9.7 甲、乙两地各年龄组人口数及死亡率
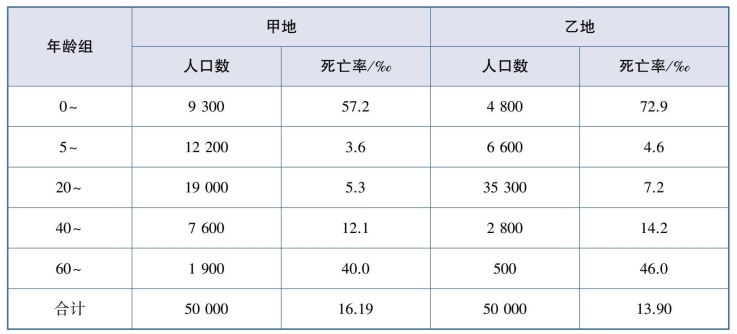
标准化法的关键是选择一个“标准”,在这个共同的“平台”上比较两组资料。“标准”的选择通常有3种做法:
①将两组人口数合并;
②任选两组之一;
③在两组之外另选一个更大的人口群体,作为“标准”。
其中,以第一种最为常用。在统计学中,率的标准化主要有两种方法,分别为直接标准化法和间接标准化法。以下介绍直接标准化法的步骤。
1.选定“标准人口”
例9.12中,将两组人口合并,作为“标准”。其中,甲地n1=50000,乙地n2=50000,n=n1+n2=100000,各个年龄组的标准人口亦随之确定,见表9.8第2列。
2.分别计算在“标准人口”下的预期死亡人数
对于甲地,0~组原有的死亡率为57.2‰,将其应用于“标准人口”中,表示标准人口在原有死亡率下的预期死亡人数,n1p1=14100×57.2/1000=806.52。按此算法,将其余4组的预期死亡人数求出后,得到甲地预期死亡人数之和为∑nipi=806.52+67.68+…+96.00=1383.83(表9.8第4列)。类似地,对于乙地,其预期死亡人数之和为1763.41(表9.8第6列)。
3.分别计算两地的标准化死亡率p′
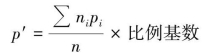
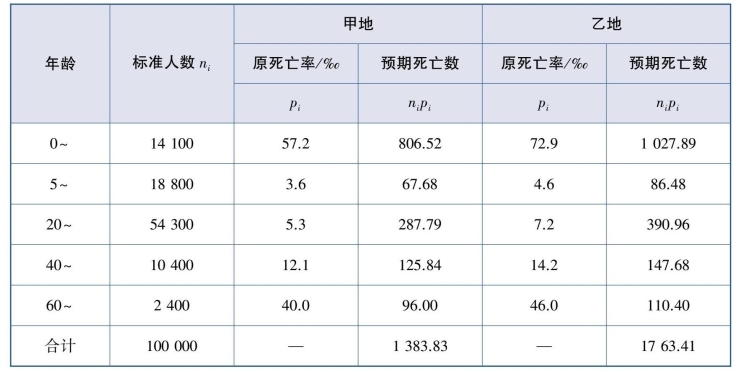
对于甲地,标准化死亡率为
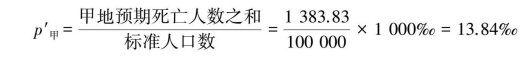
对于乙地,标准化死亡率为
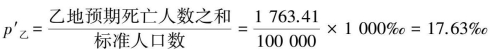
表9.8 直接标化法计算标准化死亡率
※思考题
1.研究人员检测某地居民发汞的基础水平,为汞污染的环境监测积累资料,对象为留住该市一年以上,无明显肝、肾疾病,无汞作业接触史的居民230人,其发汞含量见表9.9。
表9.9 230名居民发汞含量

据此,应该选用什么指标来描述发汞值的集中位置和离散程度?若要计算当地居民发汞值的95%医学参考值范围,应采用什么方法?
2.抽样调查某地60名18岁正常男子生长发育情况,测得其身高均数为178.2cm,标准差为6.8cm;体重均数为63.5kg,标准差为6.8kg。男子身高与体重的变异度相同吗?为什么?
3.为了解某单位职工冠心病的患病情况,对全体职工进行体检后发现,在该单位1290名职工中,患冠心病的有305人,其中女性110人,占36%;男性195人,占64%。因此,认为男性易患冠心病,这种结论是否正确?为什么?
(雷迅)
